第四章:三维变换
补充知识:
旋转矩阵的逆等于它的转置,如果一个矩阵的逆等于它的转置,数学上称为正交矩阵
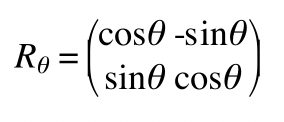
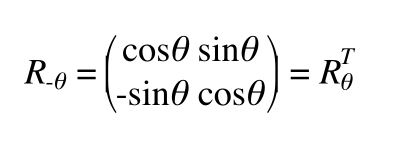
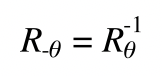
本章知识:
3D 变换
viewing(观测)变换
View(视图)/Camera transformation
Projection(投影) tranformation
- Orthographic(正交)projection
- Perspective(透视)projection
三维变换
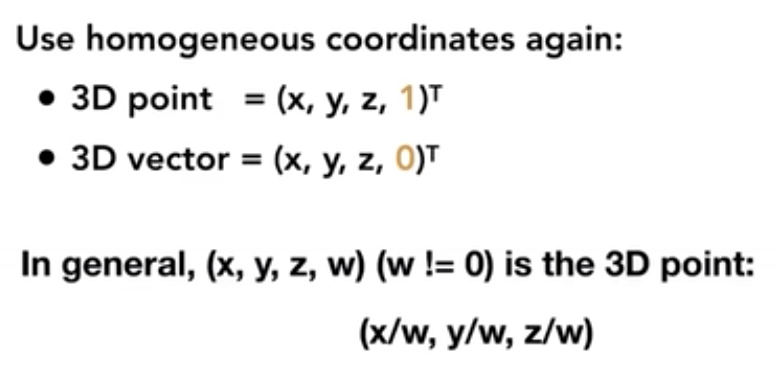

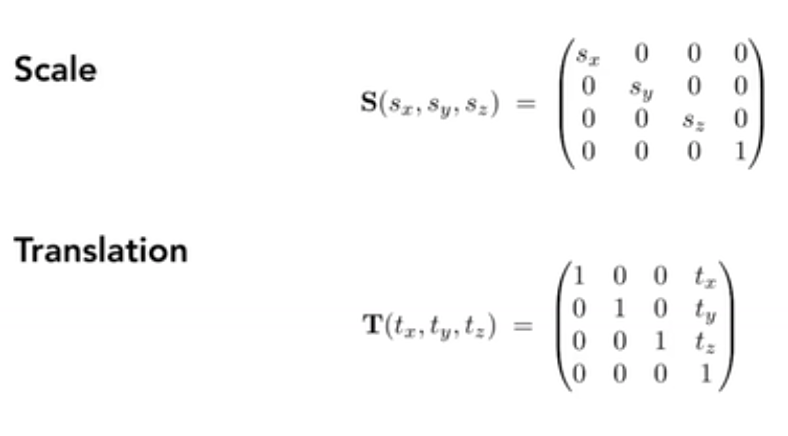
绕坐标轴旋转
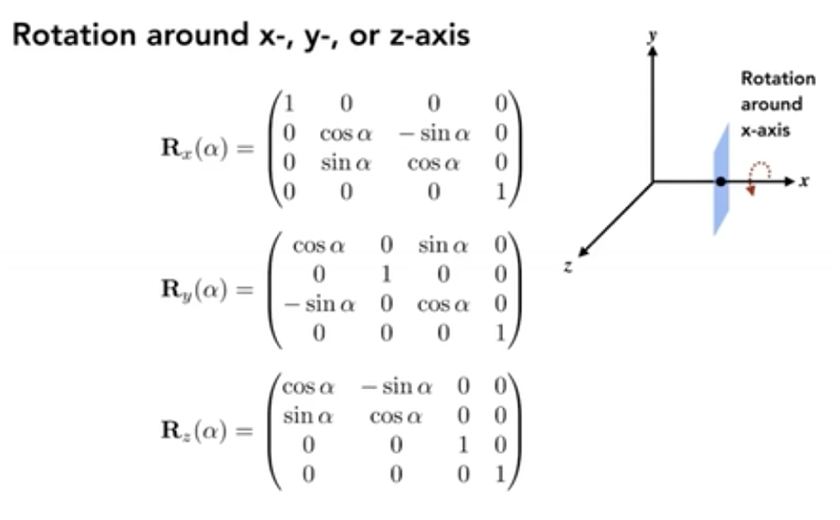
x 和 z 的旋转矩阵和 y 的旋转矩阵是互逆的。
循环对称:x 叉乘 y 得到 z,y 叉乘 z 得到 x,但是得到 y 是要 z 叉乘 x 而不是 x 叉乘 z。
一般旋转
用简单的旋转组合形成复杂的旋转
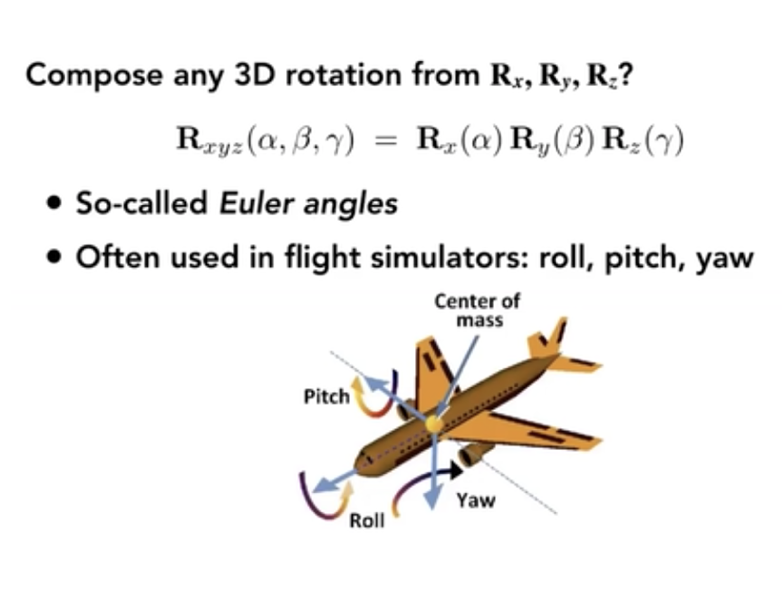
绕任意轴的旋转都可以转换为绕 x、y、z 轴的旋转
罗德里格斯旋转公式(Rodrigues‘ Rotation Formula)

其中 n 是任意旋转轴(可以不经过原点),α 是旋转角
绕任意轴旋转:先平移,让旋转轴位于原点,再旋转,再平移回来。
四元数:解决插值问题。比如二维旋转 20 度的矩阵和旋转 30 度的矩阵相加后除以 2,不等于旋转 25 度的旋转矩阵,需要用到四元数做旋转和旋转间的插值。
Viewing Transform
什么是视图变换
拍照片(MVP 变换)
- 找一个好的位置放置模型(model transformation)
- 找一个好的角度(view tansformation)
- 茄子!(projection transformation)
模型视图变换(Model viewing transformation)
放在哪,往哪看,相机的向上方向(相机怎么摆)
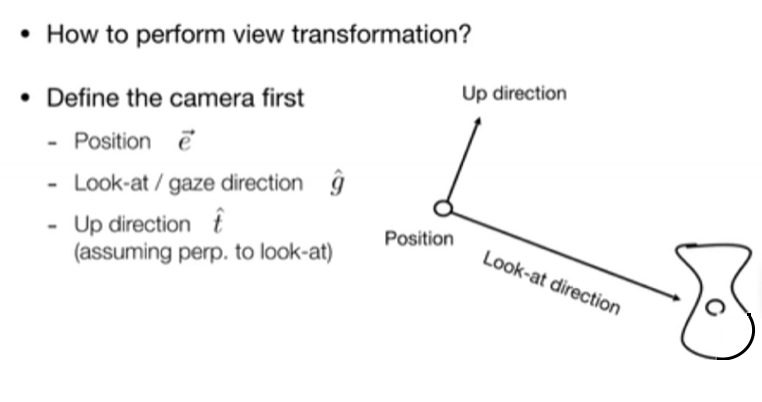
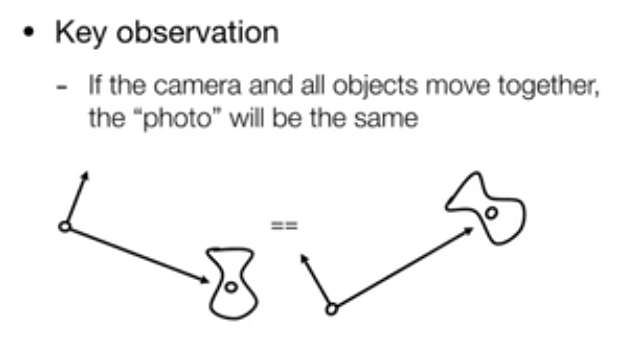
约定俗成:相机放到(0,0,0)位置,向上摆放,沿着-Z 方向看
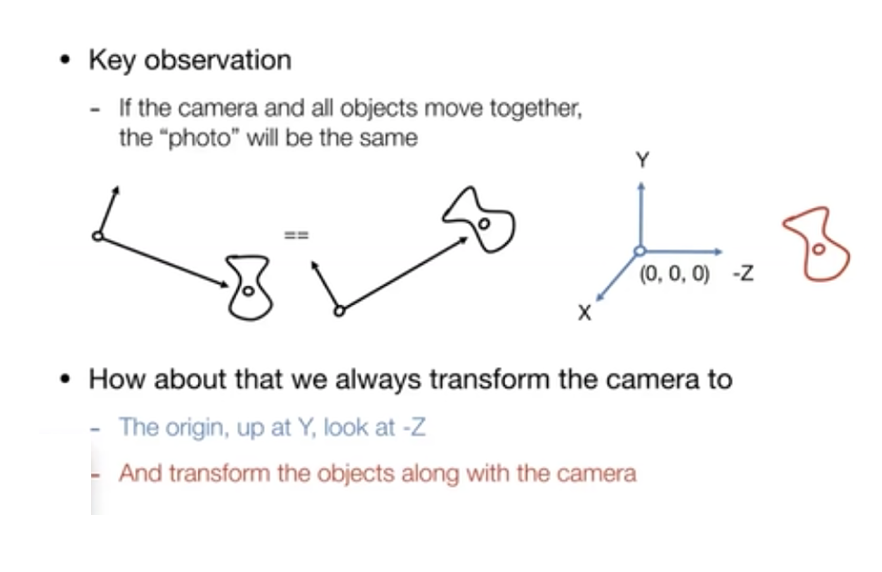
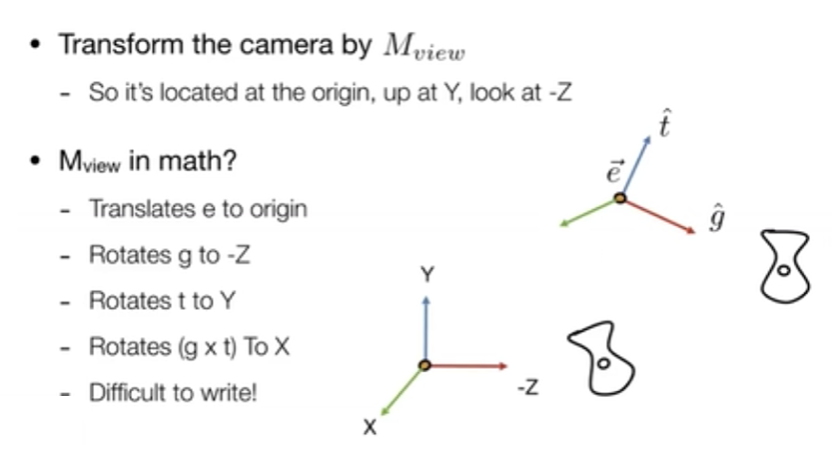
直接旋转角度到坐标轴不好处理,但把坐标轴旋转到某个方向比较容易,所以可以先旋转坐标轴,得到旋转矩阵,再求它的逆。

正交矩阵的逆就是它的转置。
先把中心移动到原点再做旋转的到的变换就是视图变换。相机通过这种变换变换到一个固定位置,其他物体也做一样的变换,保持和相机的相对位置不变。
总结:
任何时候相机和物体做一样的变换
只要相机能移动到规定的位置,那其他物体也会落到需要的位置上
所以模型视图经常一起变换,被称为模型视图变换。
投影变换(Projection TransFormation)
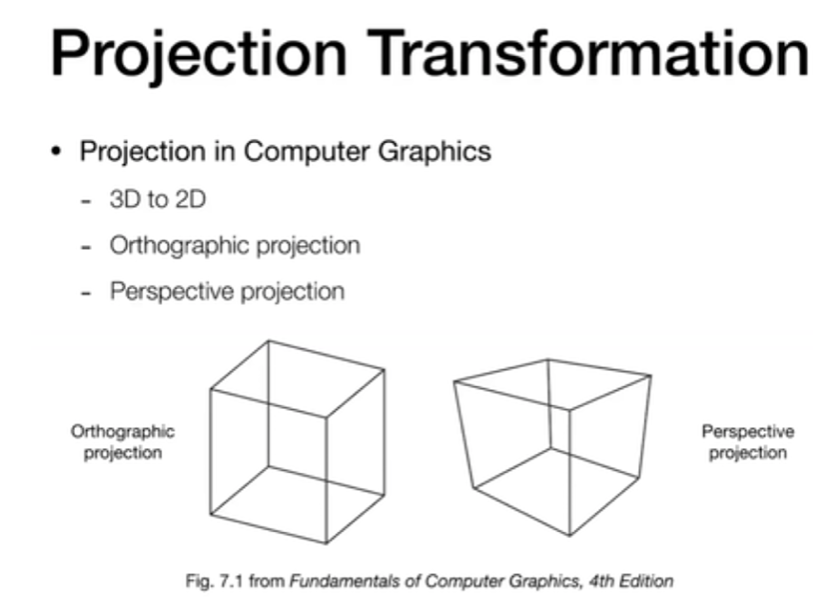
正交投影不会近大远小(鸽子为什么那么大)
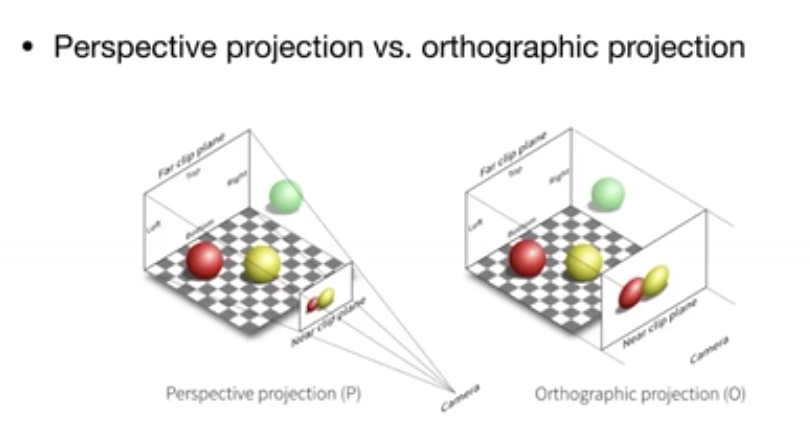
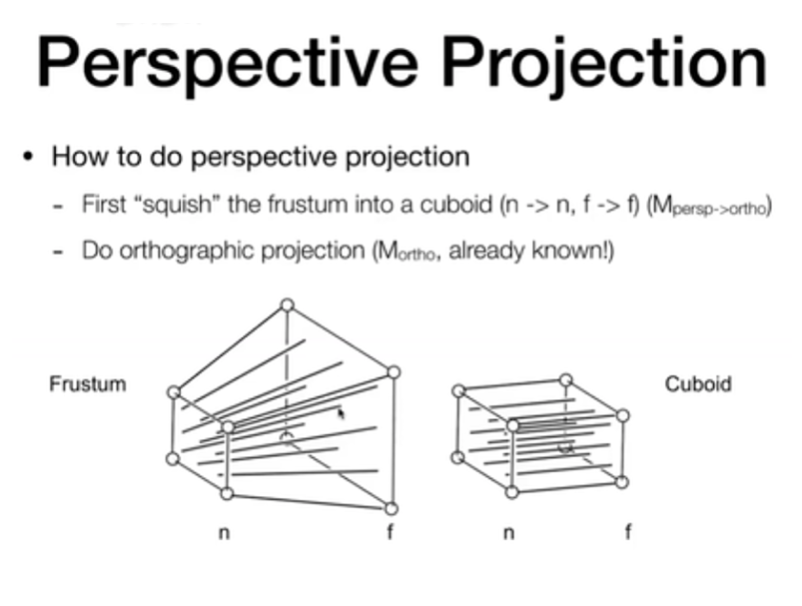
透视投影就是把相机放在空间的一个点,往一个方向连出一个四棱锥,把这个四棱锥某一个深度到另一个深度之间的区域(frustum)都显示出来,显示到近处的平面上
正交投影假设相机离得无限远,这个时候近和远基本是一样的大小
正交投影
简单做法:
相机移到原点,把 z 轴扔掉(怎么区分物体前后后面再说),所有东西都在(x,y)上,然后把范围约束到[-1,1]² 这样的一个矩形里(约定俗成),得到正交投影的结果。
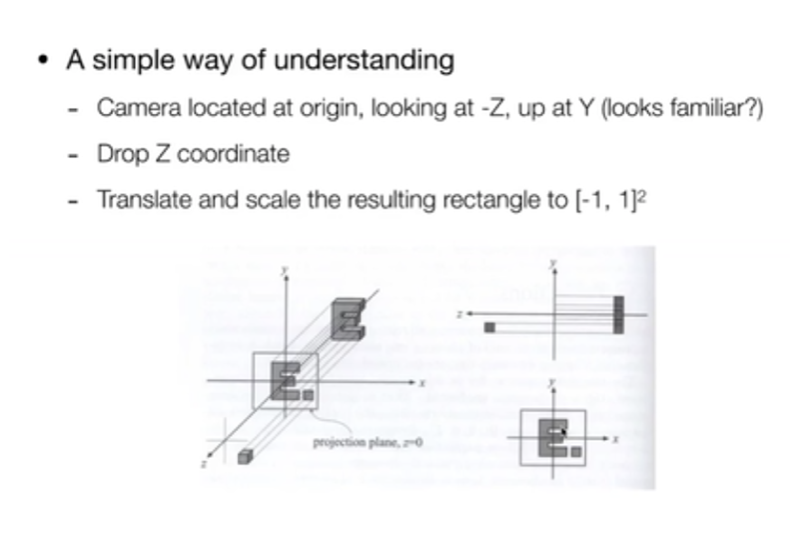
正式的做法:
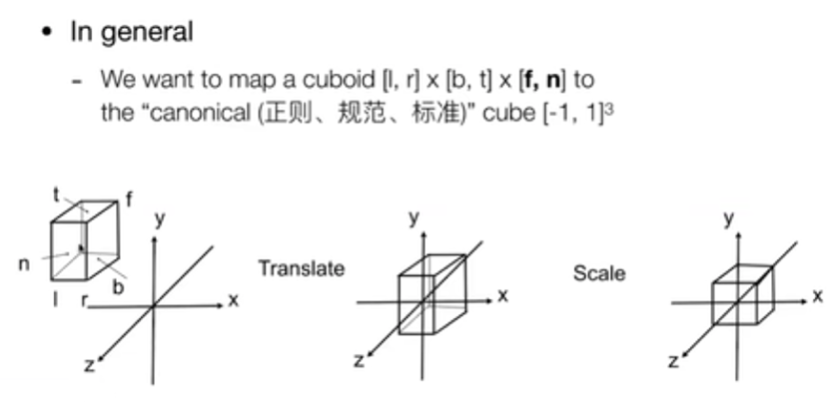
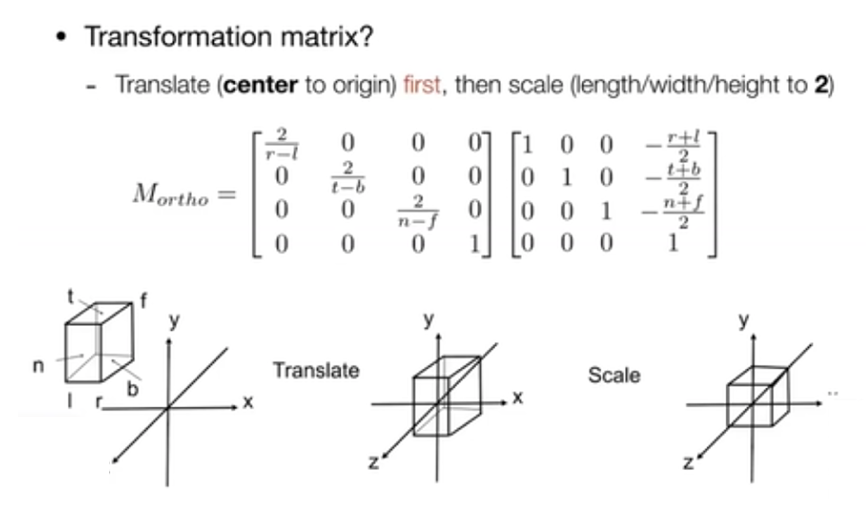
定义一个立方体,映射到一个正则(规范、标准)立方体上。先做平移,再做缩放。
这里用的是右手系,z 方向向外,面离我们更远则 z 值更小,离我们更近则 z 值越大,所以 f 小于 n。所以有一些图形学的 API(比如 OpenGL 从透视空间到裁剪空间,webgl 也是类似)会用左手系,让 z 方向朝里。
透视投影近大远小
平行线不再平行

先把锥体向内挤压成一个立方体,约定近面和远面的 z 轴不变,远面中心点不变,近面大小不变(从透视到正交)。
再做正交投影
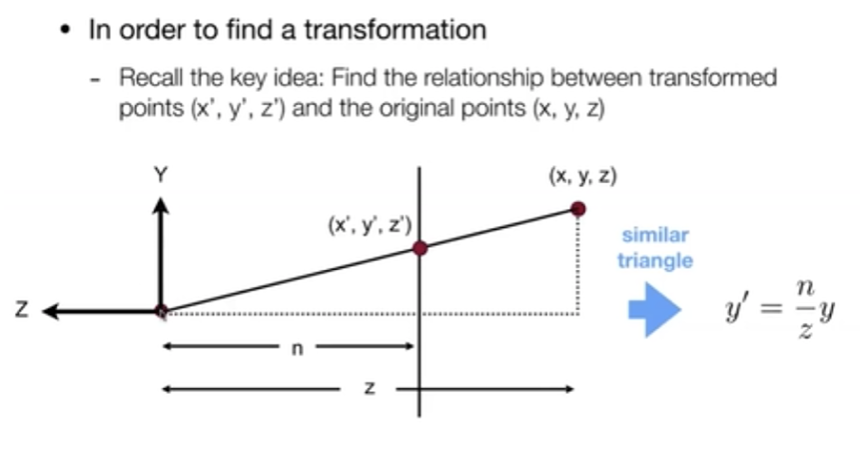
找到远面的 y 和近面的 y’之间的比例关系
齐次坐标里,点矩阵乘一个数字和以前表示的含义一样


近平面的所有点不改变,可以计算出转换矩阵的前两个数字

远平面中心点不变,结合前面近平面的特征,可以计算出剩下两个数字

最终得到透视到正交的转换矩阵

思考:
在近平面和远平面之间的中心点被挤压时,会被推向近平面还是远平面?
对原矩阵做转换后,得到的结果的第四行的值为(0 0 1 0) 和 (x y z 1)相乘后得到:z;
计算 z 转换后的值为(f<z<n)值:z(n+f)-nf,需要除以 z 把最后一位变为 1 后再和原来的 z 比较
求解:(z(n+f) - nf)/z 和 z 的关系,转换为抛物线求解,y = z(n+f)- nf - z² , z 在 n 和 f 之间变化时,有两个解 n 和 f,且抛物线开口向下,即当 z 位于 n 和 f 之间时,其变换后的 z 的绝对值始终大于原来的 z 的绝对值。