第十章：纹理应用、几何

Shading 1&2

• Blinn-Phong 反射模型
• 着色模型/着色频率
• 图形管线
• 纹理映射

Shading 3

• 重心坐标系

• 纹理反走样（MIPMAP）

  • 纹理太小插值，纹理太大 MIPMAP 范围查询

• 纹理应用

纹理应用

纹理：一块内存，可以做不同的范围查询（过滤）
环境光照（环境光映射）

把任何一个方向来的光都记录下来，用纹理描述环境光，用环境光渲染其他物体。假设环境光源都是来自无限远处，不考虑位置。
犹他茶壶

​​​​​​

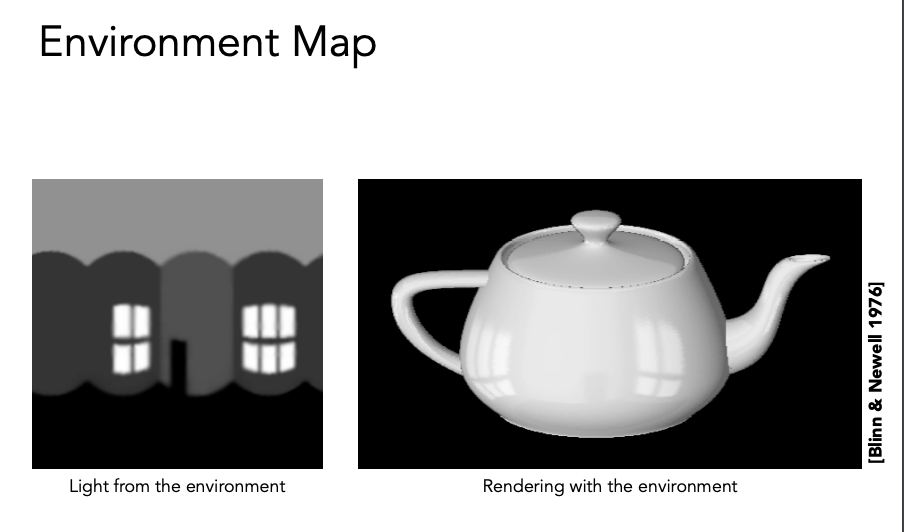
环境光可以记录在球面上，放在不同的方向上记录一个点，再把图展开（就像世界地图）

但这样会在顶部和底部出现扭曲

​​

此时可以假设球外面有一个包围盒，把球心到球表面的连线延长到立方体上，把环境光信息记录在一个立方体上对应的 6 个面上，再把立方体展开：

​​

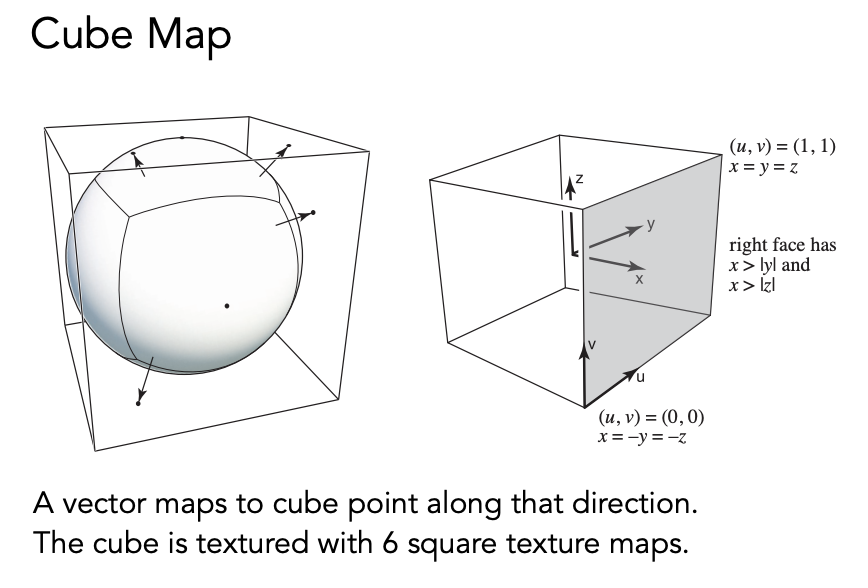
6 个面基本是均匀的，所以不会发生扭曲，但是需要计算方向和面的对应关系。

​​

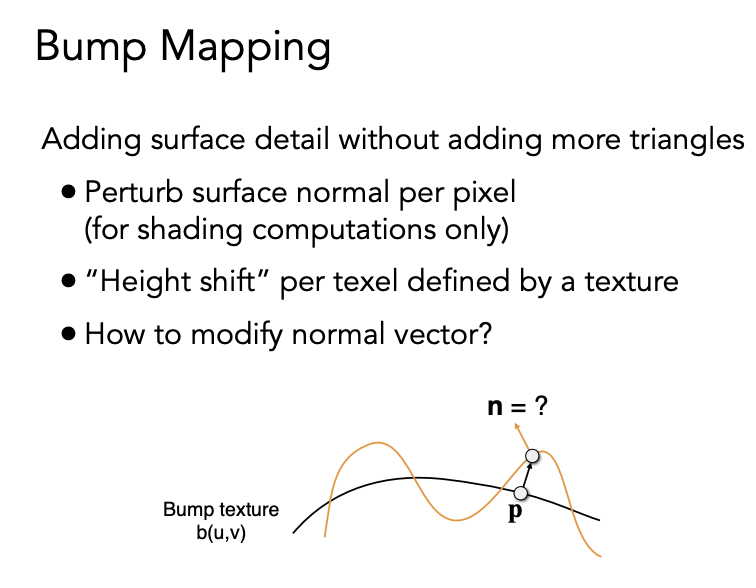
凹凸贴图（法线贴图）
纹理不只是可以表示颜色，也可以表示高度。

可以在不把几何形体变复杂的情况下，定义任意一个点的相对高度，通过相对高度计算出一个假的法线，产生着色上的明暗对比。

​​

对像素做扰动，重新计算法线方向

​​

用相邻两点的高度差除长度，得到切线，通过切线旋转 90 度再算法线

​​

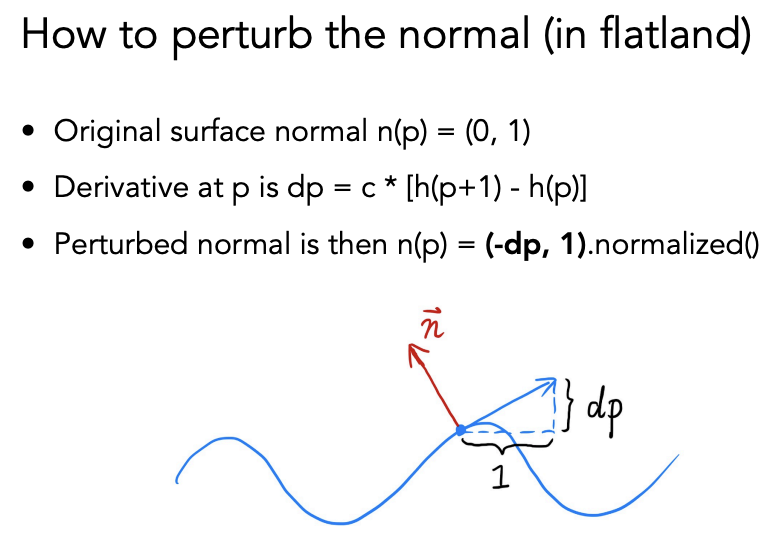
三维情况下需要计算两个方向的切线（假设局部坐标系的法线是（0，0，1））：

​​

位移贴图

凹凸贴图没有真正改变顶点的高度，在边缘和自己的几何会产生自己的阴影的情况下表现失真，这个时候用位移贴图，真正改变三角形顶点的高度。问题就是三角形需要定义得足够细，能跟上纹理定义的频率。

​​

DirectX（动态曲面细分） 先应用一个粗糙一点的模型，应用过程中检测是否满足要求，根据需要把三角形拆得更细做位移贴图。

三维过程噪声

不真正生成纹理图，定义一个三维噪声函数，计算空间中每一个点计算出噪声的值，再通过一些计算得到纹理。

​​

预计算阴影

​​

先计算环境光遮蔽写进纹理图，再把纹理图乘以着色的结果，得到阴影。

三维体积渲染

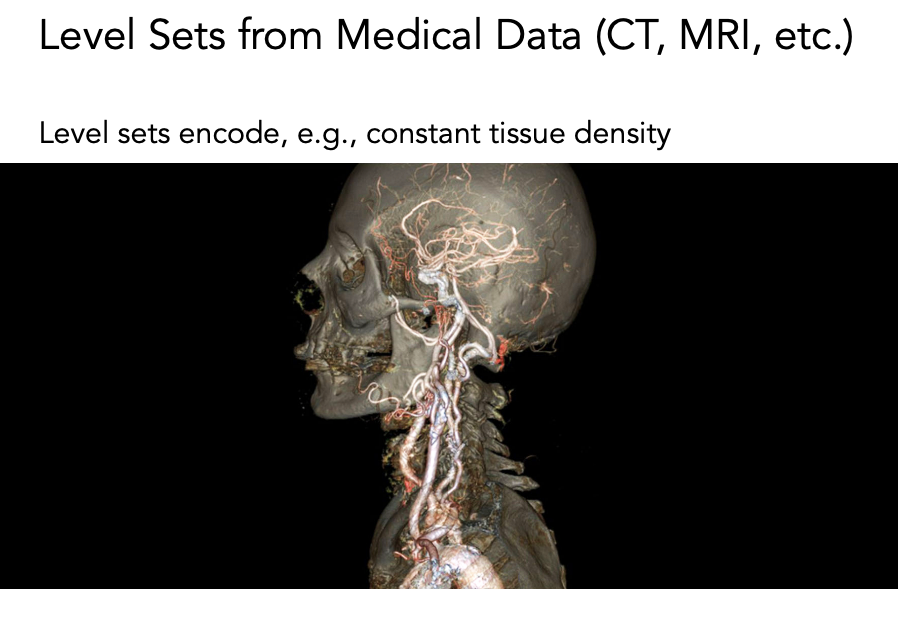
医学成像，核磁共振扫描人体，得到一个密度的三维纹理。

几何

曲线、光滑曲面、齿轮、布料（透明的、纤维）、水的表面形状、城市（大量几何形状）、动物毛发、细胞等等怎么用几何表示。

隐式表示

满足特定关系的一些点表示一个几何，比如一个球体。

f(x,y,z) = 0;

​​

问题：
不好直接看出来表示的几何是什么形状

好处：
可以很快得判断一个点在不在这个几何面上（在几何体内还是外）

显式表示

1.把几何上的面的点直接表示出来

2.通过参数映射定义表面

​​

好处：
很容易找到形状，把(u,v)都算一遍

问题：
不能很快判断一个点是不是在表面上（在几何体内部还是外部）

隐式表示方法：

代数曲面：

​​

可以不只用代数方式来表达：

Constructive Solid Geometry（构造立体几何法，CSG）

用基础的结构体做一些简单运算形成复杂的几何：

​​

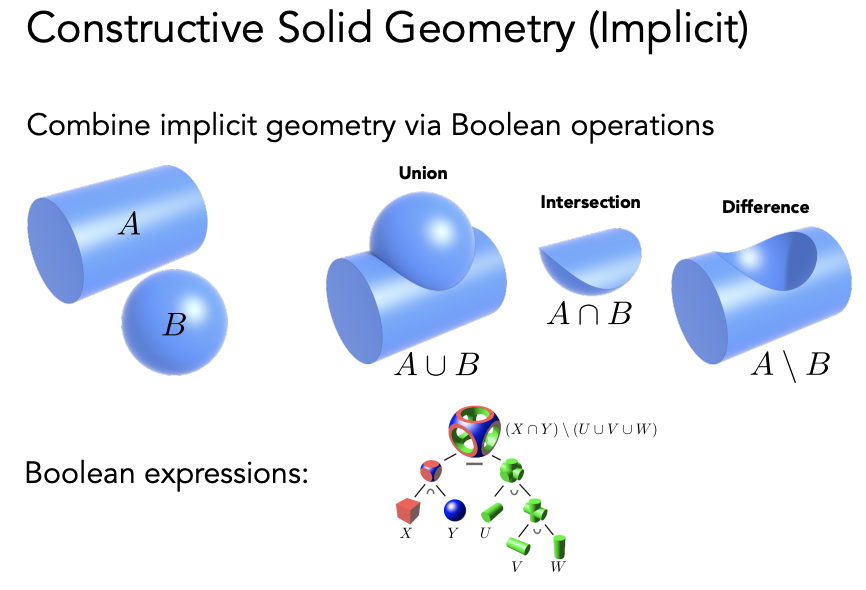
Distance Function（距离函数）

定义任意一个点到这个几何体表面的最近距离

如果距离是正的，说明这个点在物体外部，距离是负的则在物体内部

对两个几何做融合（blend）得到 A→B 从左到右运动的一个中间状态。blend 两个几何的距离函数，其实就是 blend 两个边界。可以通过 blend 出来的结果距离函数，还原出边界（SDF 为 0）。

​​

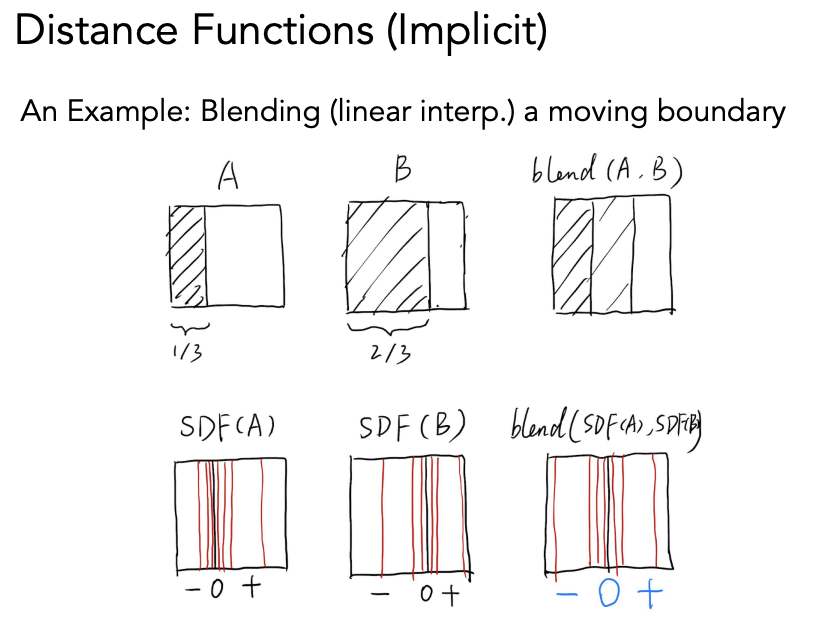
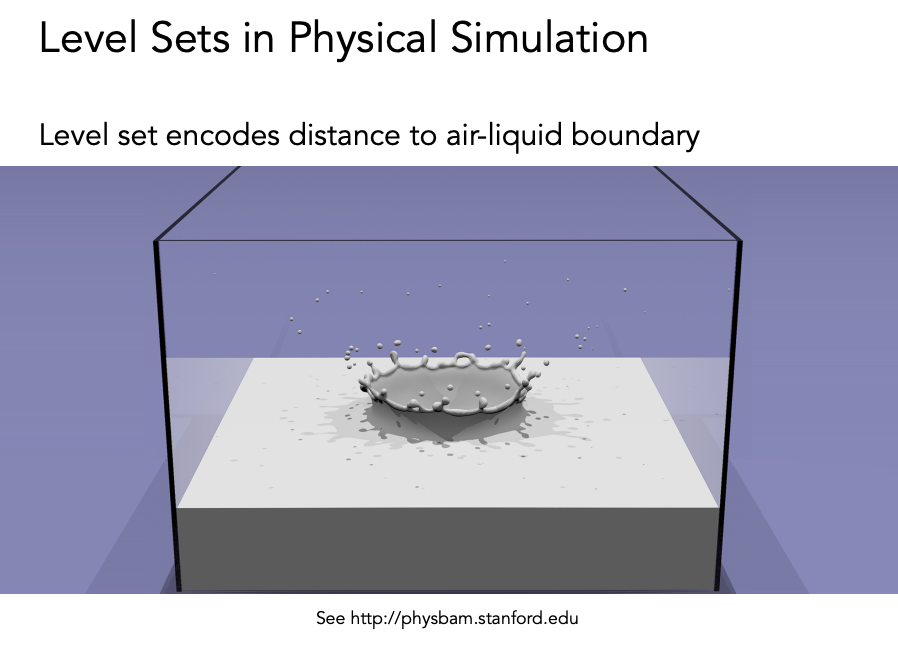
距离函数也可以不写成解析表达式，比如水平集

等高线也是类似

​​

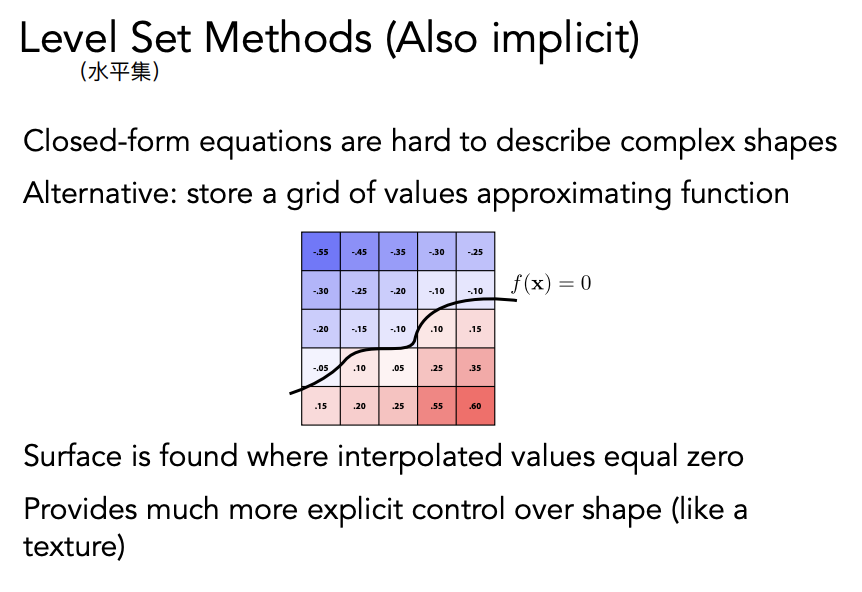
水平集也可以定义在三维上。比如计算三维中 f(x)等于某一个值的所有点，可以得到一个三维空间中的一个表面。
医学扫描

​​

水滴融合

​​

分形

自重复几何

​​

总结：

优点：
隐式函数表示起来比较容易，对存储也比较友好，比较容易判断是否在物体表面。用隐式函数表示的表面很容易对光线求交。严格地表示简单形体，很容易给出准确描述。很适合描述拓扑结构。
缺点：
对复杂的模型很难用一个规则的函数来描述。