第十六章：Ray tracing4 蒙特卡洛路径追踪

Ray tracing4 蒙特卡洛路径追踪

回顾上节课

• 辐射度量学

• 光线传播

  • 反射方程
  • 渲染方程

• 全局光照

• 概率论复习

本节课：

• 简短的 review
• 蒙特卡洛积分
• 路径追踪

review

渲染方程

​​

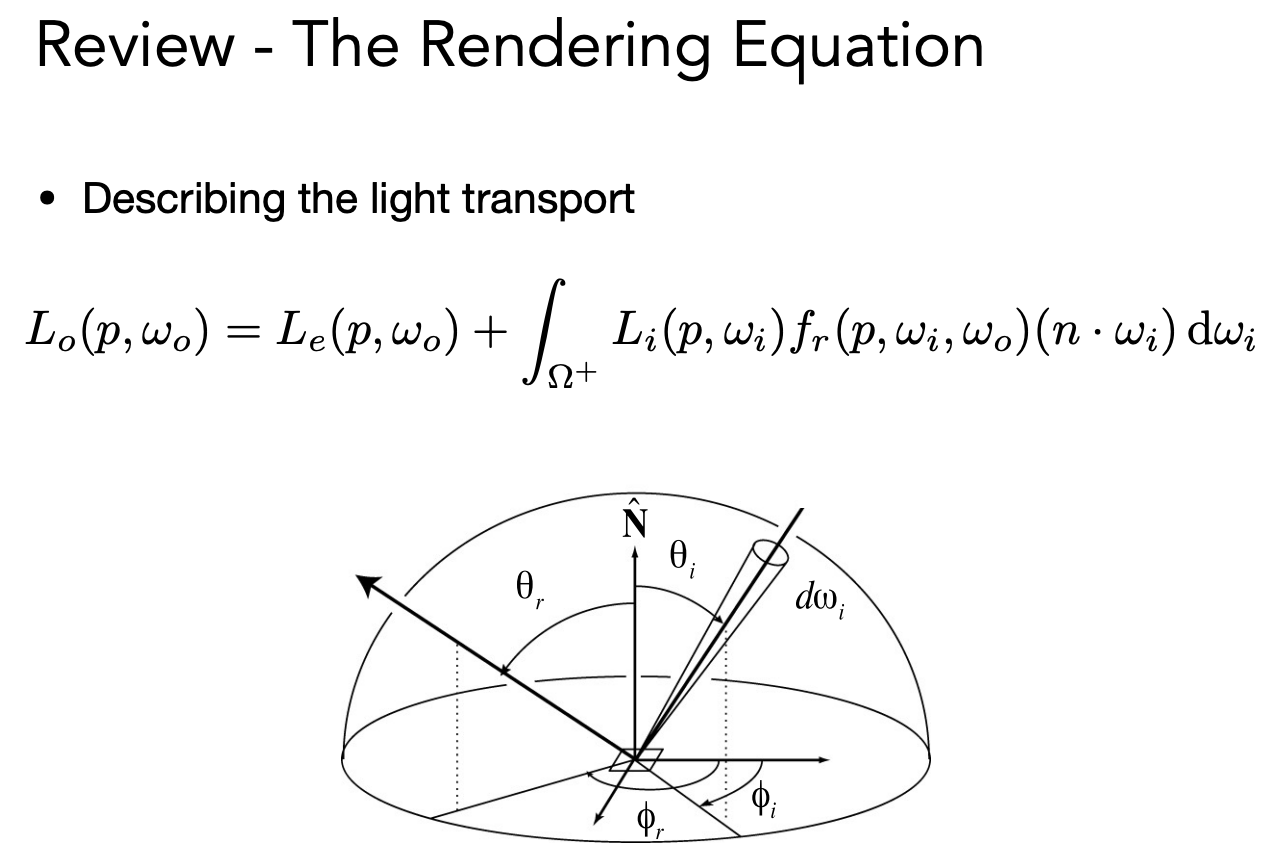
概率论

​​

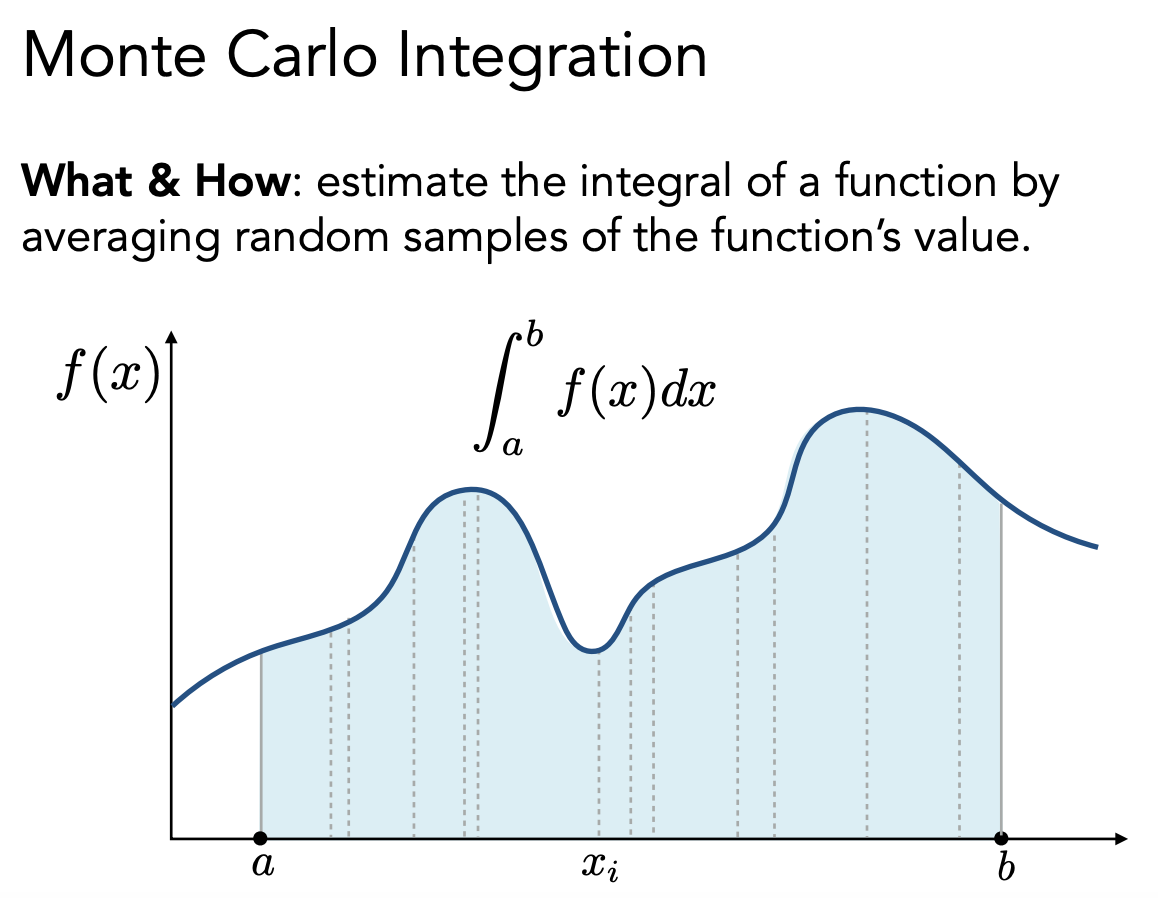
蒙特卡洛积分

在 a、b 随机采样，找到一个 x 对应的 f(x)，用 f(x)从 a 到 b 围出一个矩形。做多次采样，平均采样的结果，得到一个定积分的值。

​​​​

如果是均匀的采样，采样的 PDF 是一个常数：

​​

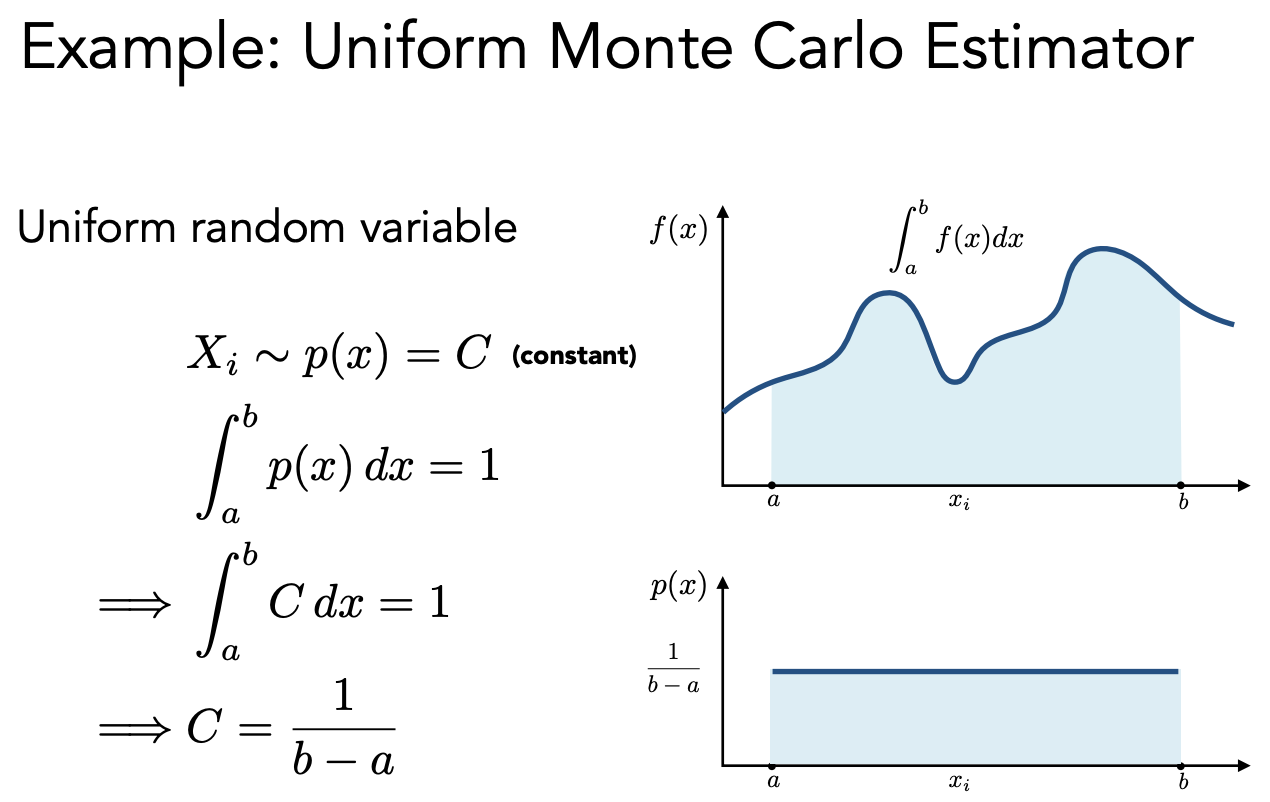
对于均匀的采样，蒙特卡洛的积分结果是：

​​

更通用的情况，不是均匀采样，即 x 的概率密度不是常数，可以通用的表示为：

​​

越多的采样，得到的结果越准。

在 x 上积分，就得在 x 上采样。

Path Tracing

使用 Path Tracing 的原因是 whitted-style ray tracing 有一些不符合真实物理，需要提升这种算法。

​​

1.whitted-style ray tracing 无法处理磨砂材质的反射，他会认为反射光还朝着镜面反射的方向，而这是不对的：

​​
2.whitted-style ray tracing 认为光线打到漫反射到物体就停下来了，但真实的光线还会继续传播

color-bleeding 一个面反射的光到了另一个漫反射的面上，反射面的颜色流到了被反射的面上

​​

whitted-style ray tracing 是错的，但是渲染方程是对的。渲染方程包含了两个问题：

​​

1.对一个半球求解积分

2.递归的问题

可以用蒙特卡洛积分解渲染方程。
考虑一个像素点在直接光照下：

​​​​

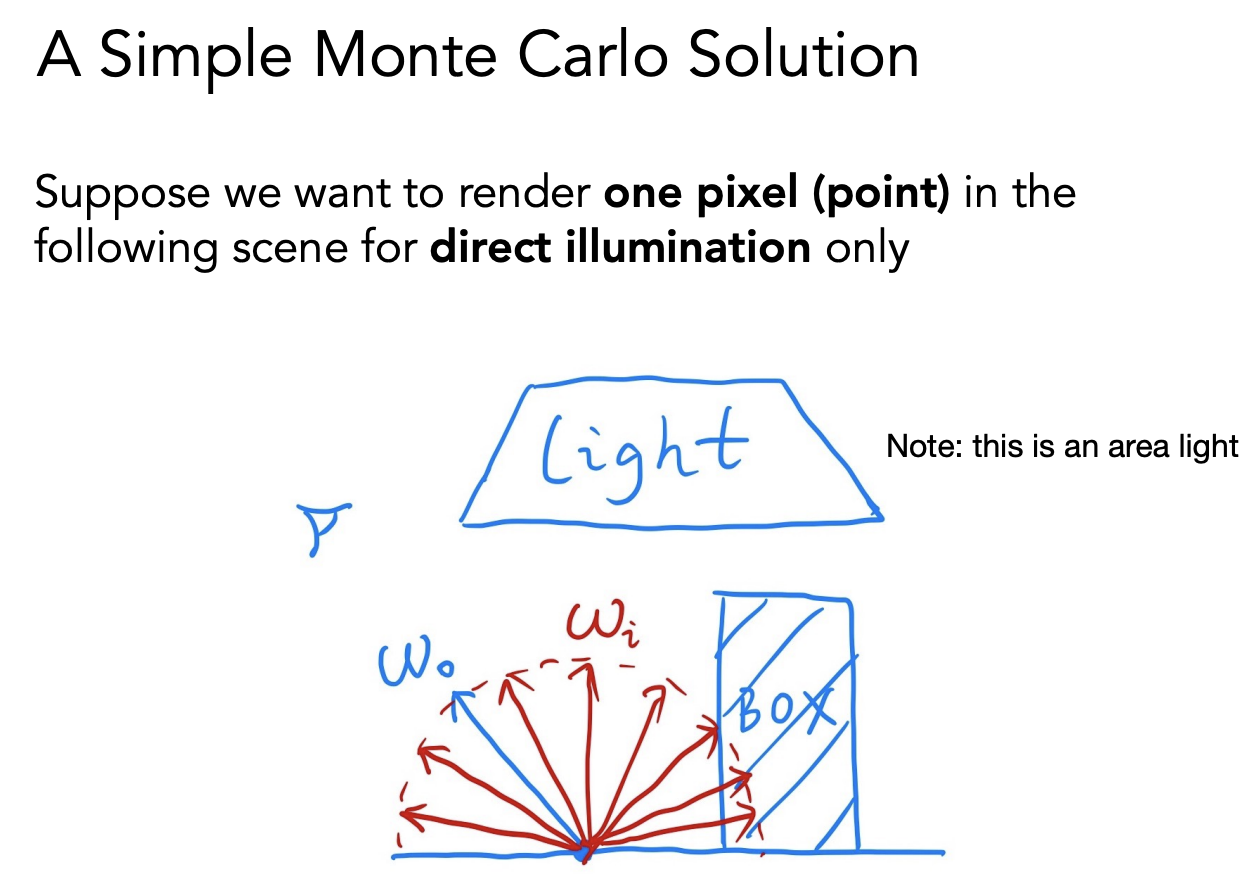
简单的做一个均匀的采样

​​​​

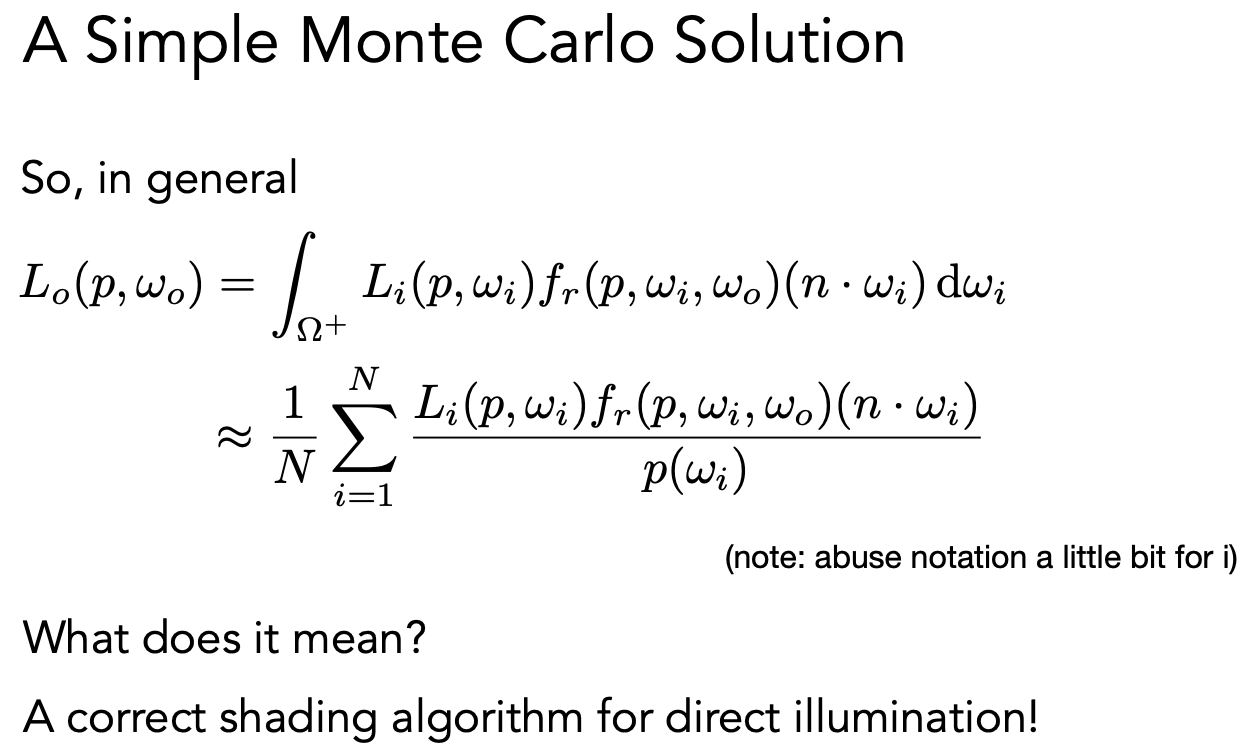
只考虑直接光照：随机选择一个方向从着色点发出一条射线，如果打到了光源，就把光源的贡献算出来，没打到光源的就不算

​​

如果是间接光照，Q 点打到 P 点的光照，就相当于 P 点有一个相机看向 Q 点，在 Q 点算出来的直接光照。

​​

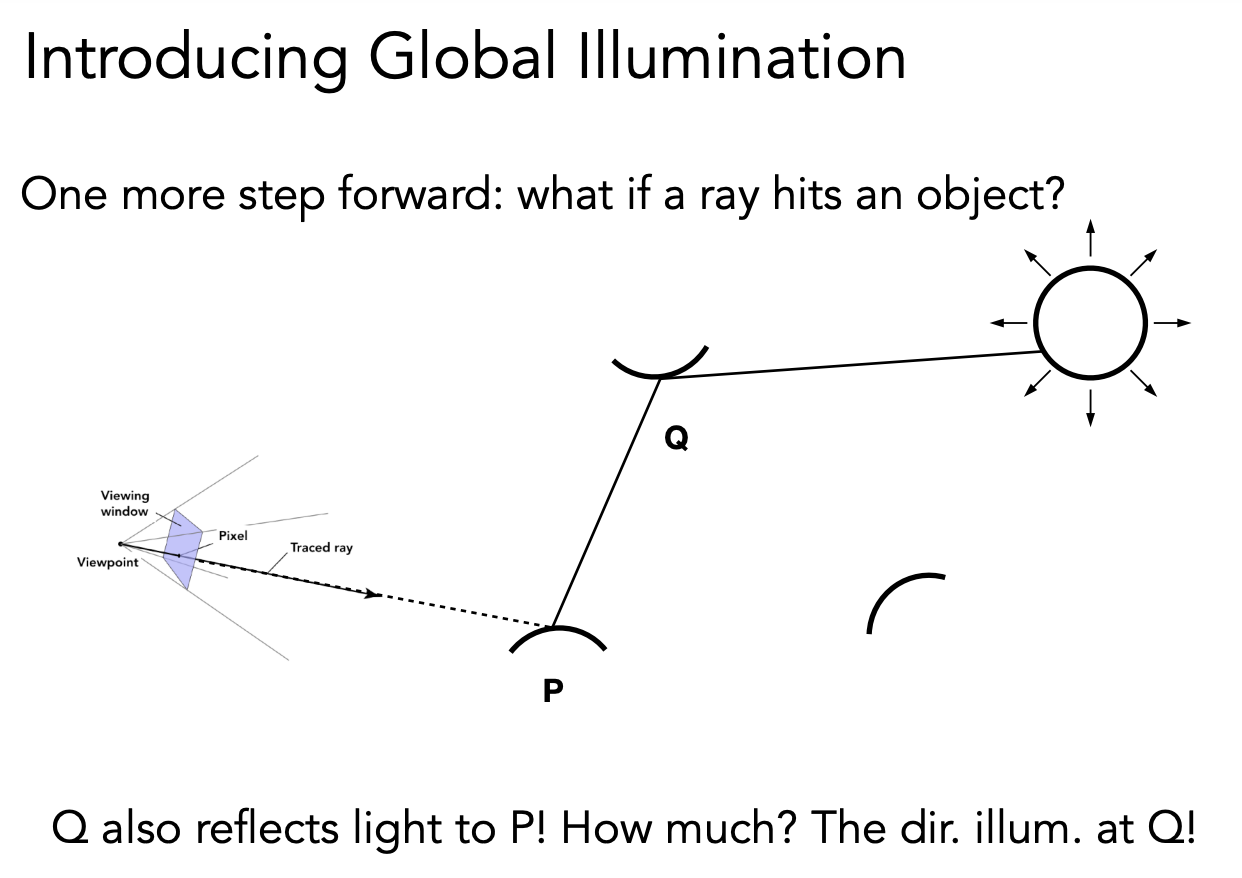
这样可以写出一个递归的算法：

​​

但这样会有一些问题
1.光线的弹射数量会爆炸

​​

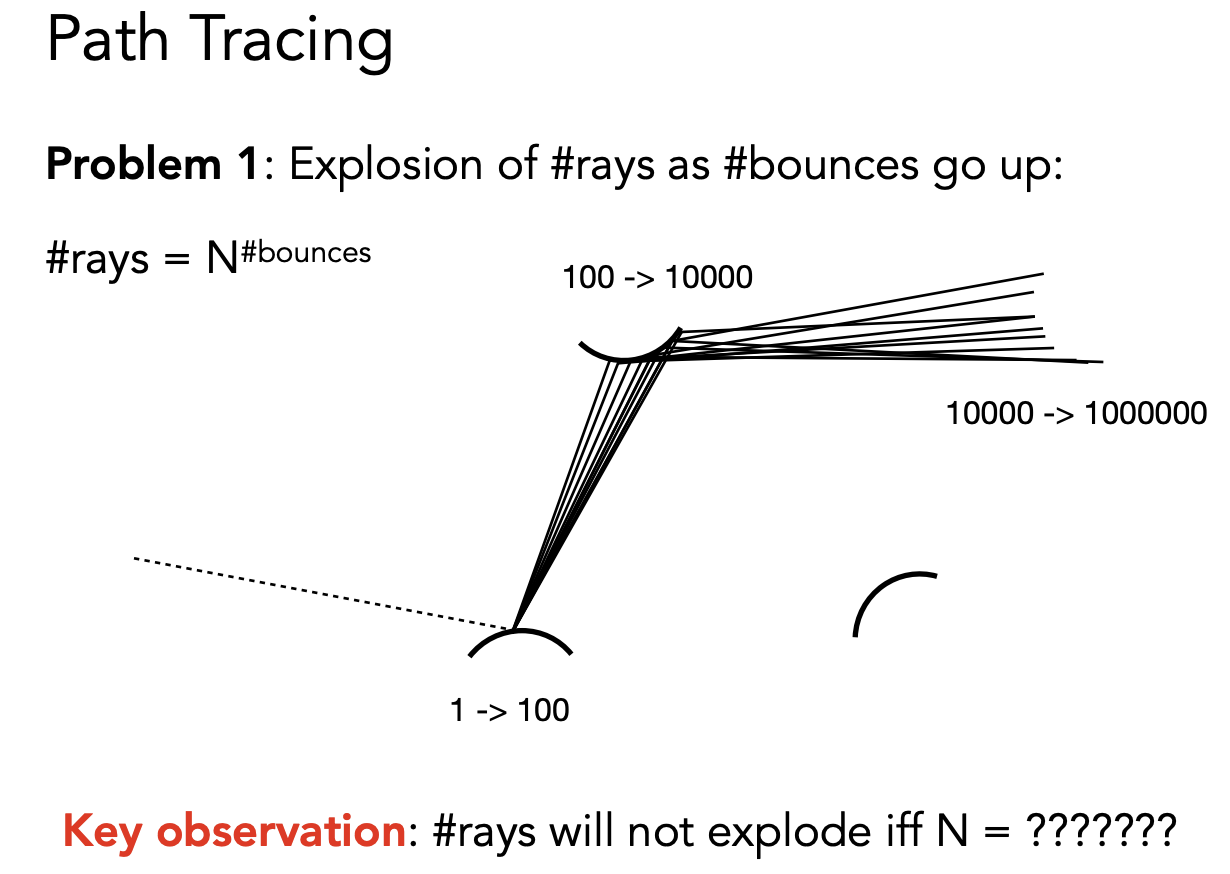
N=1，弹射的数量才不会爆炸。所以，每次只选择一个方向进行采样，这个就叫做路径追踪：

​​

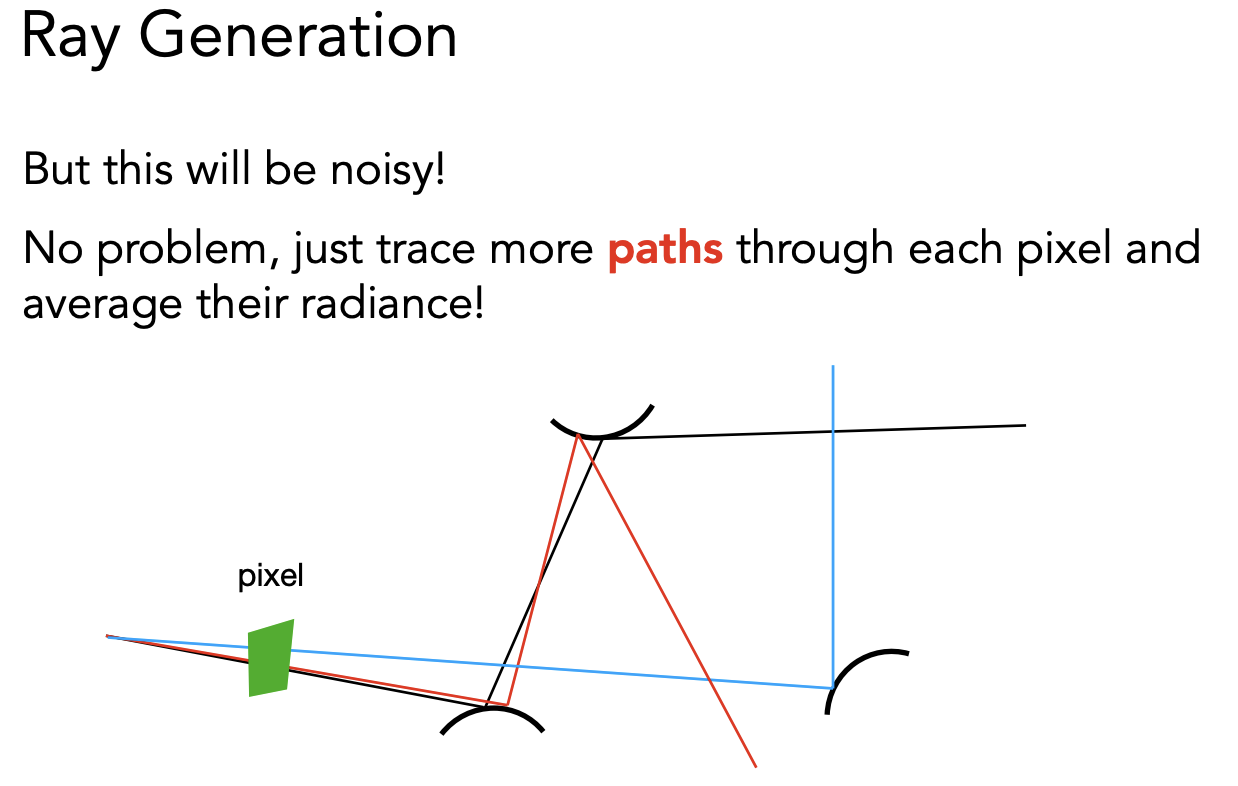
每个像素会有 n 条路径，把 n 条路径的着色结果加起来求平均：

​​​​

2.递归不会停下来

​​

如果限制弹射次数，又会有能量损失。

​​​​

于是引入了俄罗斯轮盘赌，以一定的概率决定是不是要停止追踪

​​

最终期望的结果就是正确的结果：

​​​​

现在可以得到正确的结果，但不够高效：

​​

光源小的情况下，很多 ray 会被浪费：

​​

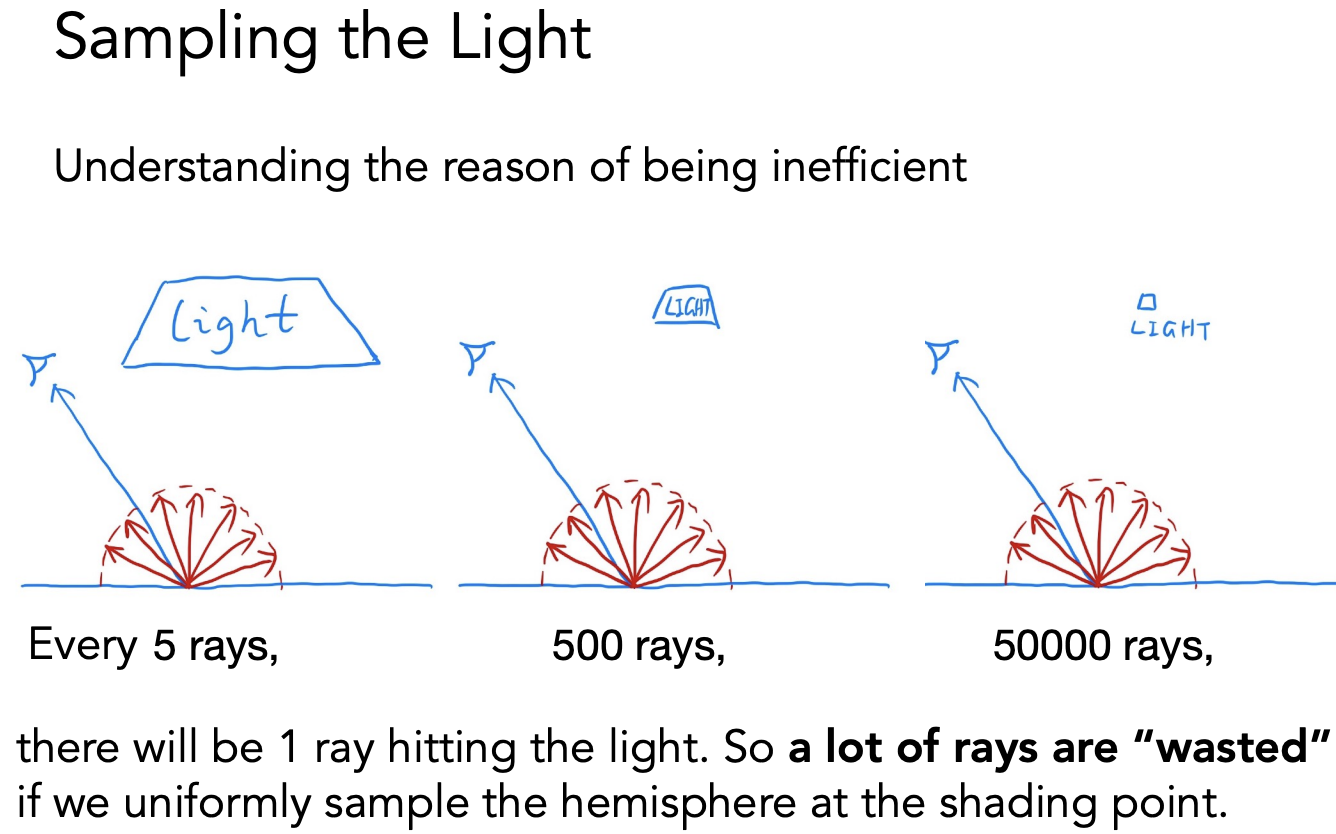
因此我们考虑对光源采样，从光源随机打出一条射线到着色点。

​​
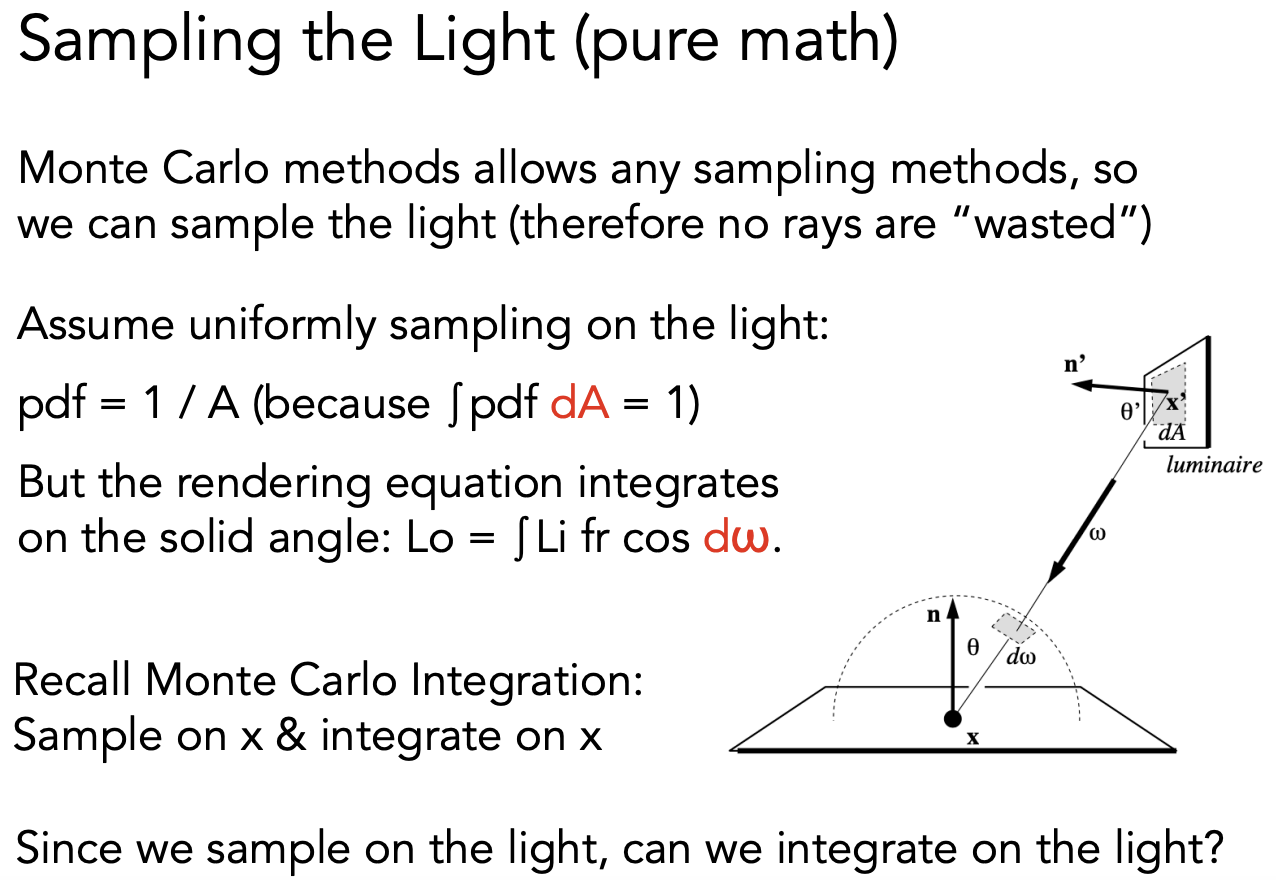
但前面提过蒙特卡洛在 x 上采样就得在 x 上积分，但是渲染方程是对立体角积分，但采样是在光源上采样。

因此，需要把渲染方程写成对光源积分的形式。

先找到 dA 和 dω 的关系：

​​

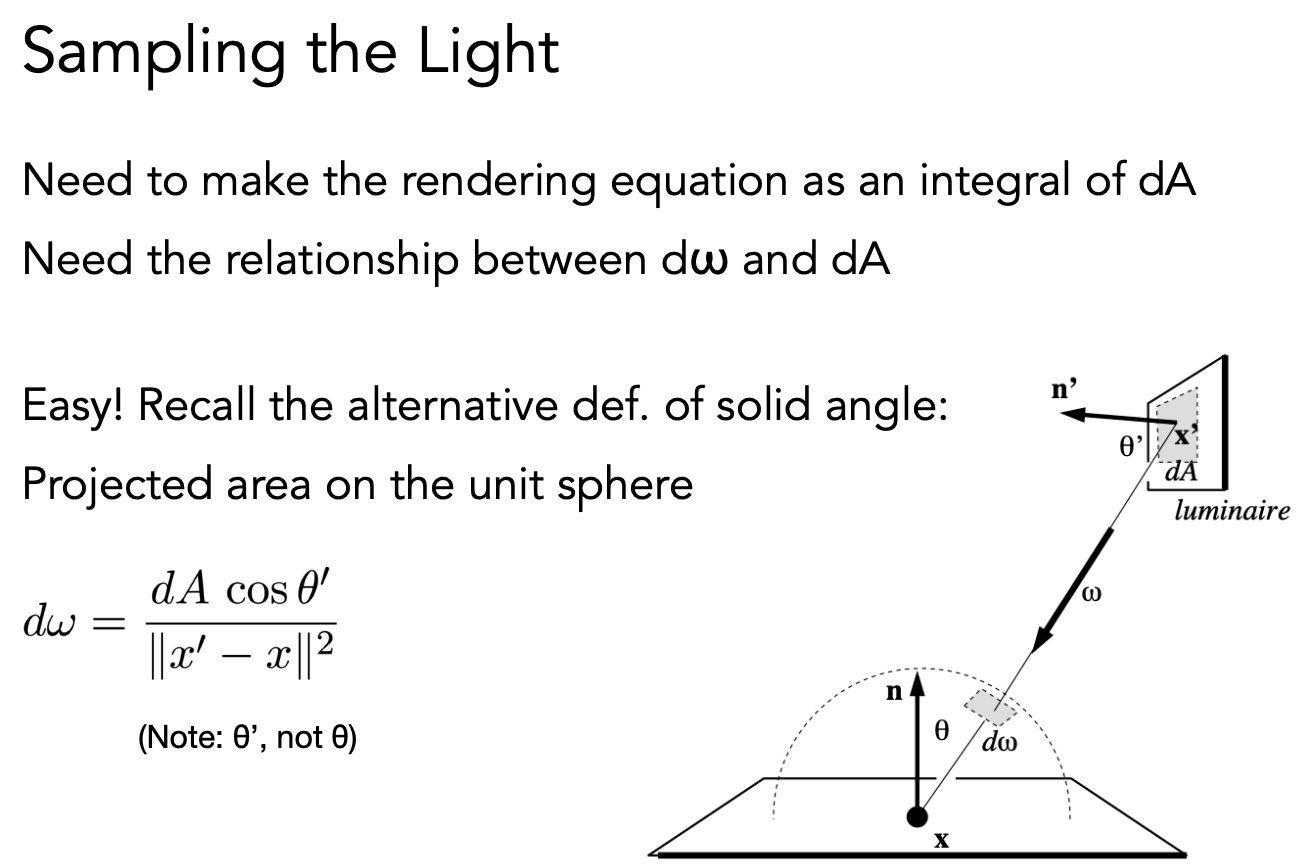
均匀地对光源采样：

​​

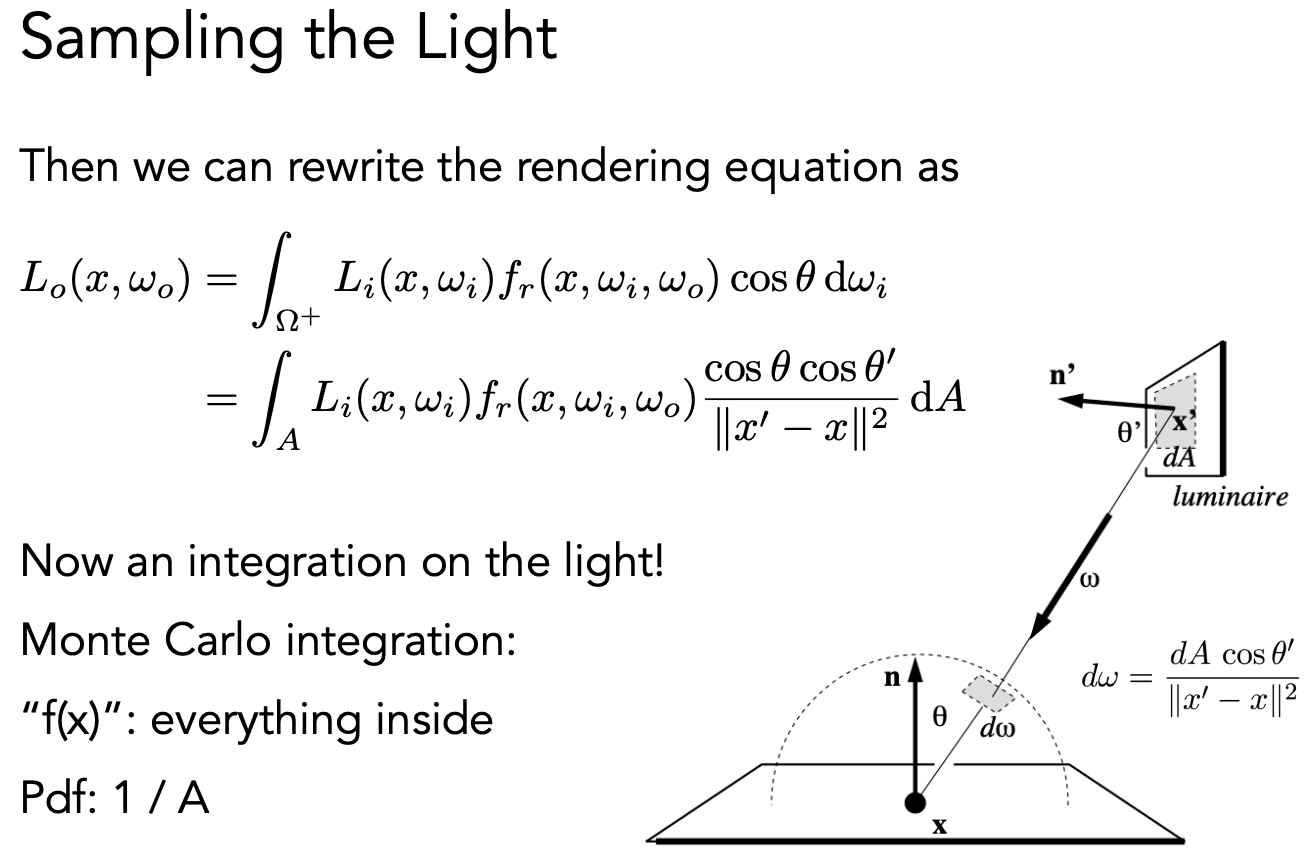
最后把这个光照分为两部分：光源直接照射的部分和其他反射的部分

​​​​

还有一个问题，需要计算光源被挡住的情况：

​​

比较过去和现代的 raytracing
过去特指 whitted-style ray tracing，现在是指光线传播问题的一些解决方法的大集合：

​​

还有一些没提到的问题：

怎么对半球均匀采样

怎么选择采样的 pdf（重要采样）

怎么生成真正均匀的随机数

能不能把光源采样和半球采样结合起来

把经过像素的每条光线的采样结果做平均时是怎么做平均，是否需要加权

算出来的 radiance 是怎么转换为颜色的

​​

​​​​