第十五章:Ray tracing 3 光线传播和全局光照
RayTracing 3 光线传播和全局光照
回顾上节课
基础的光线追踪
- 光线生成
- 光线和对象求交
加速
- 光线和 AABB 盒求交
- 空间划分 VS 物体划分
- BVH 遍历
辐射度量学
本节课
继续辐射度量学
光线传播
- 反射方程
- 渲染方程
全局光照
概率论
回顾上节课的概念
Radiant energy Q
Radiant flux(power)(单位时间的能量)
Radiant intensity (单位立体角的能量)
Solid Angle(立体角)
我们考虑光照都是用瞬时量,因为物体一般接受能量一边也在辐射能量,有一些荧光的材质可能收到光线时间长短影响有不同的颜色,这种情况先不考虑。
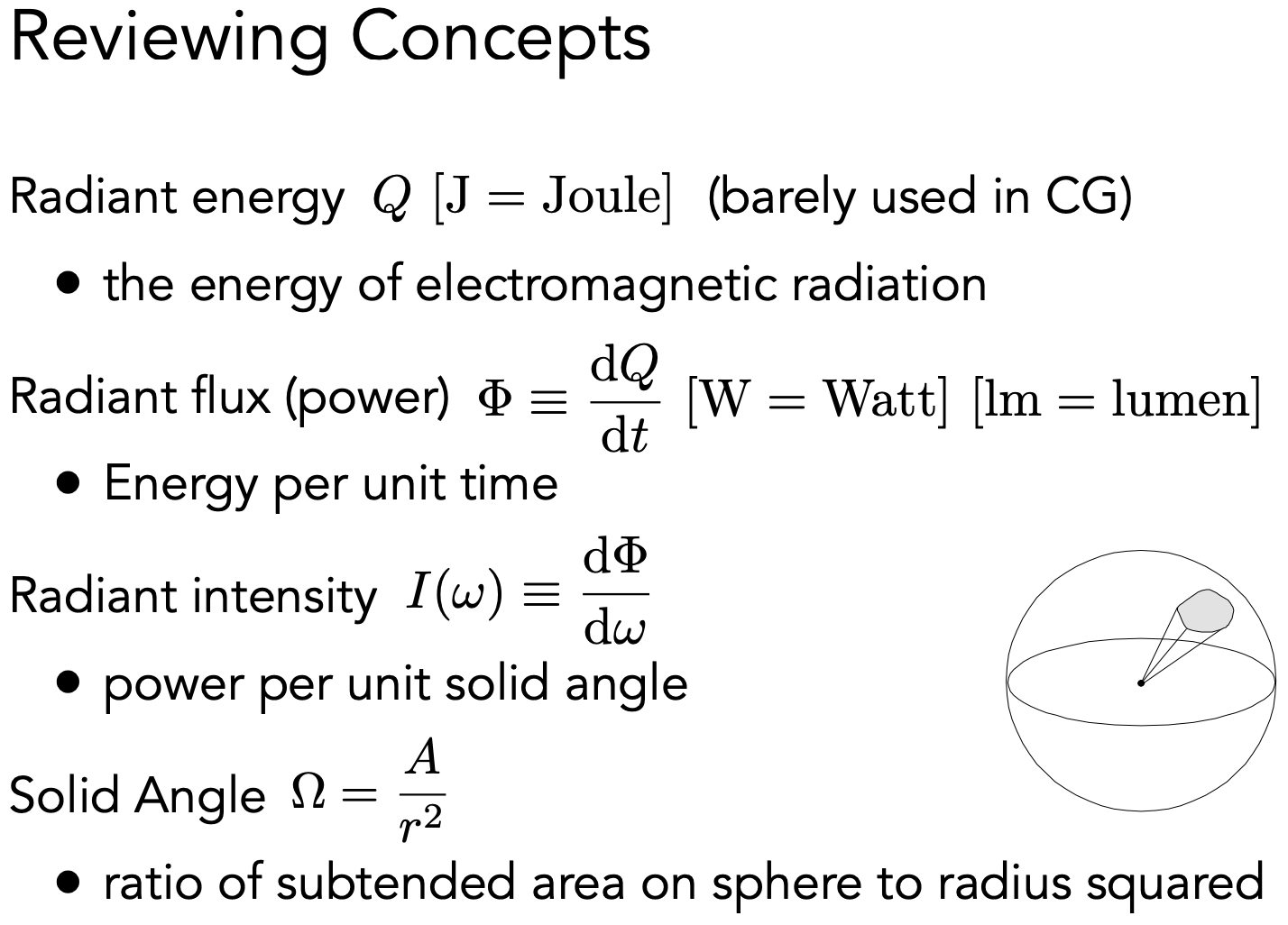
微分立体角
(θ,Φ)不是均匀的划分球体面积,靠近顶(底)部,sinθ 小,微分立体角小,靠近球中间,sinθ 大。
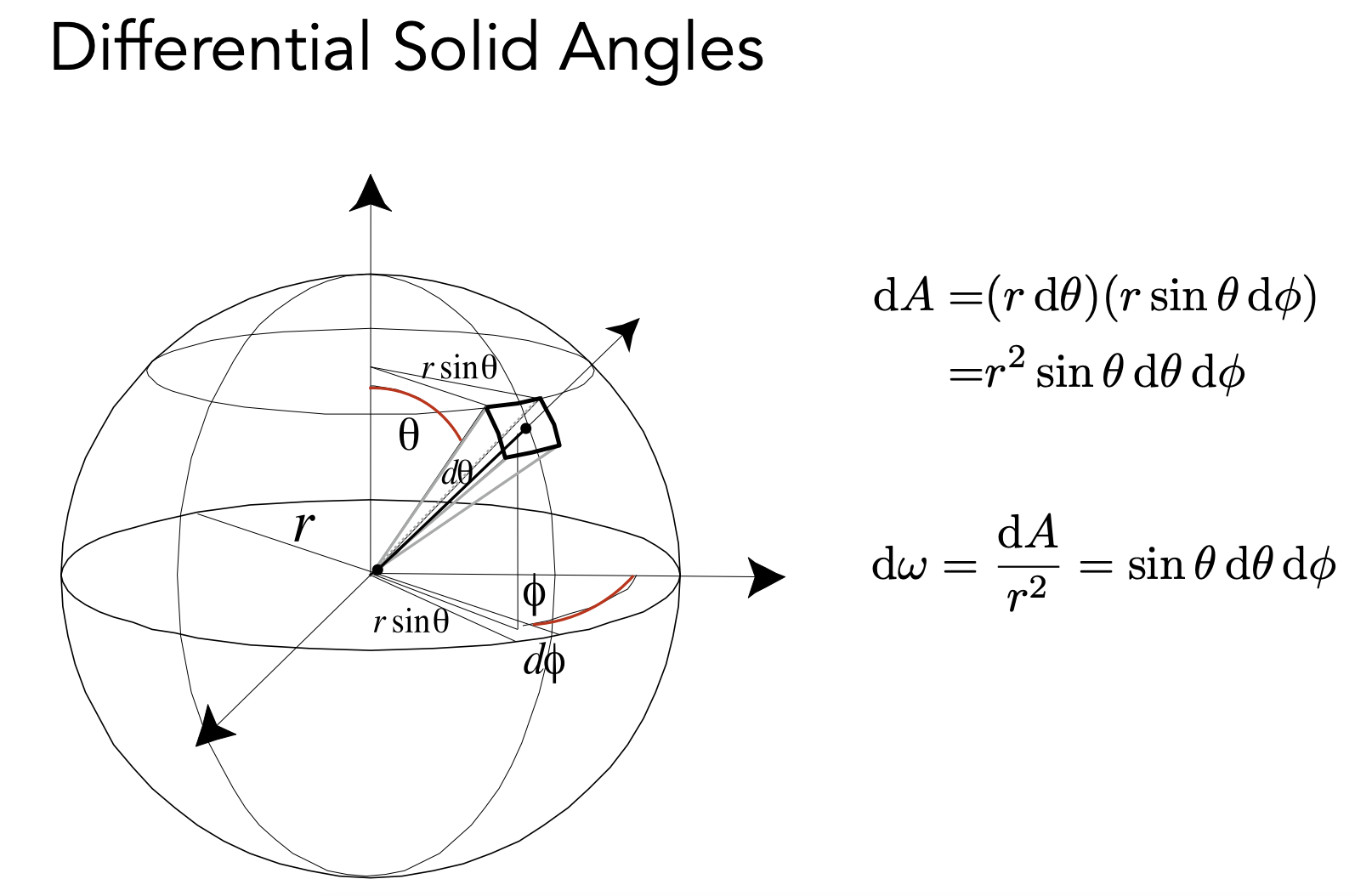
Irradiance(power per unit area)
单位面积垂直方向上的光线的能量,光如果不是垂直的,需要计算垂直方向的投影
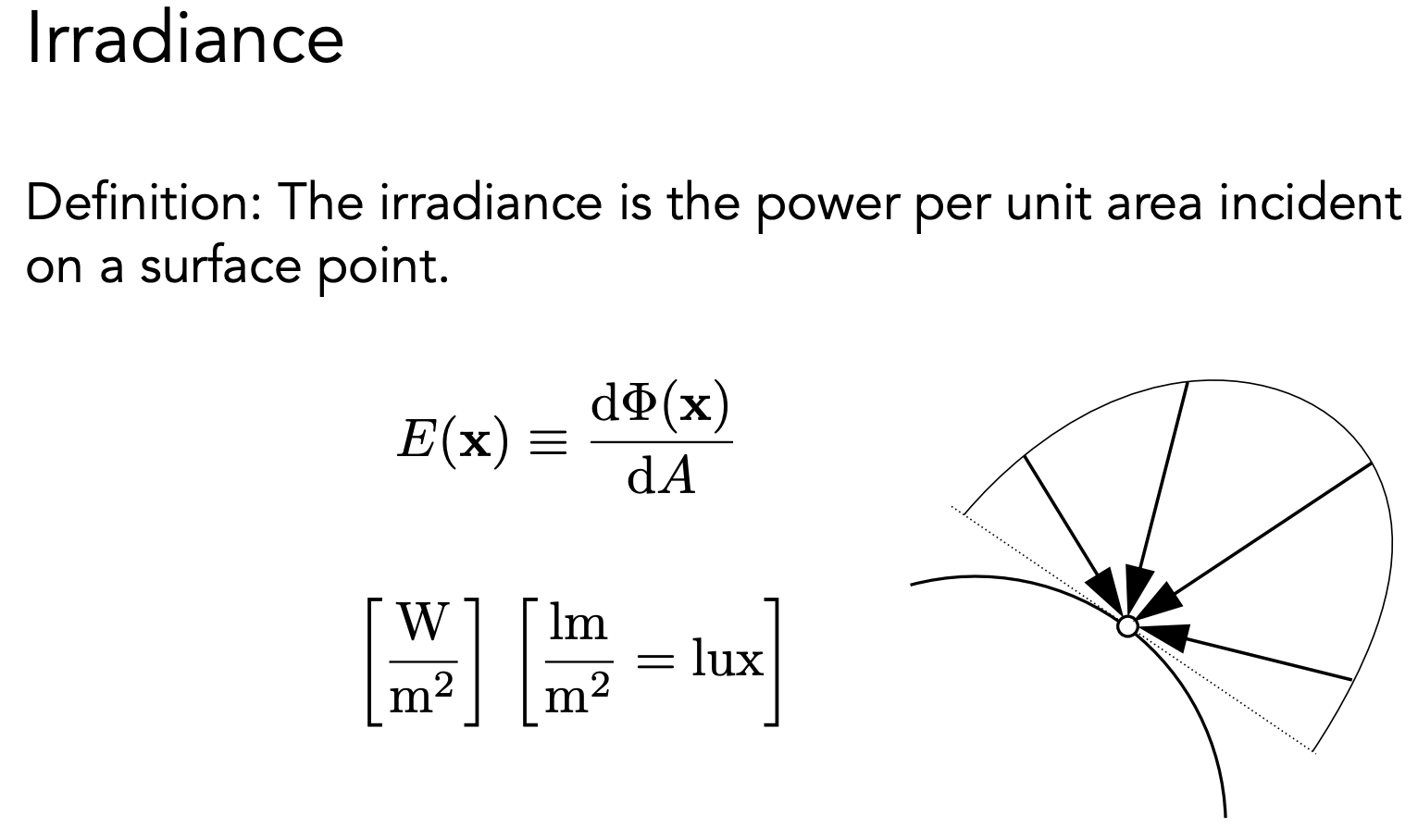
夏天太阳垂直照射,冬天有一个倾斜角度
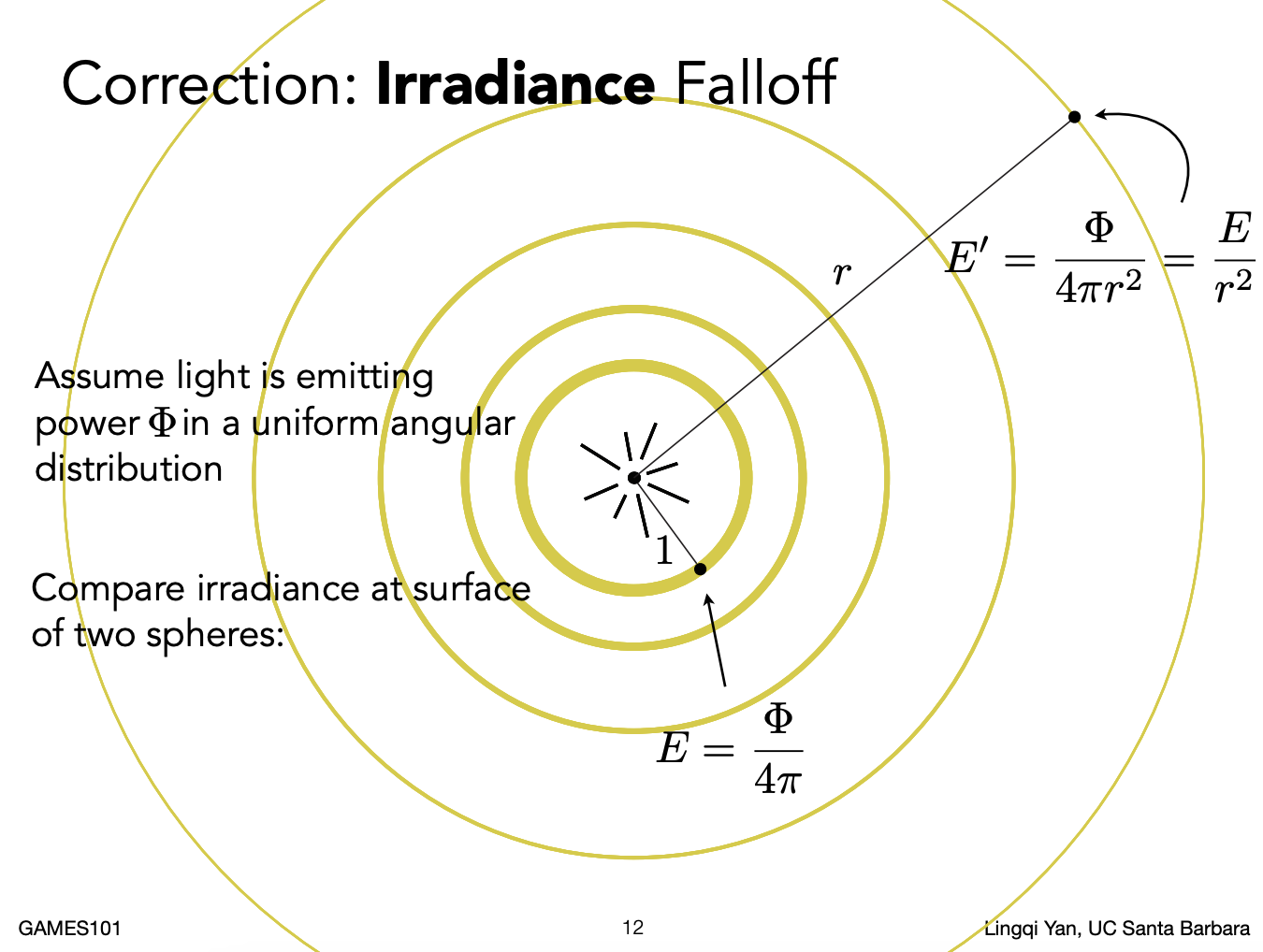
Irradiance Fallof
单位立体角的能量不会衰减(r 越大辐射面积越大,单位体积角始终不变),单位面积能量会衰减。
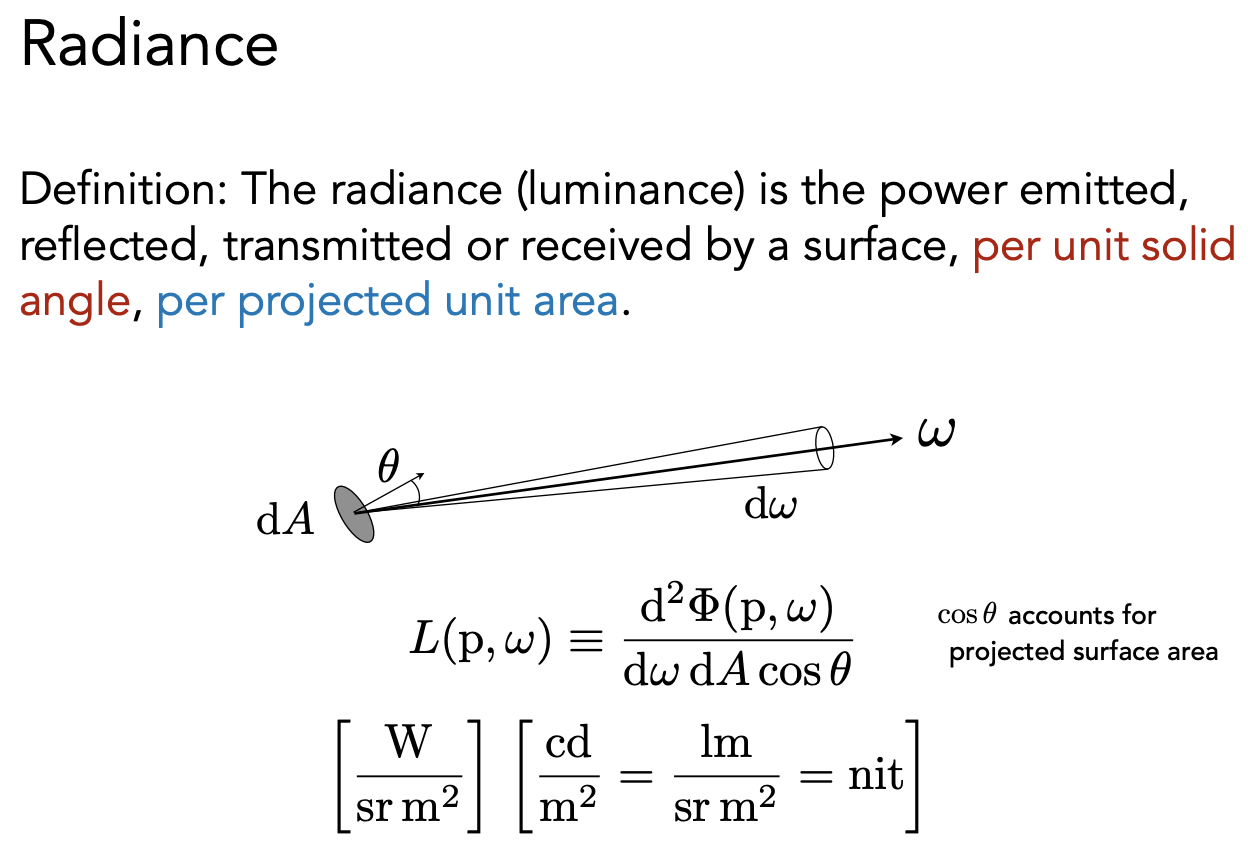
Radiance
光线传播过程中带的能量。单位立体角、单位投影面积上的能量。

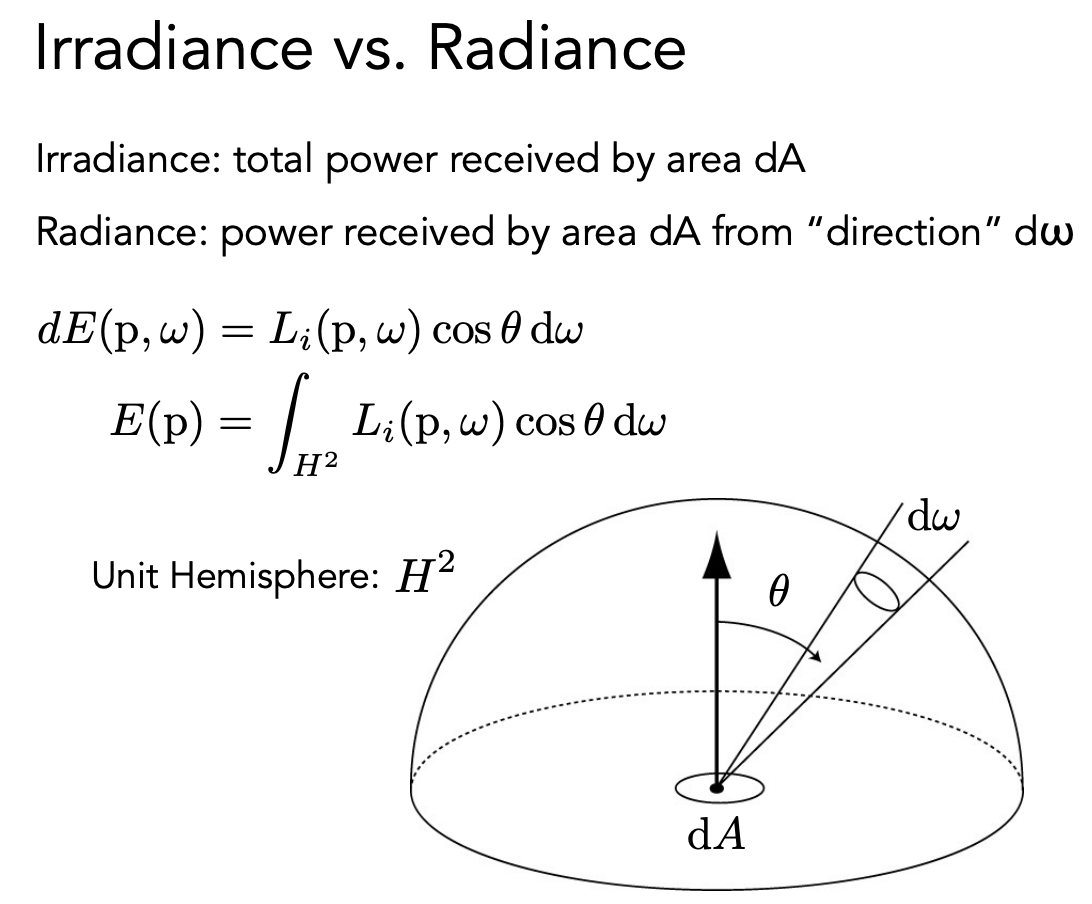
irradiance 和 radiance 的区别:是否有方向性。radiance 可以理解为单位面积上某个方向接受到的能量。

也可以用 intensity 来理解,即一个单位面积上往一个方向辐射出去的能量。

对各个方向的 radiance 积分得到 irradiance。H 平方表示半球。
反射方程:
Bidirectional Reflectance Distribution Function (BRDF, 双向反射分布函数)
理解反射:
可以理解为光线发射到一个物体表面,被吸收了,再从某一个角度发出去
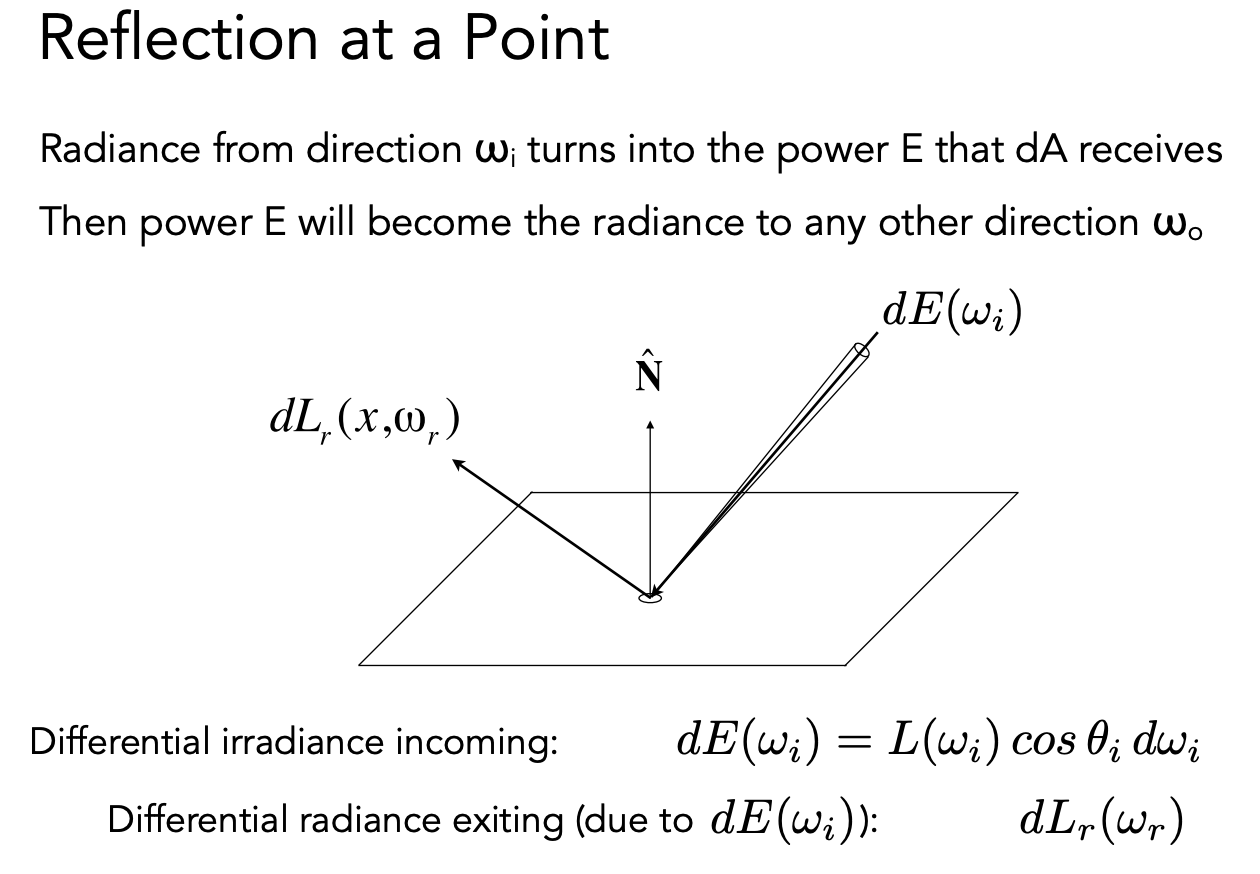
dE(ω_(i))表示 dA 在一个方向上的单位立体角接收到的能量,dL_(r)(ω_(i))表示一个比率:dA 上任何一个出射方向算出来的 radiance 除以 dA 接收到的 irradiance。
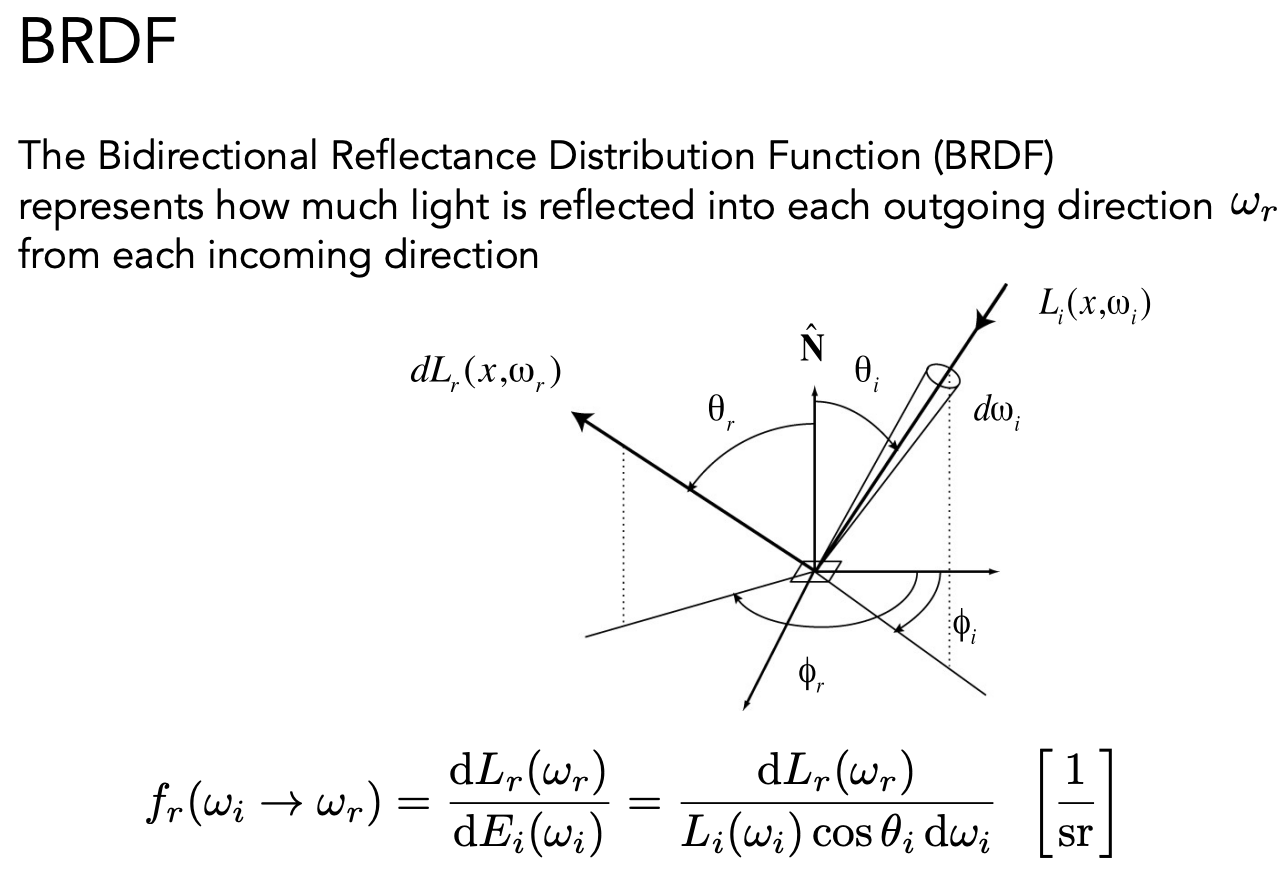
BRDF 定义了光线和物体是怎么作用的,定义了不同的材质
任何一个输入方向对观测方向的贡献加起来得到最终的光照
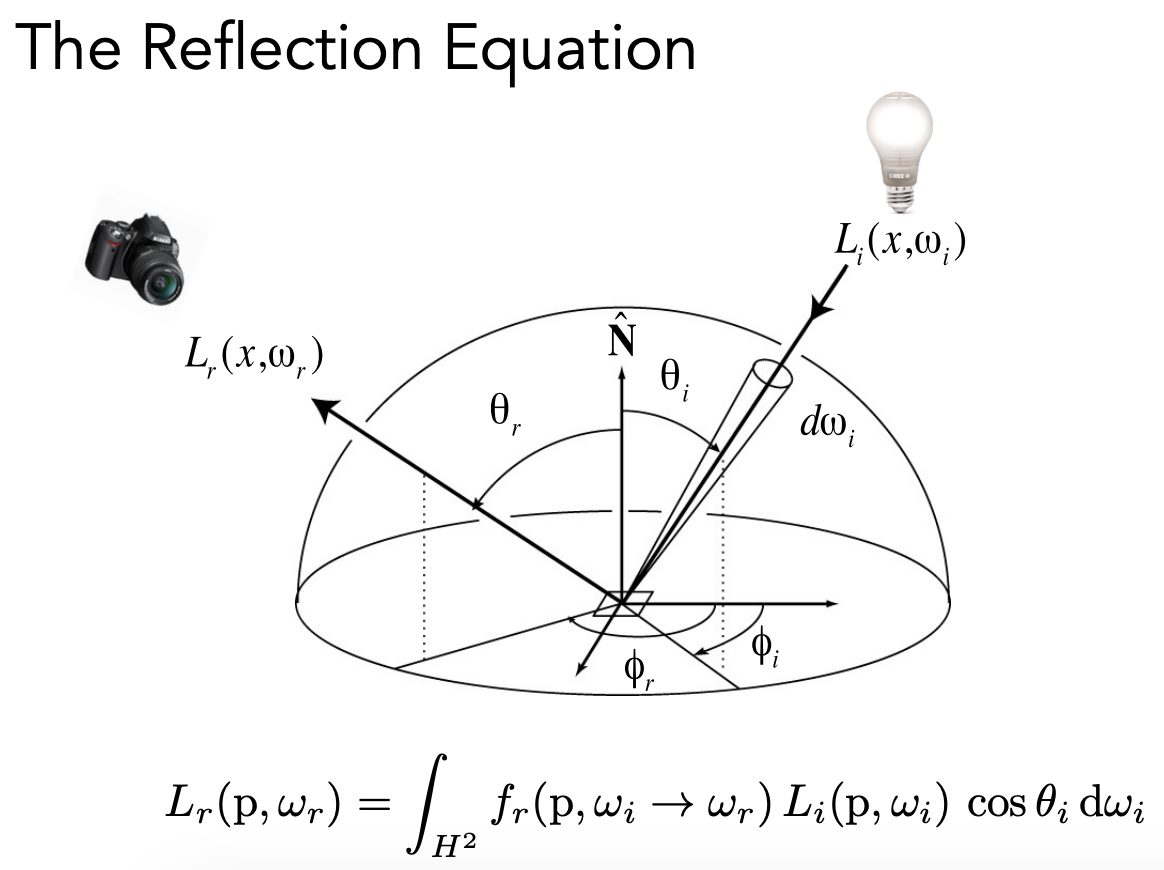
光线会弹射多次,任何出射的 radiance 都有可能成为入射的 radiance,所以是一个递归的问题。

渲染方程(绘制方程)
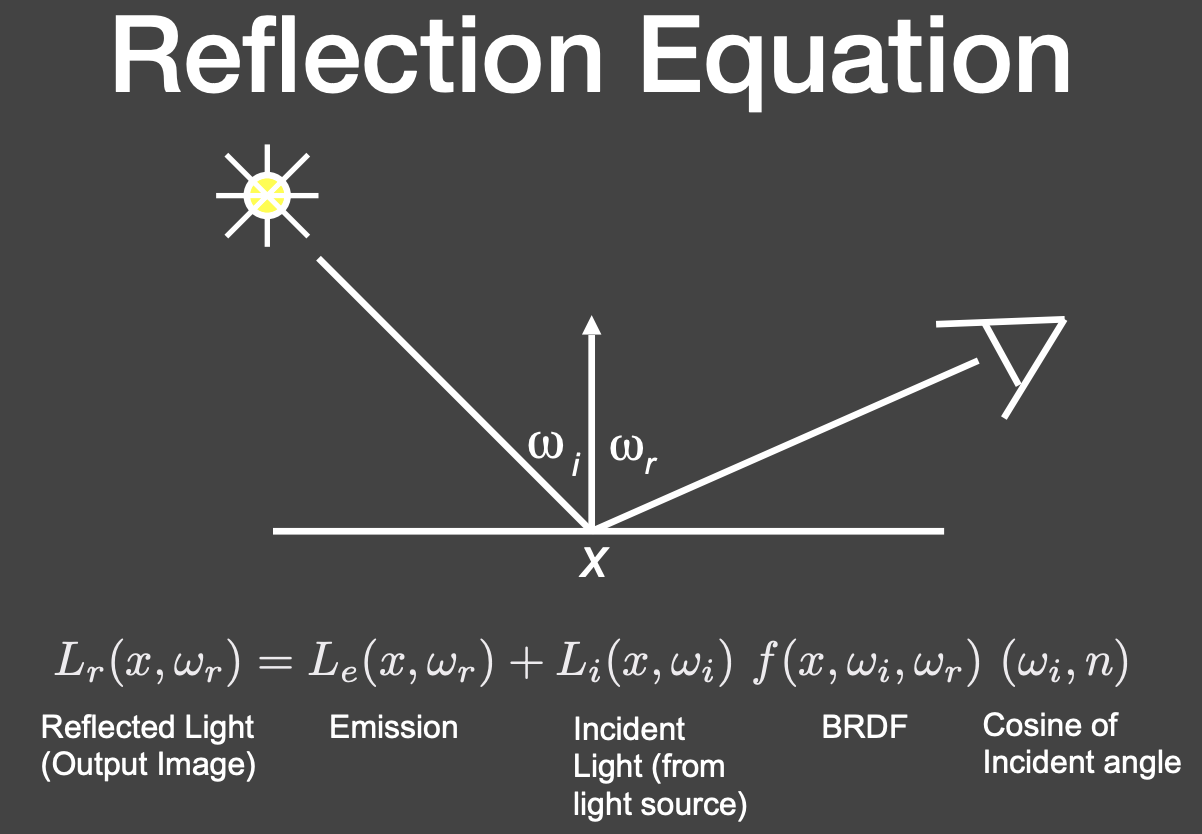
假如物体自己会发光,出射的光线包含两部分。

方程中假设所有方向都是向外的。
一个点光源:
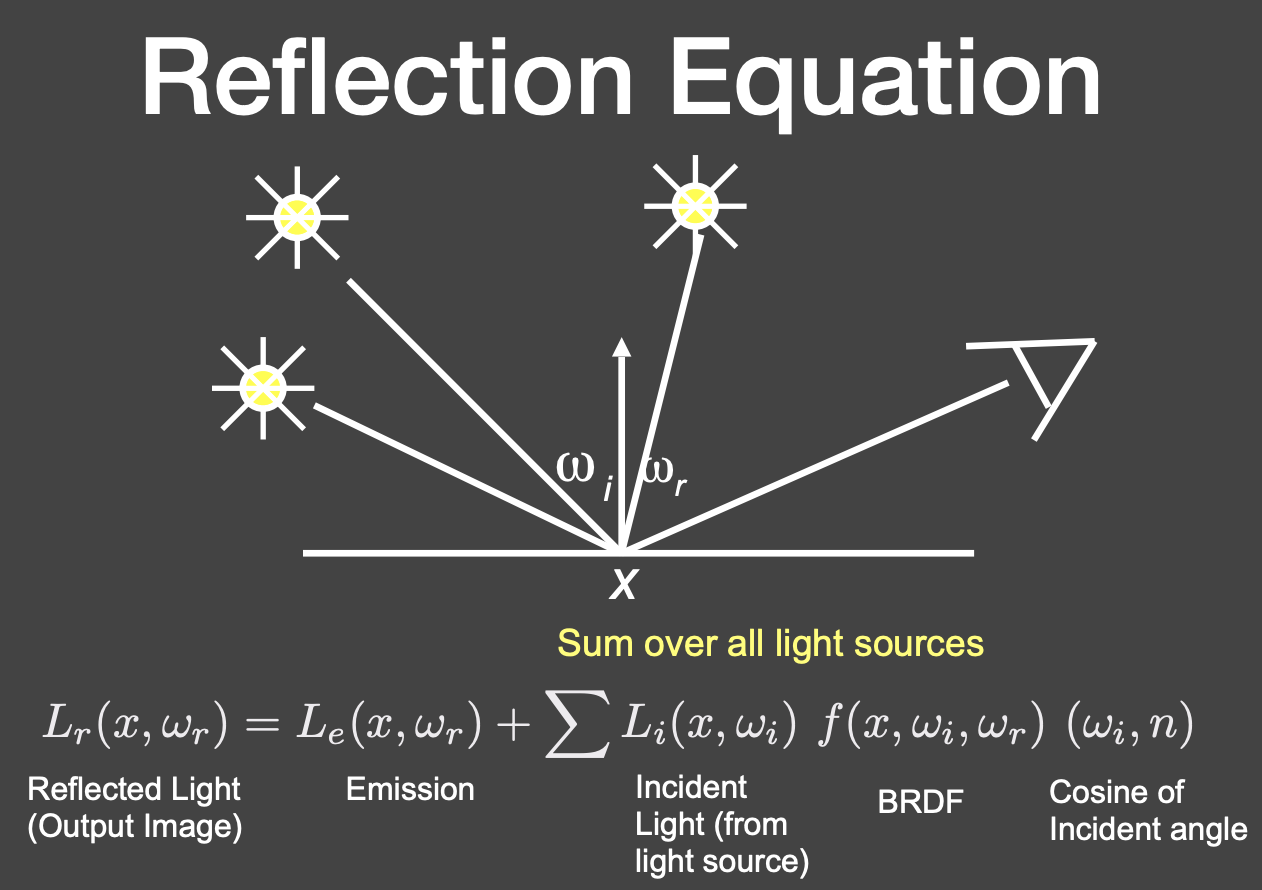
如果有很多点光源,就把每个点光源的反射加起来:
如果是一个面光源,就把面光源上每个点的反射积分:
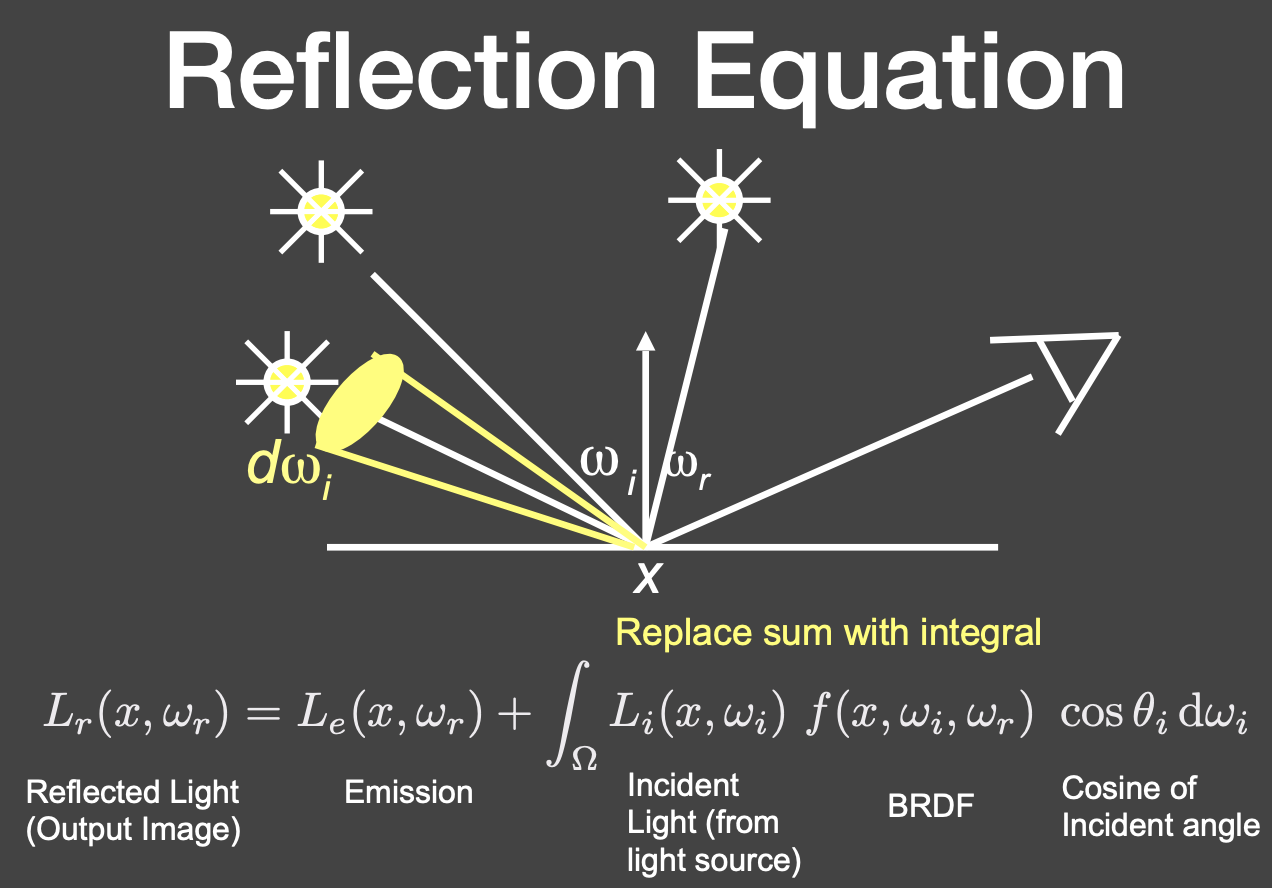
radiance 不只是从光源发出的,也有可能是其他点反射的 radiance。
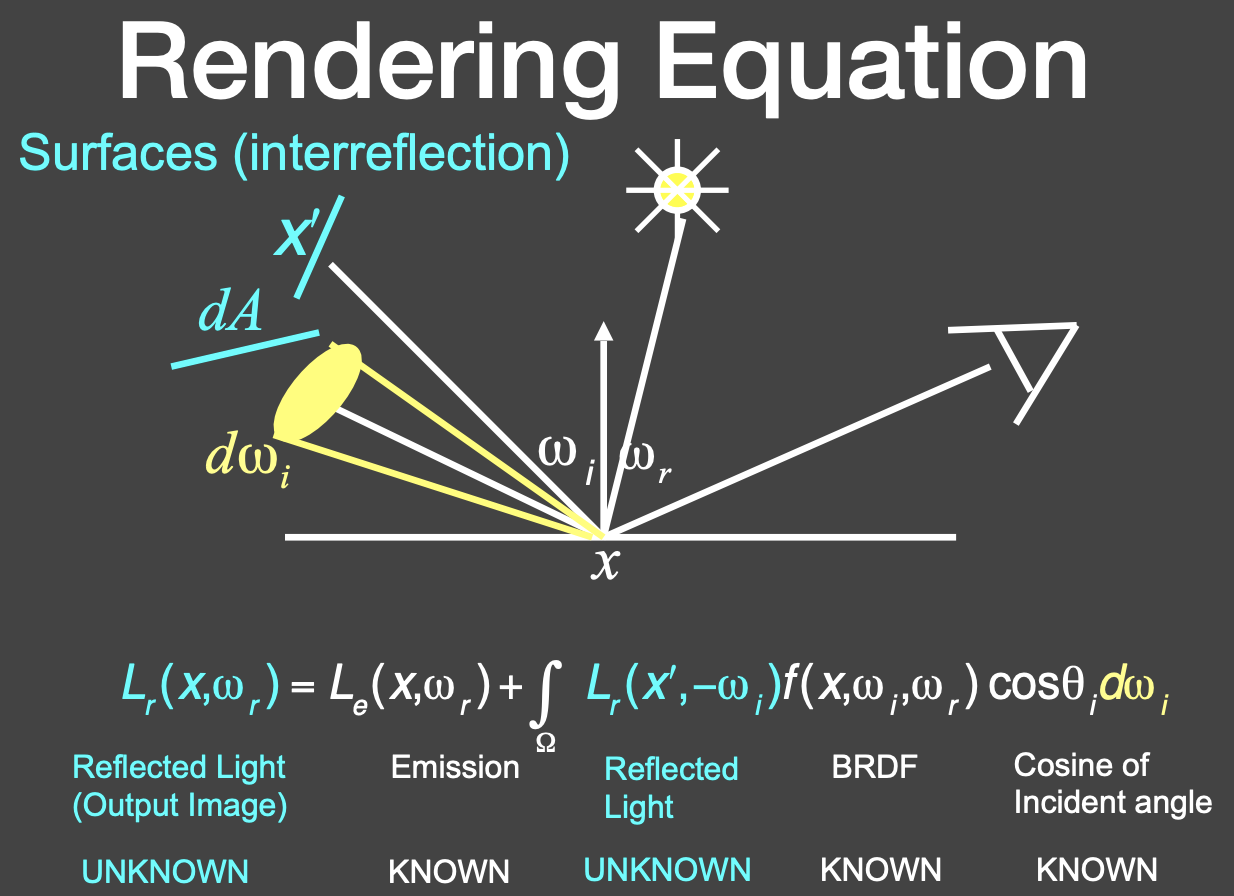
简写渲染方程:

写成算子的形式:
E:光源发出的能量,K:反射操作符,KL:反射的能量

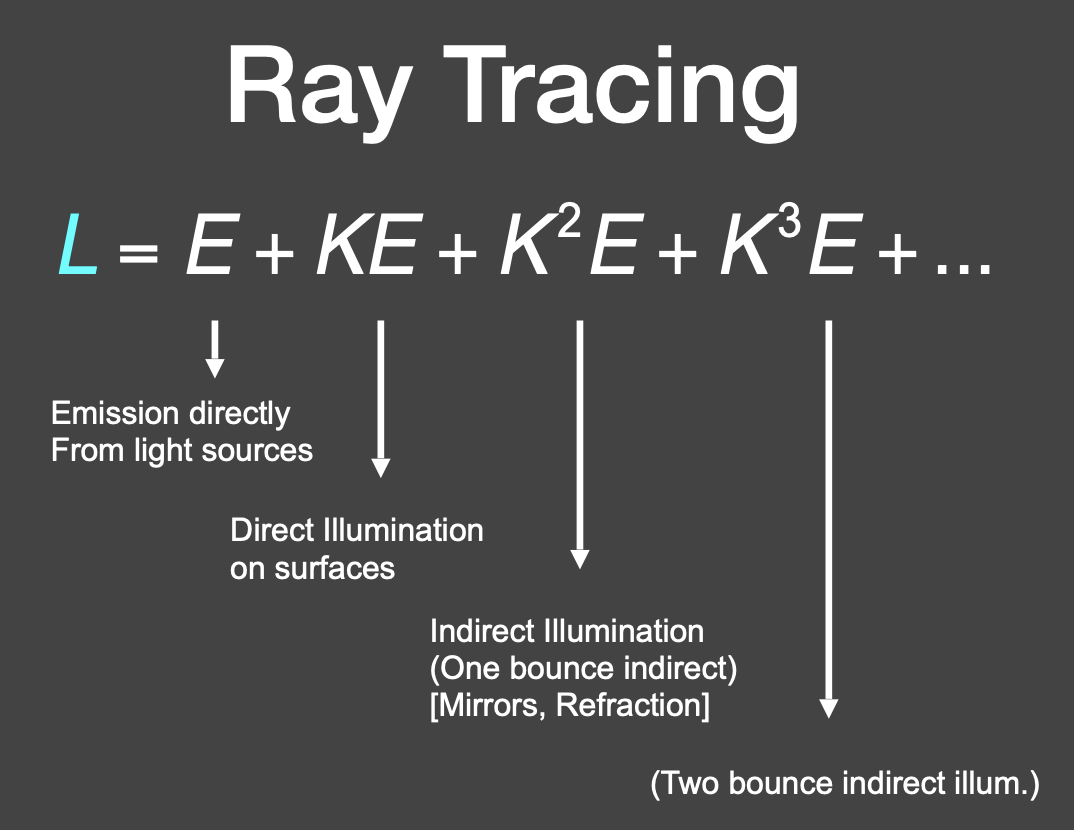
求解 L,下图 I 表示单位矩阵,最后 L 可以写成一种泰勒展开的形式:

L 表示为一种弹射次数的分解:
弹射 0 次:光源自己
弹射一次:直接光照
弹射两次及以上:间接光照
全局光照:直接和间接光照的集合
光栅化做的部分:弹射 0 次和 1 次,后面的部分光栅化很难处理,因此用光线追踪来处理
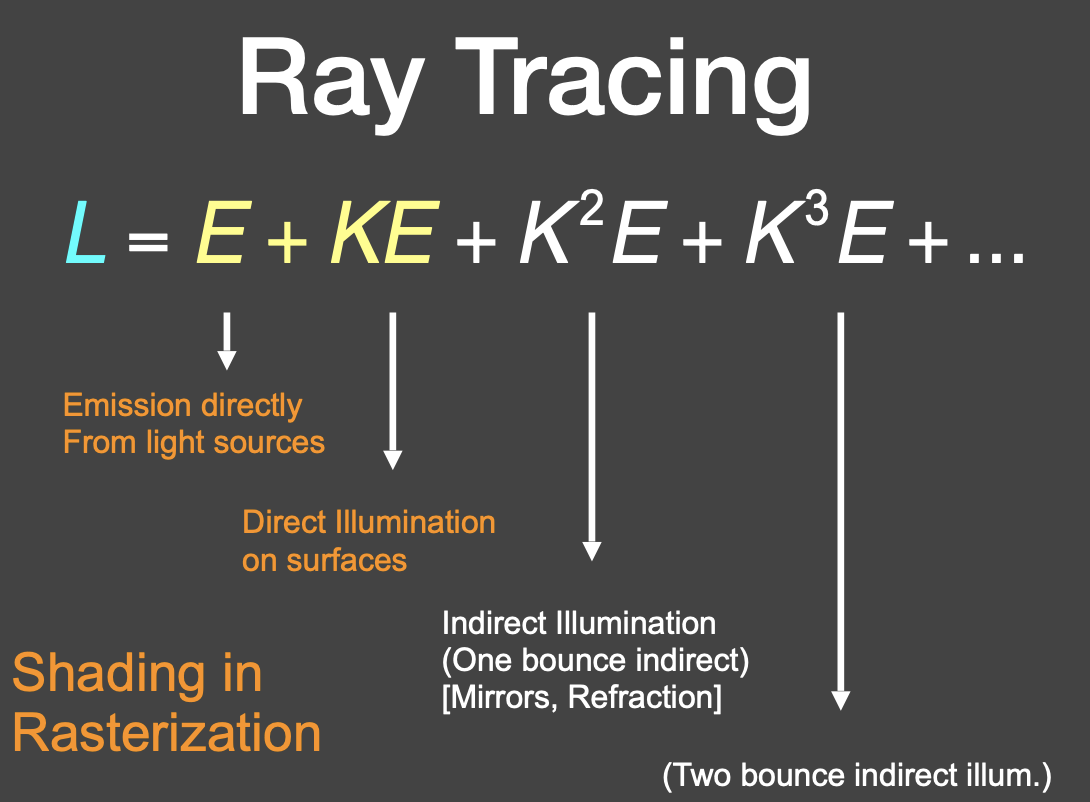
接下来求解渲染方程。
需要一些前置的概率论知识:
X:随机变量
p(x):随机变量的概率分布

概率:

期望(平均):

连续情况下描述变量和分布(概率密度函数):

如果有一个随机变量的函数,函数的期望等于函数在某个变量的值乘以对应的概率密度再积分。