第十三章:Ray tracing 1 基础光线追踪算法
Ray Tracing(光线追踪)
光栅化的问题
不能很好地处理全局效果,比如:
1.软阴影
2.光线多次弹射(毛玻璃反射、间接反射)

光栅化速度快,但是质量低;光线追踪准确但是速度慢。所以一般光栅化用于实时、光线追踪用于离线。

基础的光线追踪算法
光线的三种假设:
光沿直线传播(实际并不是
光线相交时不会碰撞(实际并不是
光线从光源传播到眼睛(根据光的可逆性,光线以不变的光路从眼睛传播到光源
![image]()
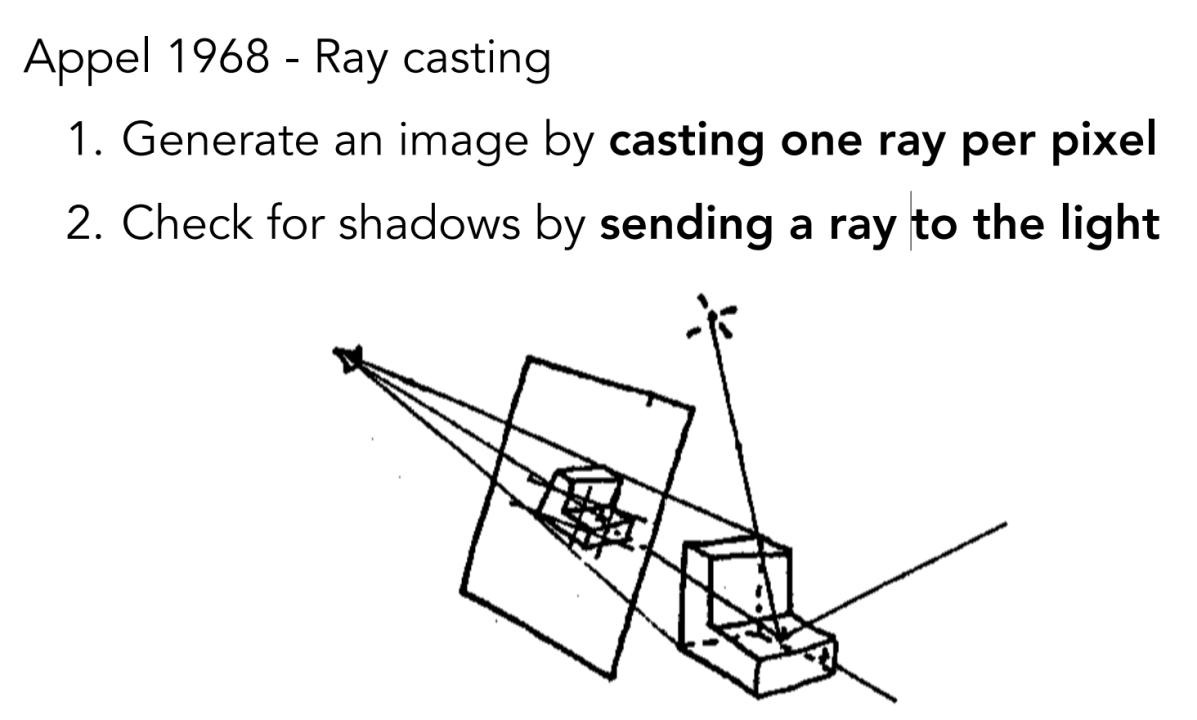
光线投射
从摄像机到成像平面中的一个像素连成一条射线,这个射线会和一个物体相交。再把这个交点和光源做连线,判定他是不是在阴影内。
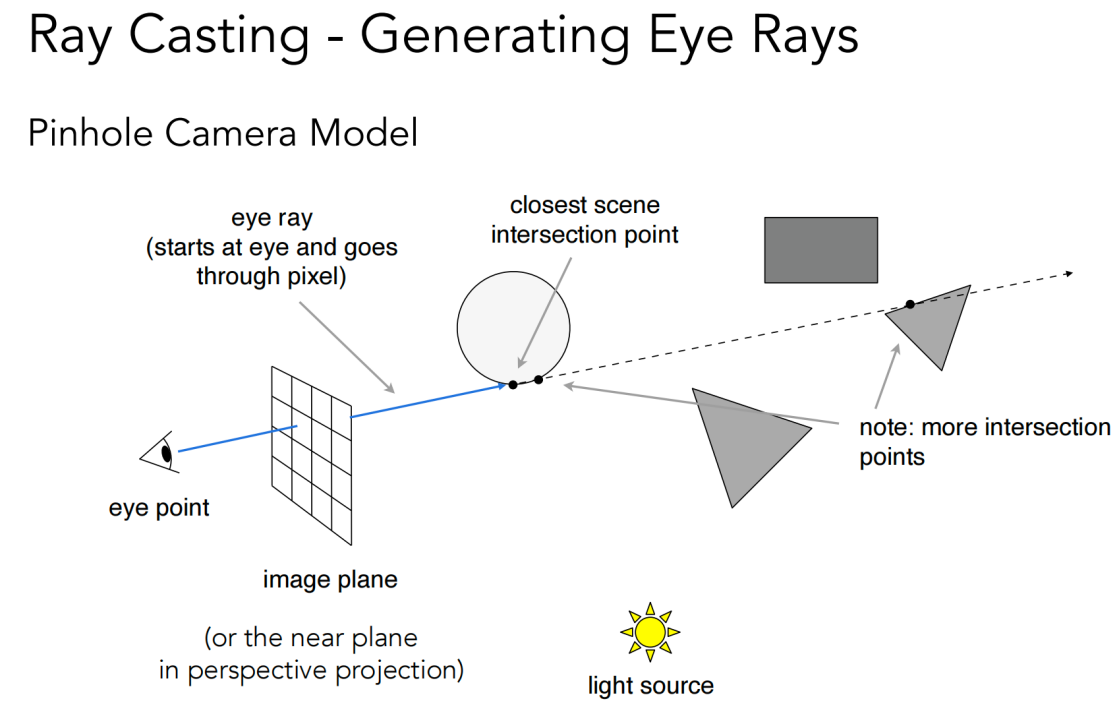
假设眼睛是一个点(针孔摄像机),同时光源也是点光源。光线打到场景中的物体会发生完美的折射和反射。
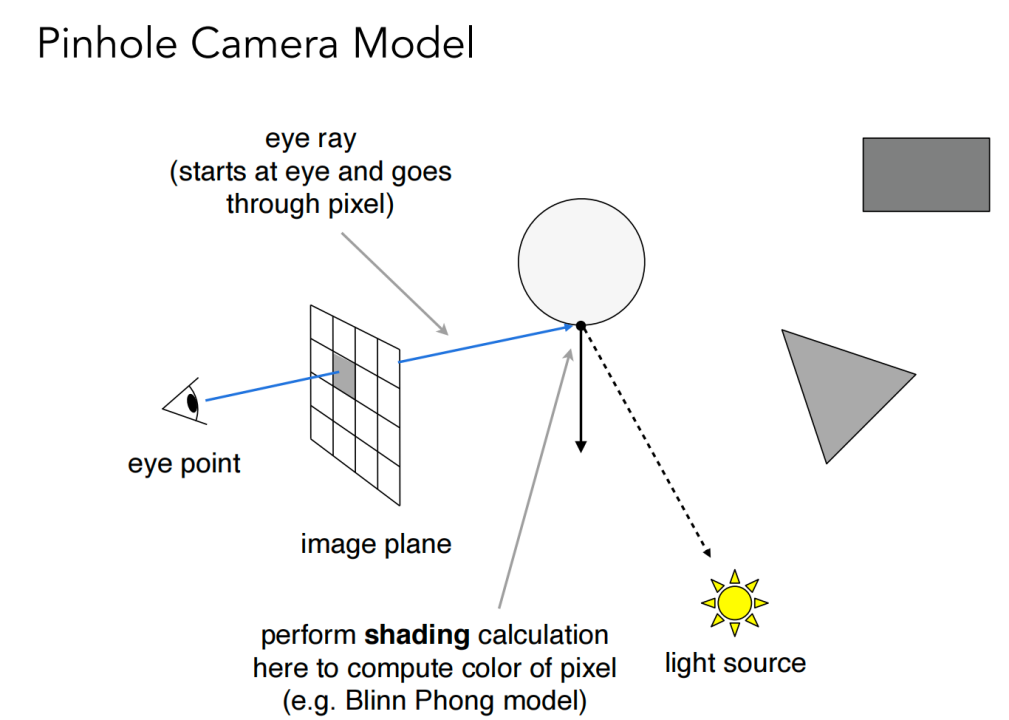
考虑光线和场景中的物体最近的交点,交点再与光源做连线,如果没有遮挡说明没有阴影。求出交点后再对交点做着色。
recursive Whitted-styled ray tracing
光线可以不断弹射。每个弹射点可画出一条 shadow ray,计算是不是在阴影里,光源弹射后能照到的点的着色值最后都加到一个像素里面去。
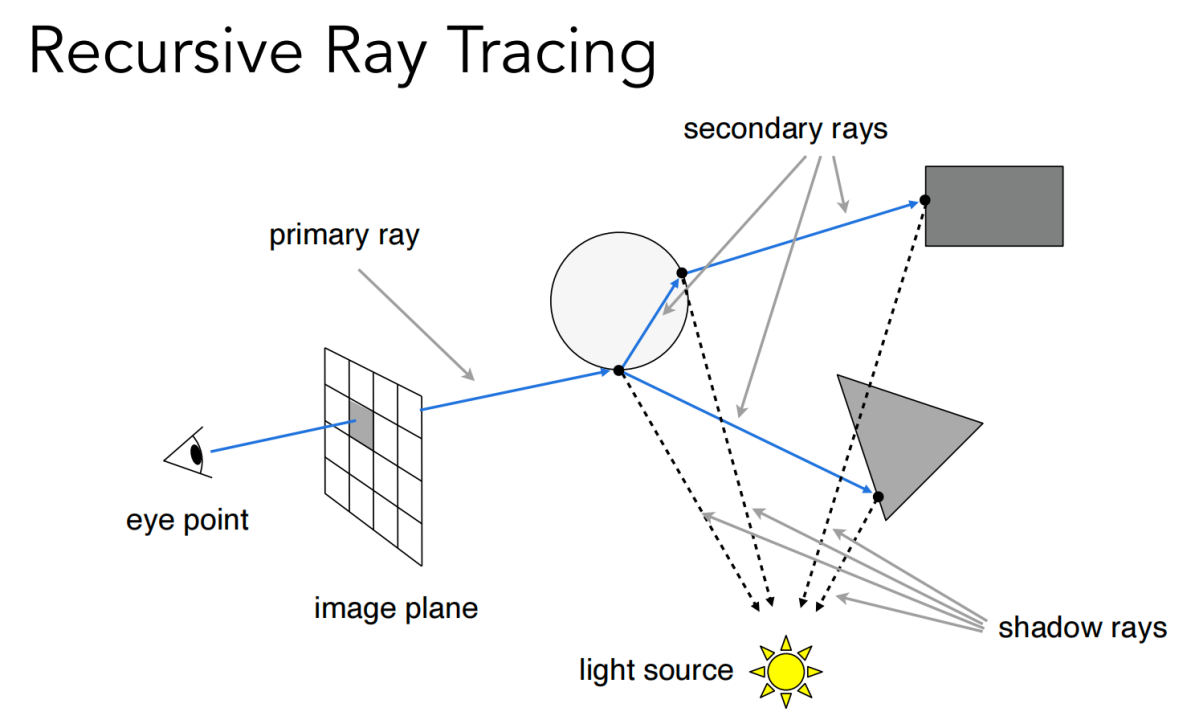
求光线和物体表面的交点
光线的定义:
点光源:起点 + 方向

判断光线与球体是否相交:
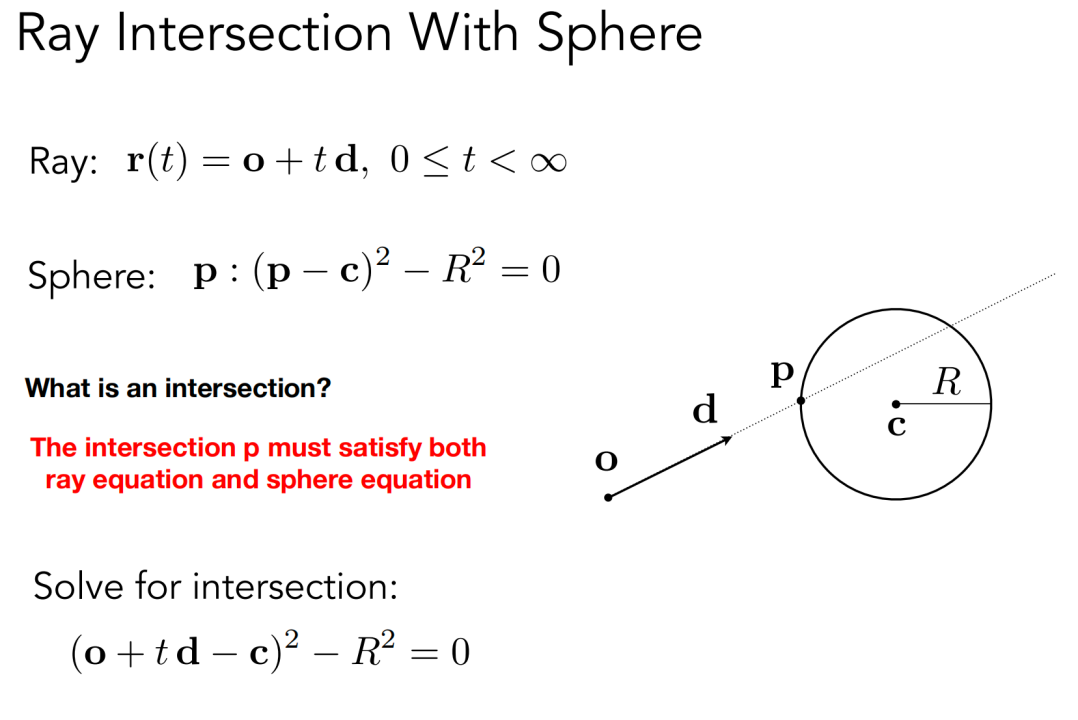
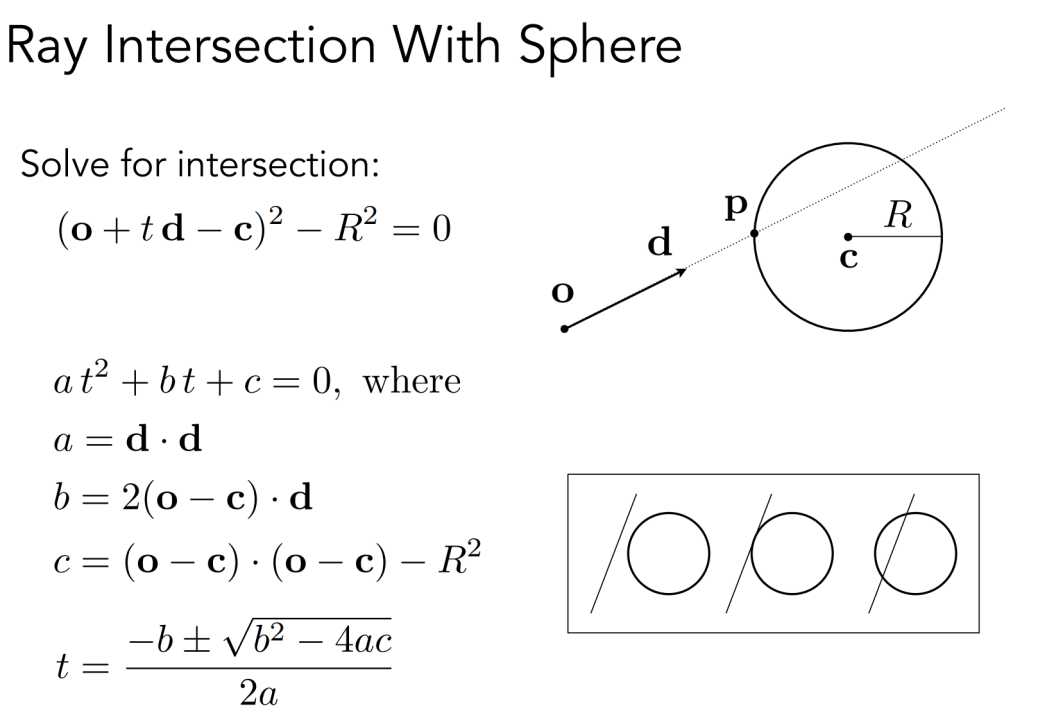
点即在光线上,又在球上。求解一元二次方程:
对于一般面
隐式表示:列出 surface 的隐式表达式,带入求解:

显式表示:求光线与三角面的交点
一个封闭的图形,从图形内部发出一条射线,与图形的边的交点数量一定是奇数

简单做法:一个一个三角形求解是否与射线相交
先光线与平面求交,再判断一个点是不是在三角形内部
用一个法线和一个平面上的点可以确定一个平面
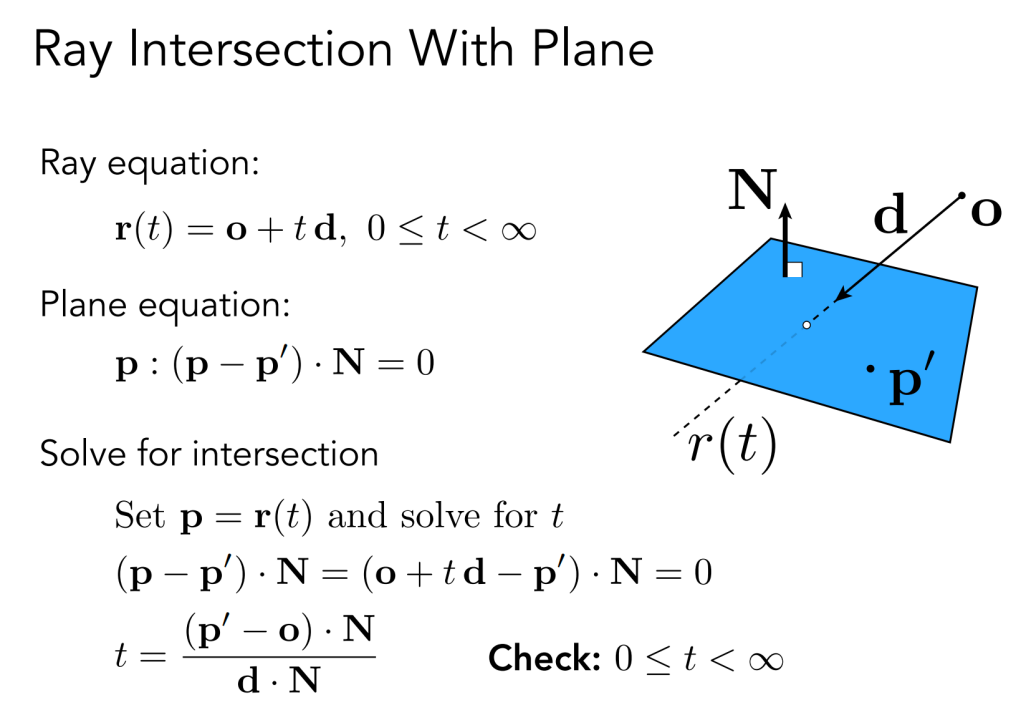
Möller Trumbore Algorithm
快速求交点(重心坐标表示平面上的点)
解线性方程组
b1 和 b2 必须是非负的

加速光线和表面求交
如果每个三角形都求一次交点很花时间

用包围盒进行加速
如果一个光线碰不到包围盒,那就不可能碰到包围和里的物体

三个对面形成的交集
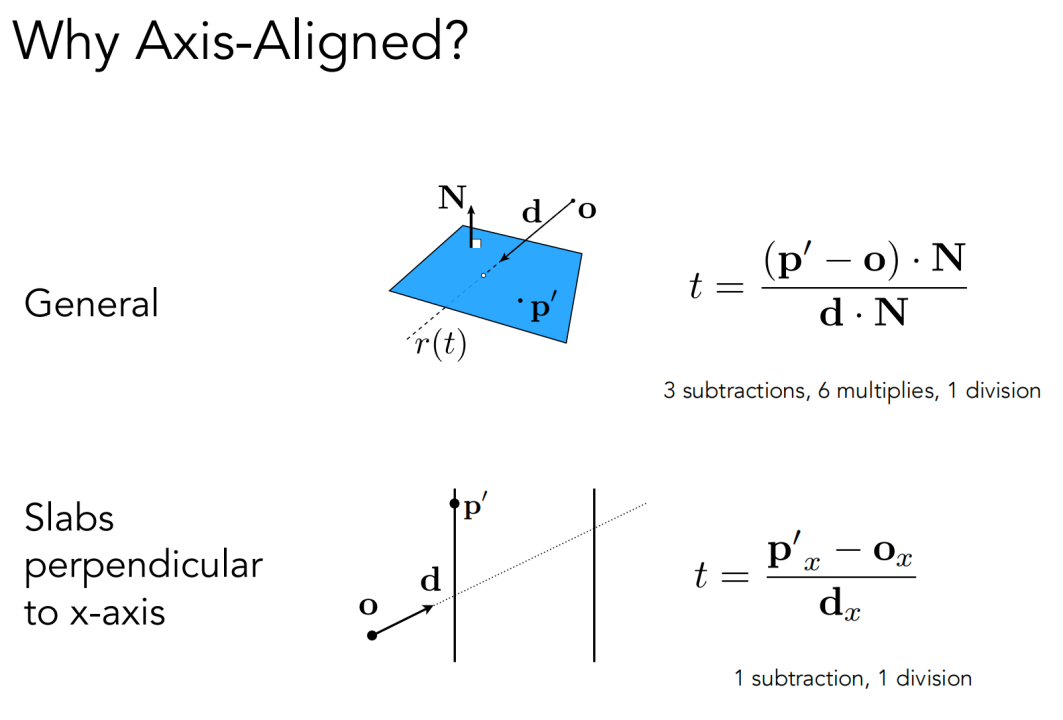
通常用 AABB 包围盒(和坐标轴平行的包围盒)
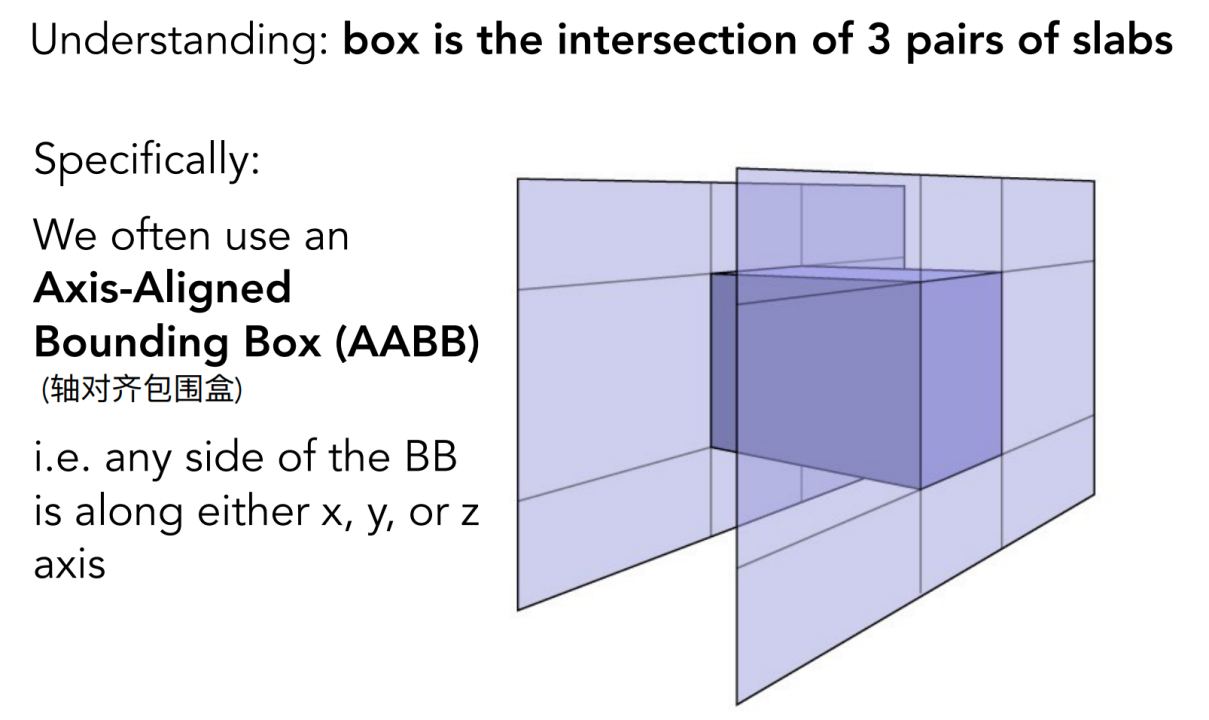
2D 求交:
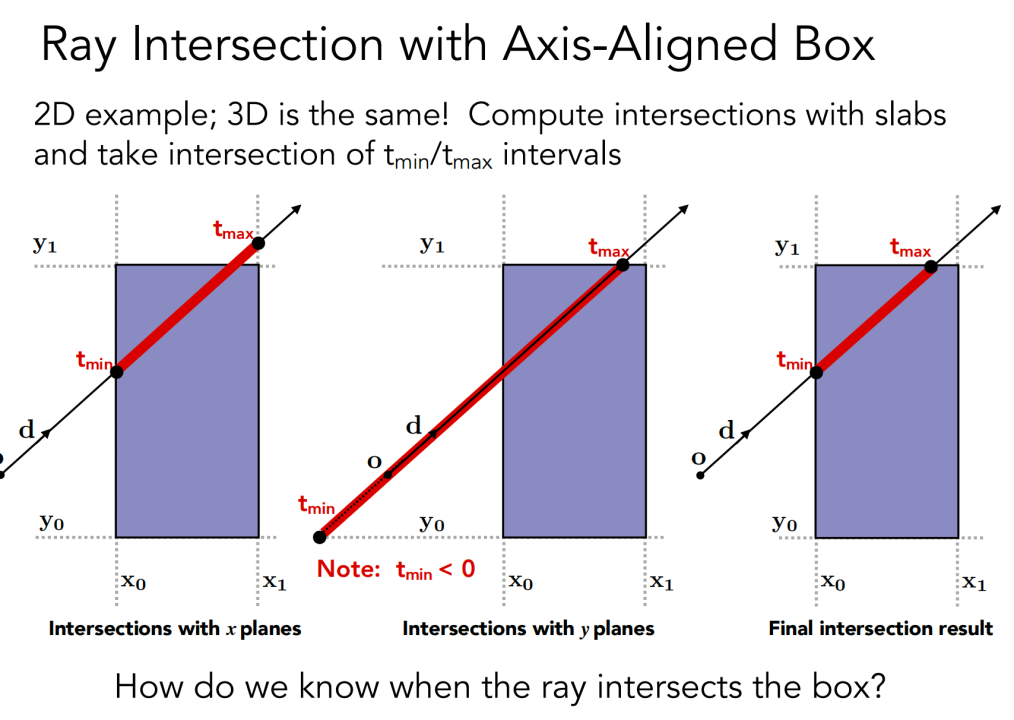
3D 求交:
3D 下有三组对面,光线要进入所有面才算进入盒子,只要出了一个面就认为出了盒子
3D 对三组对面分别计算进入的最大时间和出来的最小时间
如果出来时间小于进入时间,说明光线在盒子里待了一段时间

离开时间小于 0,说明盒子在光线背后
如果进入时间小于 0,说明起点在盒子里

用 AABB 包围盒更好计算