第十一章：显示几何，曲线、曲面

几何入门：

• 几何例子

• 不同表示几何的方式

  • 隐式
  • 显式

本节课：

• 显式几何

• 曲线

• 曲面

显式几何有不同的表示方法：
三角形面、贝塞尔曲面、点云

点云

物体用一堆点表示。

只要点足够密，可以表示任何形状的几何。

点云转换三角形面。

多边形面

三角形、四边形面。

需要用更复杂的数据结构表示三角形对连接关系。

是图形学中最常见的表示方式。

三角形面形成的物体：

v 定义 8 个点，vn 定义 6 个面的法线（图中有冗余）、vt 定义 12 个纹理坐标（每个面四个点的纹理坐标，中间会有共用的），f（face）定义三角形之间的连接关系（第一个参数是顶点，比如图中第一行使用第 5、1、4 三个顶点形成三角形，第二个参数是三个顶点的纹理坐标，第三个参数是指三个顶点的法线）

​​

曲线

相机的运动曲线，三维建模模型的运动曲线、定义字体的控制点

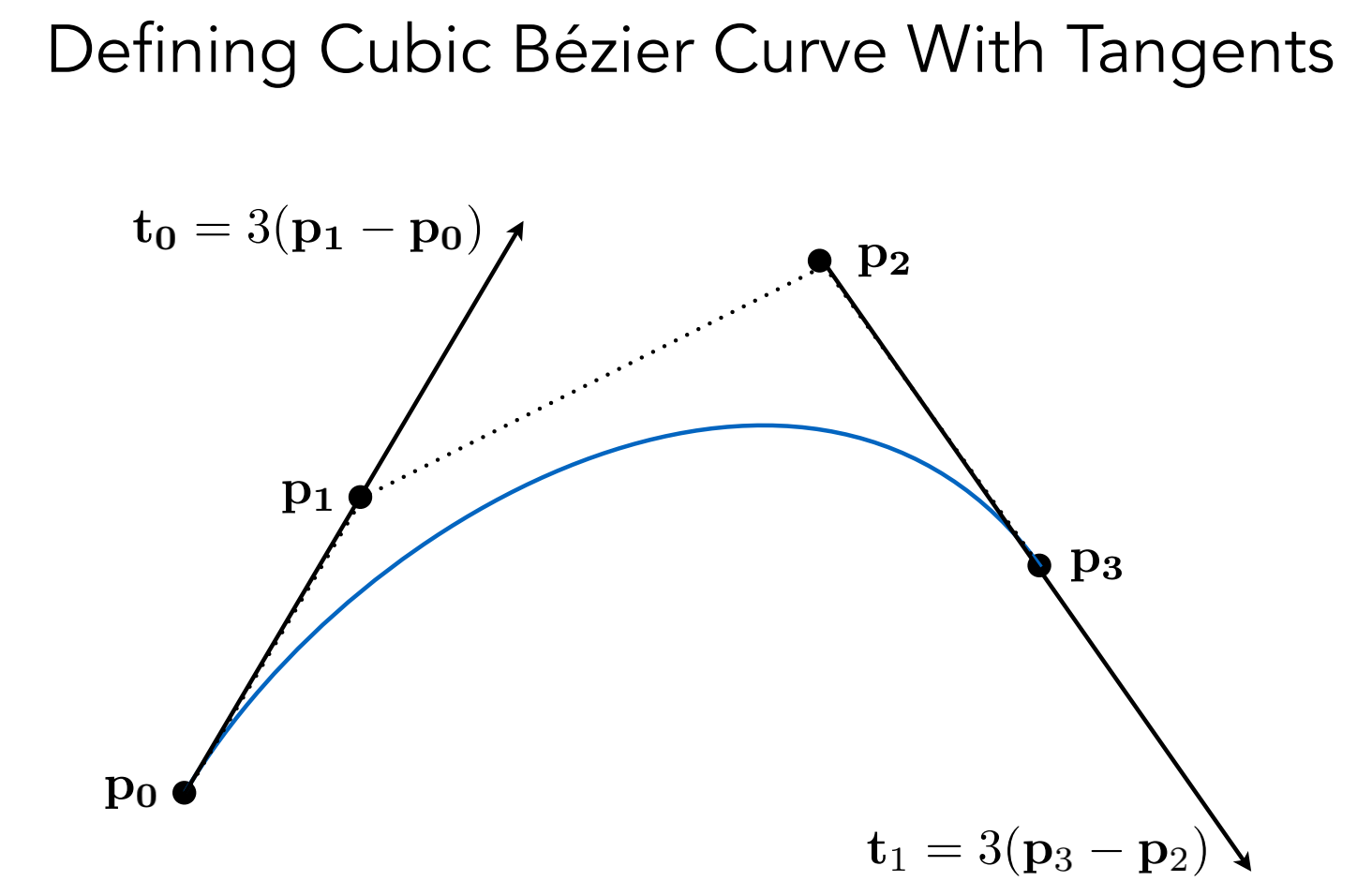
贝塞尔曲线（用一系列控制点来定义曲线）

曲线的起点在 P0、开始的方向是 P0P1，曲线的终点是 P3，结束的方向是 P2P3

​​

de Casteljau 算法

给任意一个时间 t，计算贝塞尔曲线在时间 t 的位置

​​​​

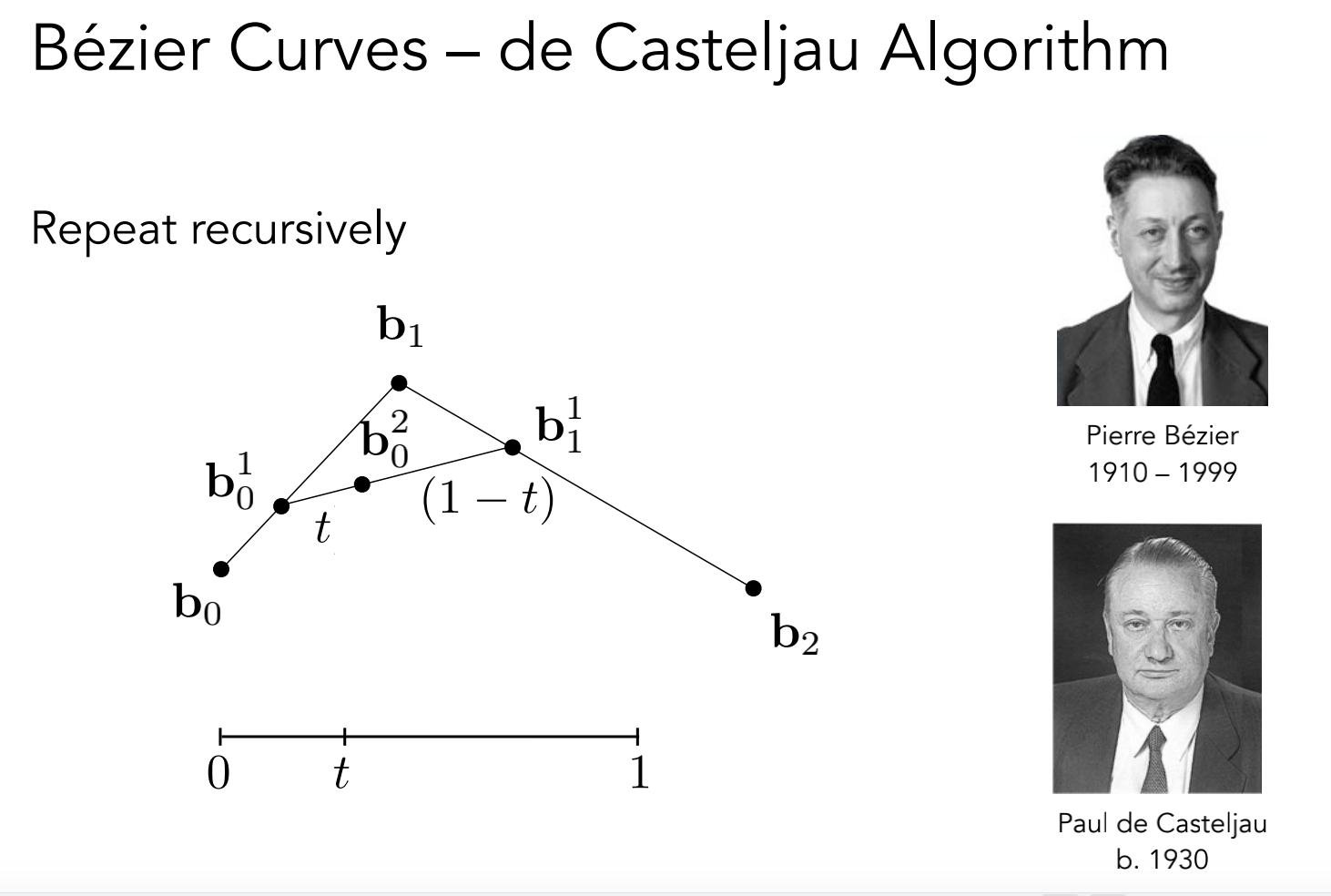
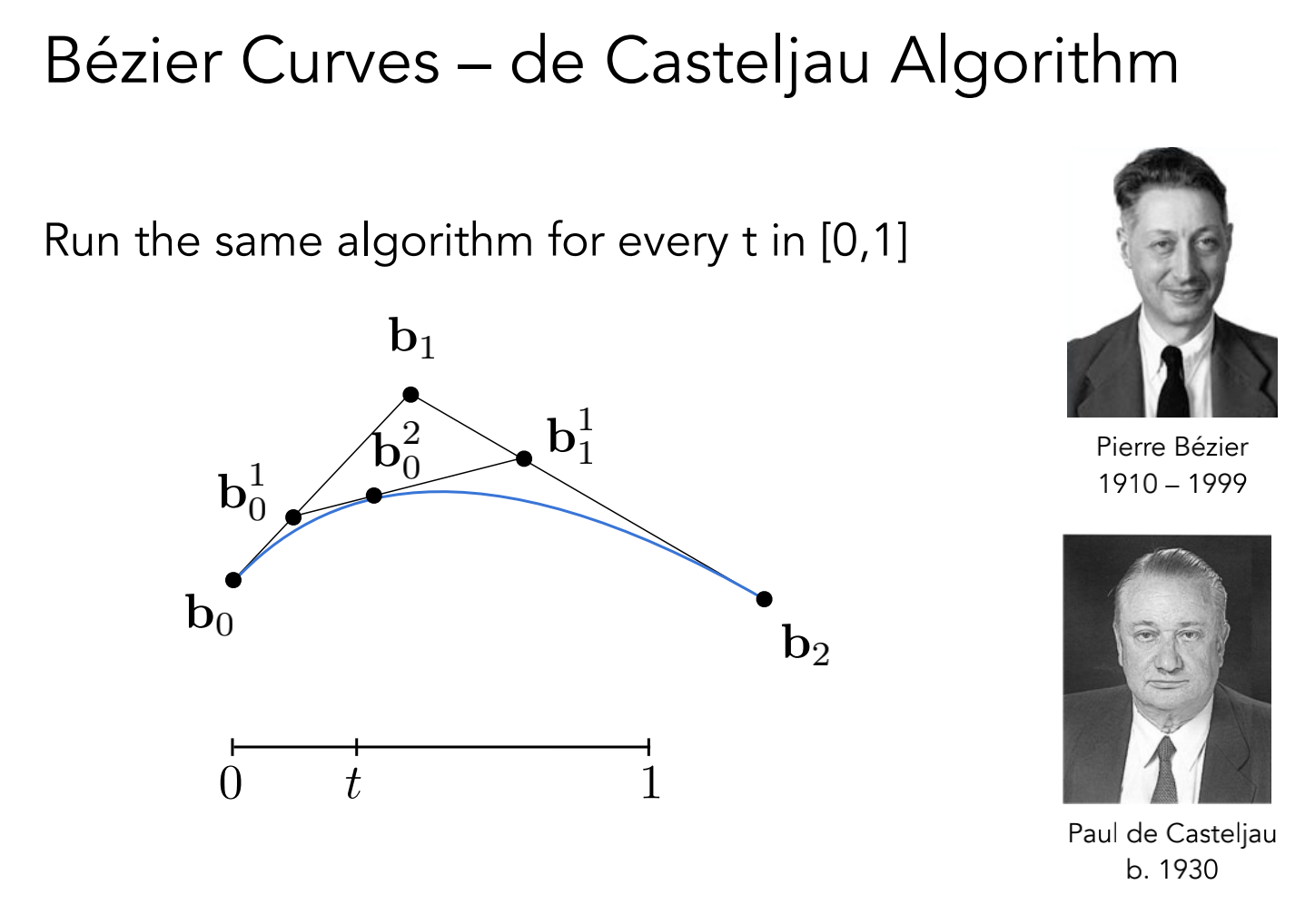
是一个递归的过程

​​​​​​

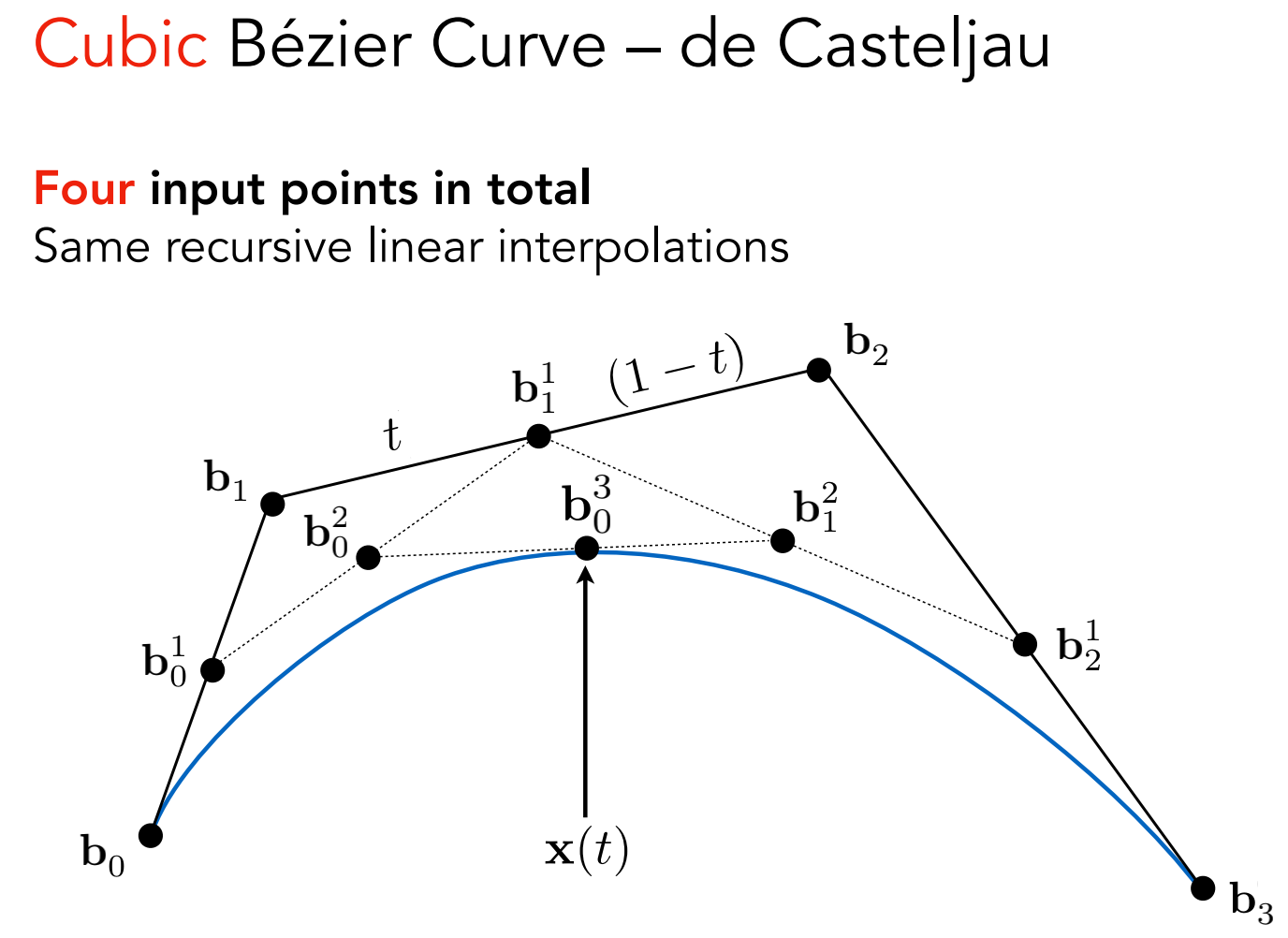
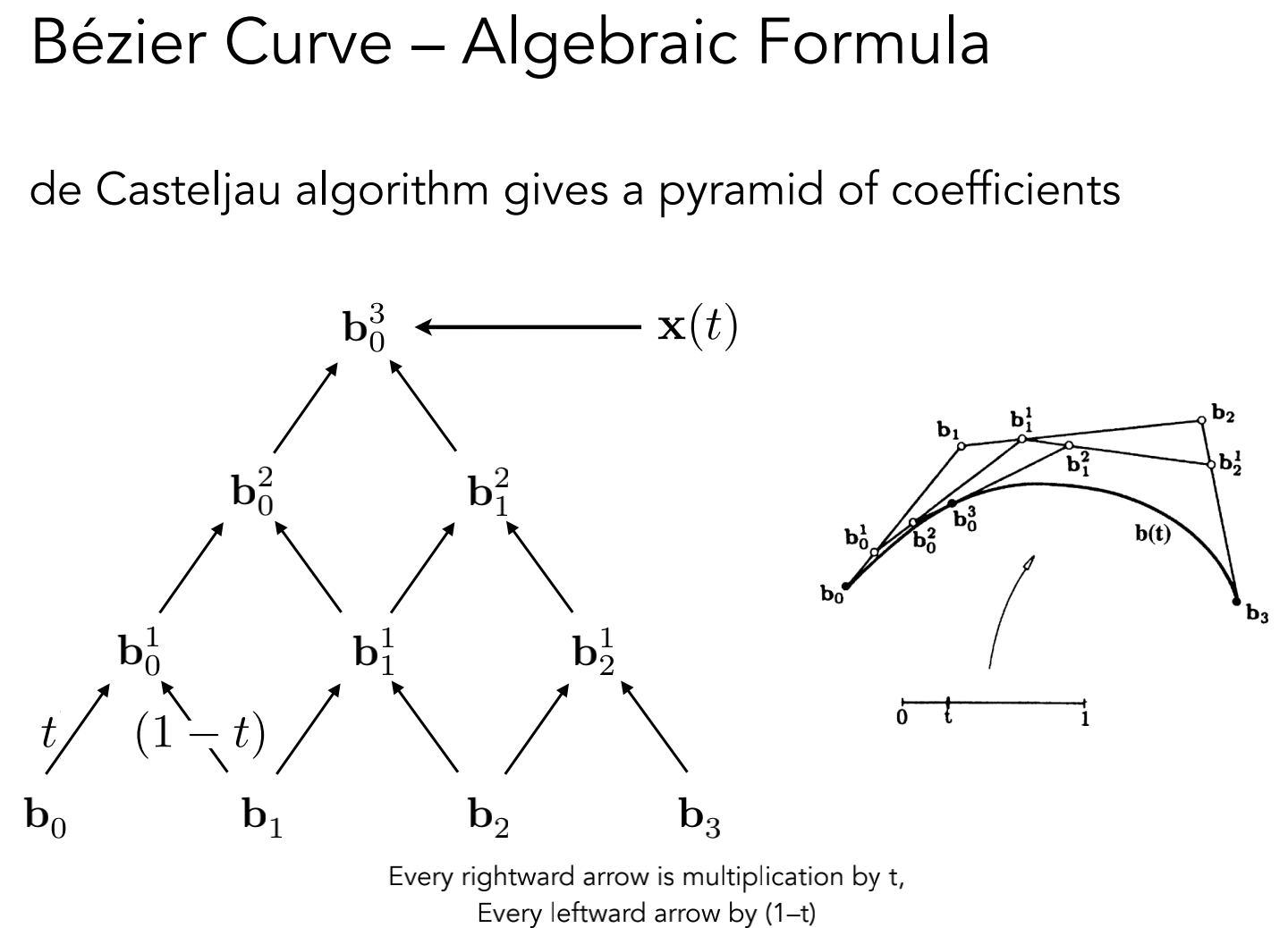
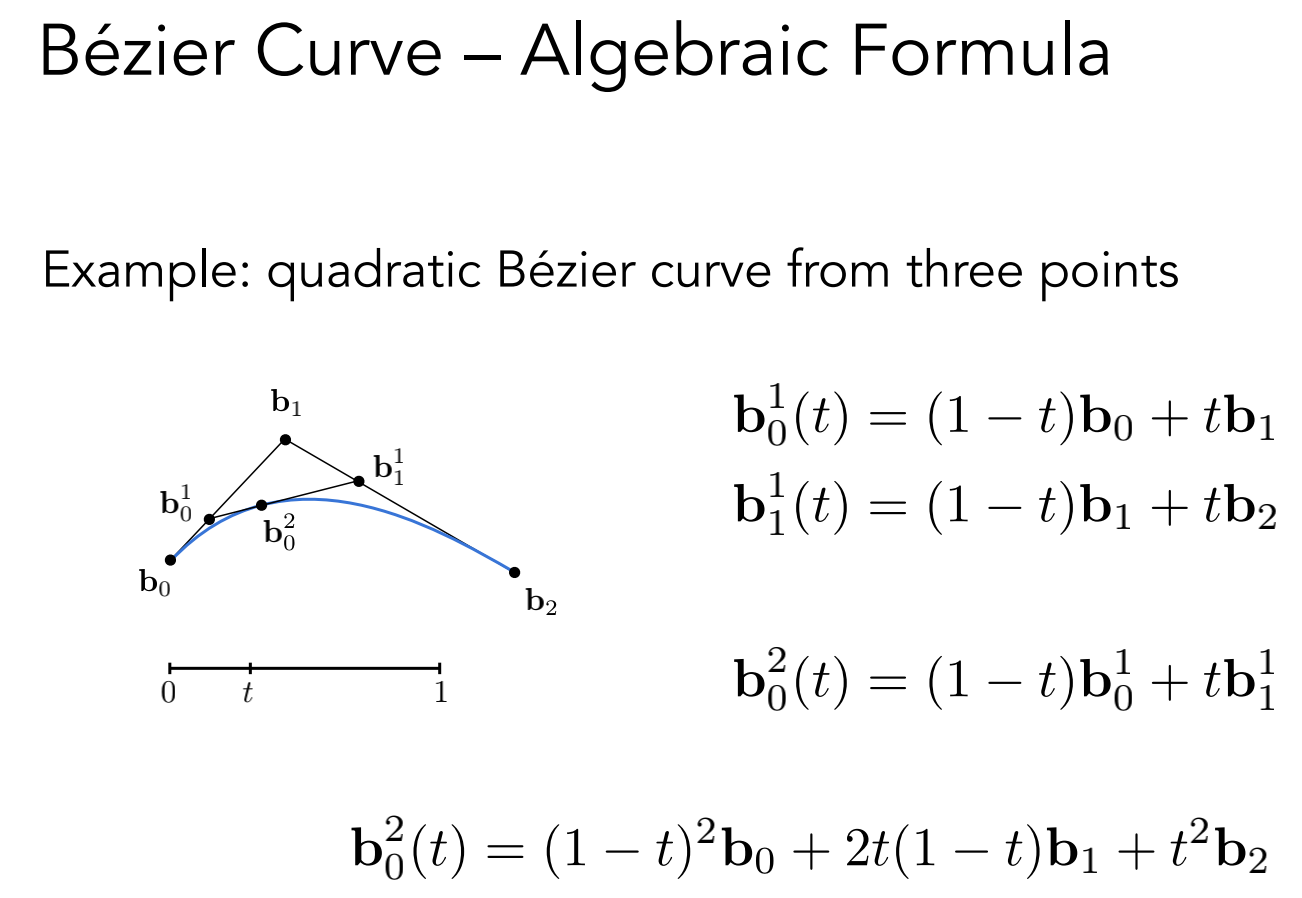
n 阶贝塞尔曲线可以表示为控制点的线形组合，系数就是一个和时间有关的多项式，被称为 Bernstein 多项式

​​

三维空间中同样可以用 Bernstein 多项式

​​

Bernstein 多项式就是 1 的多阶展开，所以在坐标轴上画一条竖线，经过的每个点的 y 轴加起来的值都等于 1

​​

贝塞尔曲线的性质：

1.起点和终点固定

2.切线方向固定

3.对曲线的顶点、控制点做仿射变换后，再画贝塞尔曲线，和对原始贝塞尔曲线做仿射变换后得到的曲线是一样的；但对投影不是这样

​​

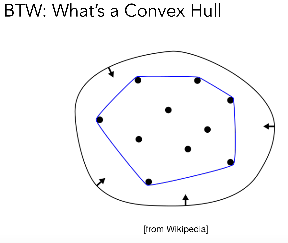
4.秃包性质：任何一个贝塞尔曲线肯定在控制点形成秃包之内。比如如果给一堆控制点都在一条直线上，那这个贝塞尔曲线一定是这条线自己。

秃包：能包围给定的几何形体的最小的凸多边形

想象有一堆钉子，在最外层的钉子上绑一个橡皮筋，橡皮筋围成的形状就是秃包

​​

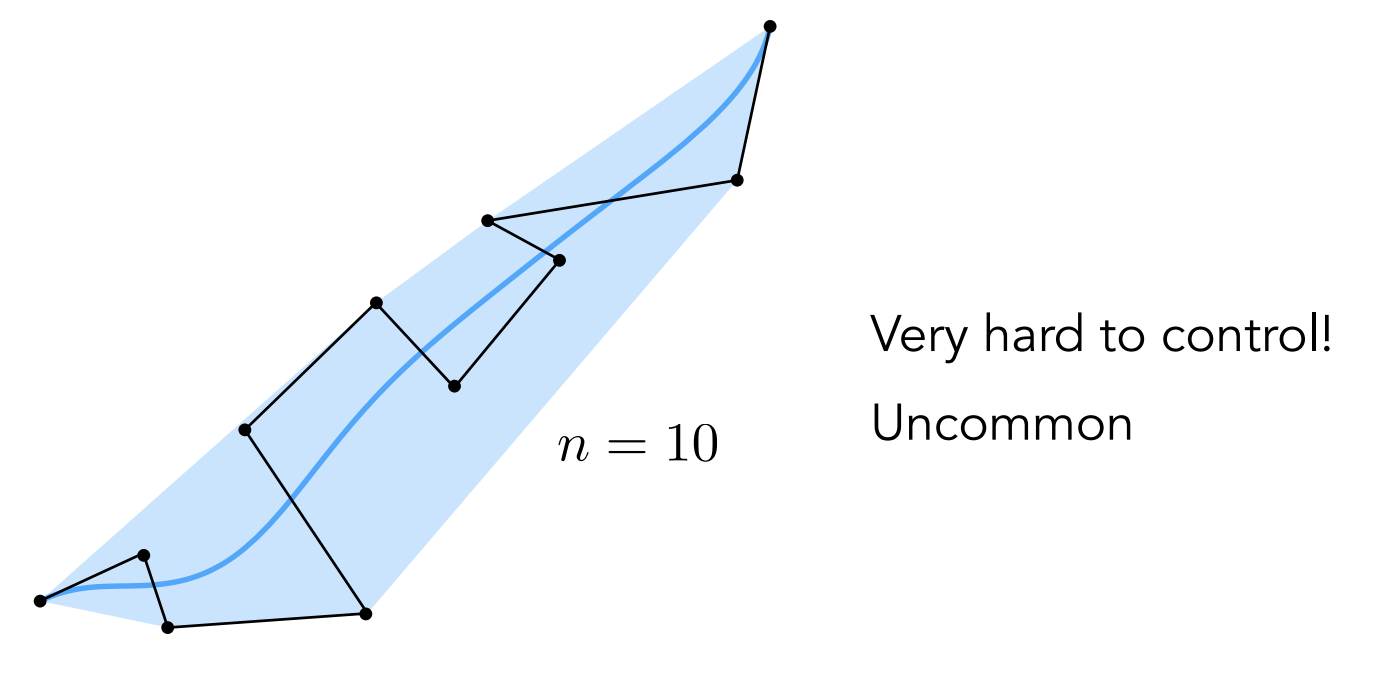
Piecewise 贝塞尔曲线

控制点多的时候不好控制，逐段定义贝塞尔曲线，再连起来。一般是每四个控制定义一条贝塞尔曲线。

​​

几何上两条曲线都通过一个点，第一段的终点等于第二段的起点叫做 C0 连续

​​

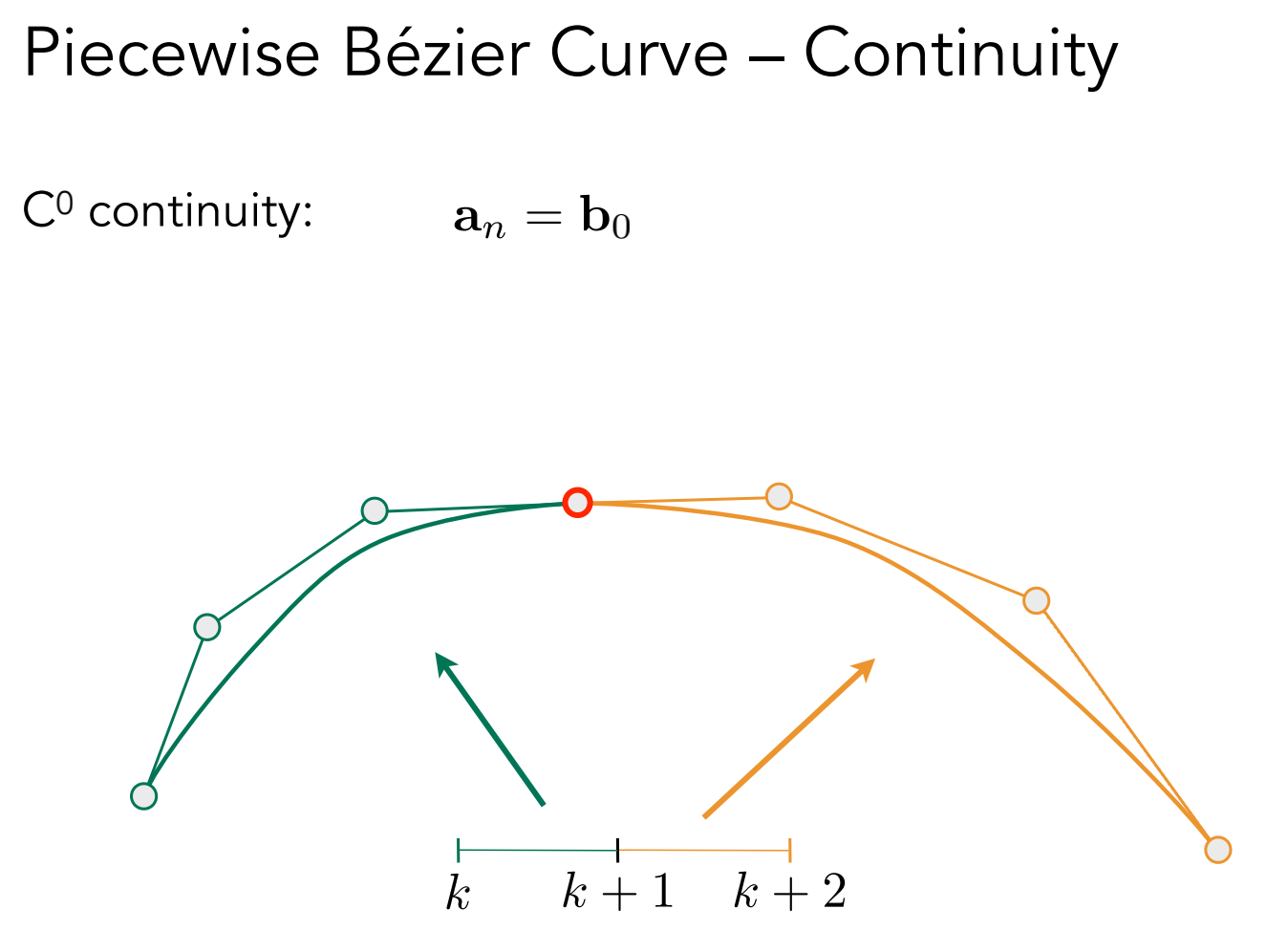
第一段终点控制点连线和第二段起点控制点的连线大小一致，方向相反，C1 连续（一阶导数连续）

​​

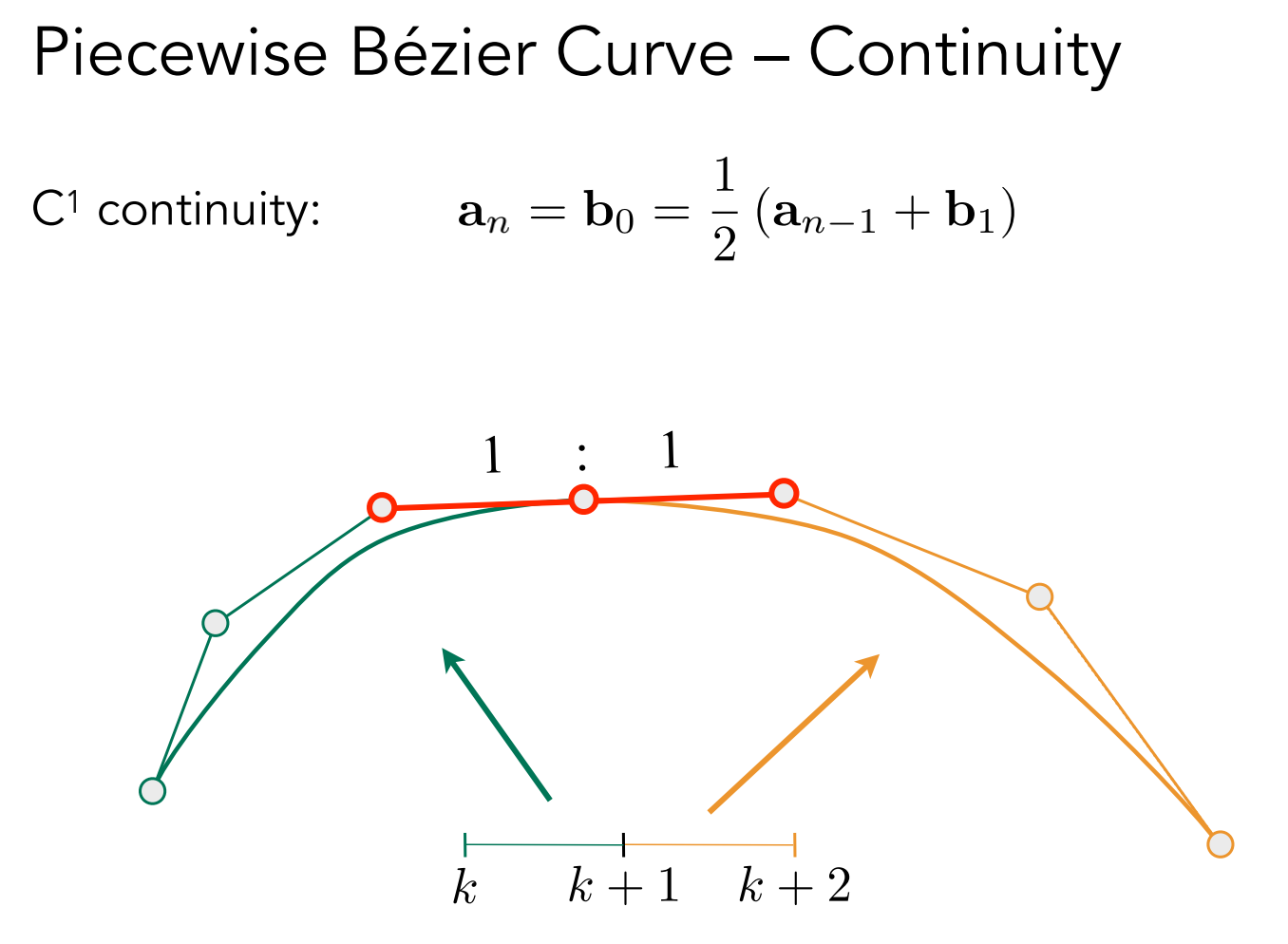
Spline 曲线（样条）

由一组控制点控制的曲线，能满足一定的连续性

B-Spline basis splines（奇函数样条，由于不同的函数组合起来形成新的函数）

• 用 Bernstein 多项式在时间 t 几个不同的项对不同的控制点做加权平均
• 用控制点的位置对 Bernstein 多项式进行加权

B-Spline 是对贝塞尔曲线的扩展，可以实现局部性，比如改变一个控制点，只影响一定范围内的曲线。

本节课不深入学习 B 样条

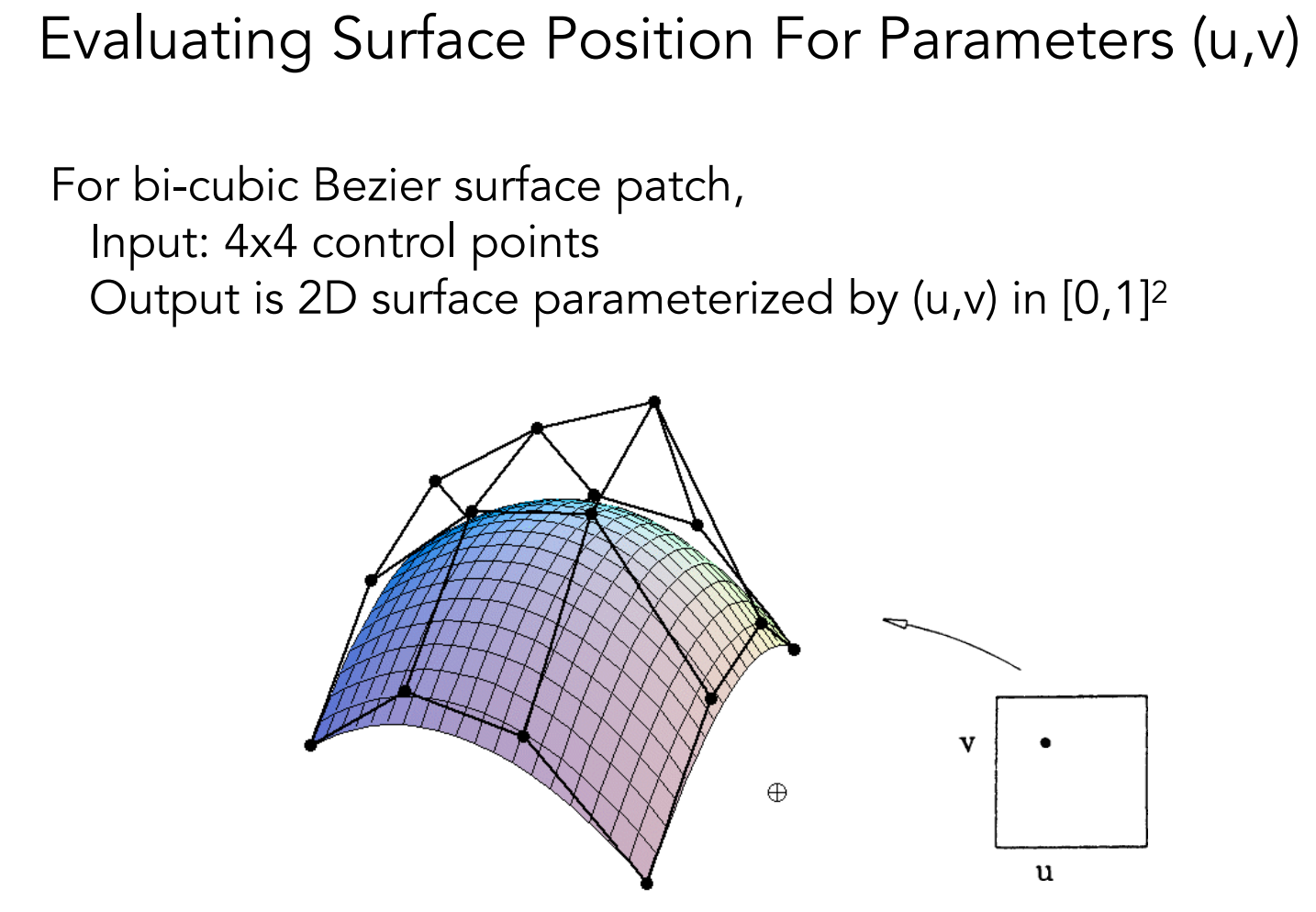
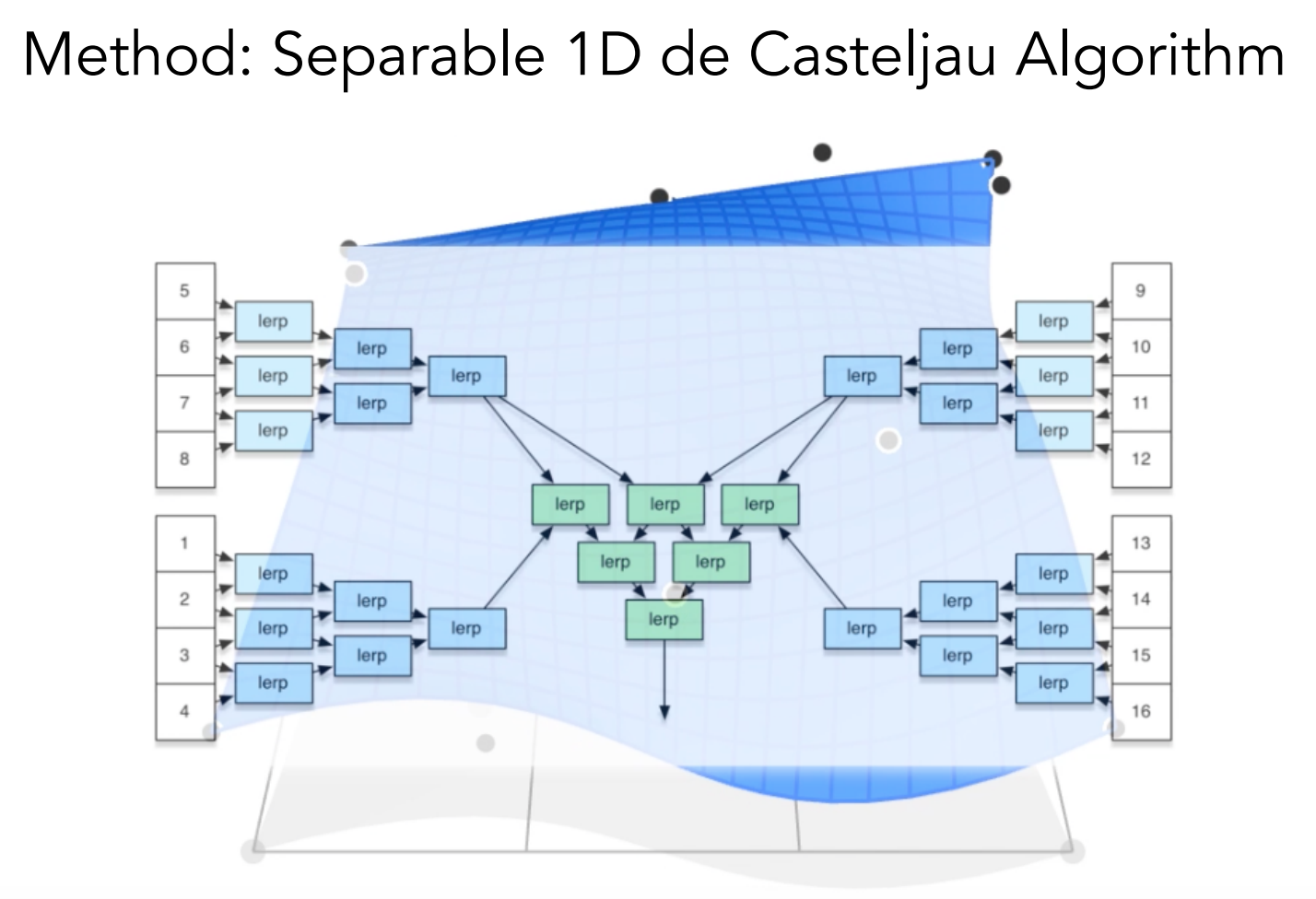
贝塞尔曲面

贝塞尔曲线得到贝塞尔曲面

4✖️4 控制点，双线性插值

用时间 u 先确定一个方向的四个控制点，再用时间 v 确定曲面上的一个点

​​​​​​

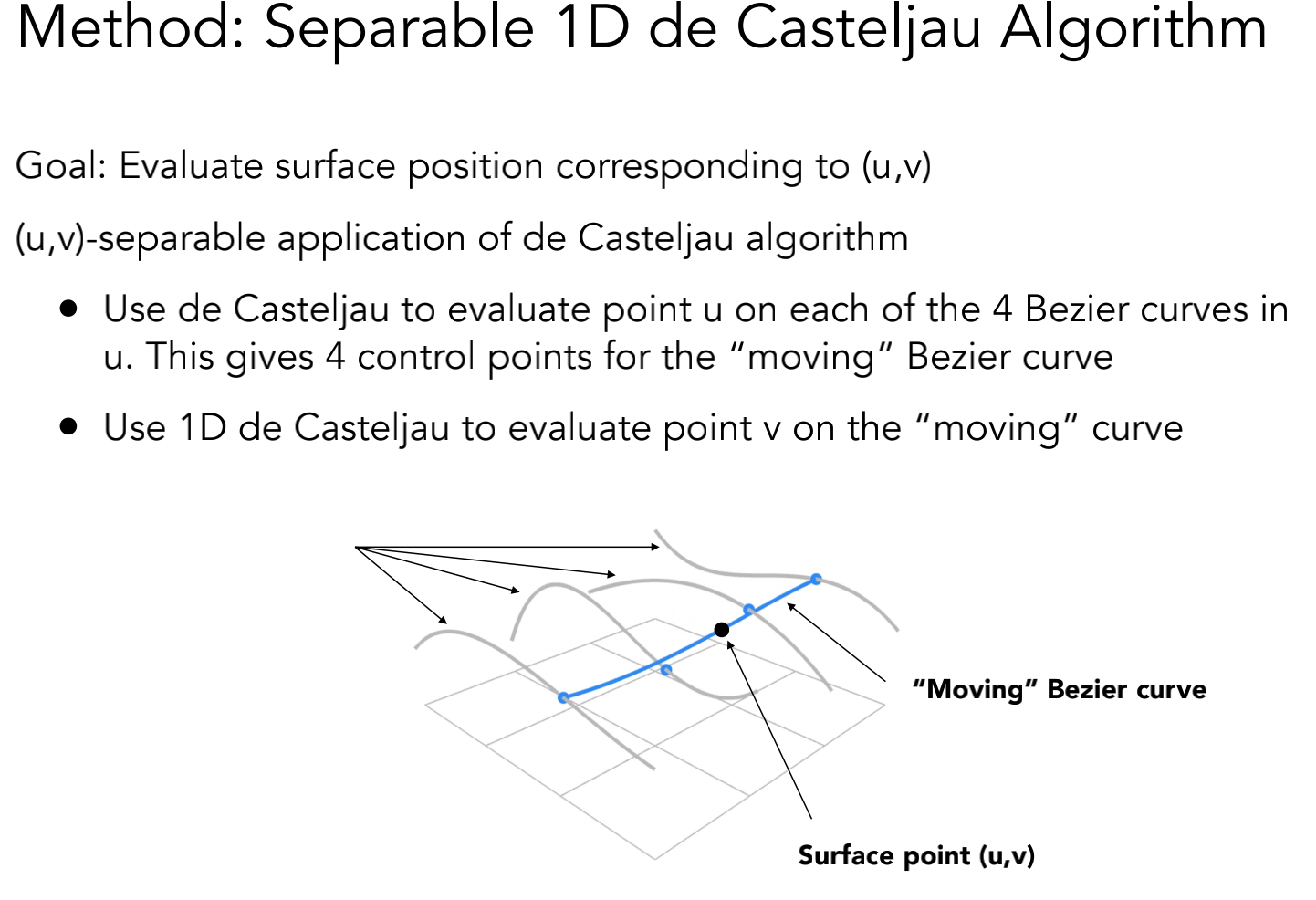
Mesh Operations：几何处理

• 网格细分

• 网格简化

• 网格正规化（让三角形不要出现特别尖的三角形）

  ​​

‍