第六章:反走样与深度缓冲
反走样和深度缓冲
上节课提到:
MVP变换后,把得到的[-1,1]3区域映射到屏幕上。光栅化的思想:用像素的中心对三角形的可见行函数进行采样。
本节课学习的主要内容:
- 反走样
- 采样理论
- 实际图形学中怎么做反走样
- 可见性/遮挡
- 深度缓冲
采样在图形学中是一种广泛的做法:
比如光栅化的过程,在屏幕空间用一些离散的点采样
照片,所有到达感光元件所在平面的光学信息离散成图像上的像素
采样可以发生在不同的时间,比如视频、动画是把一系列的图在不同时间进行采样。
采样artifacts(瑕疵):
- 锯齿-空间中采样
- 摩尔纹(照片奇数行和技术列去掉),拿手机拍屏幕-不同位置采样
- 顺时针转的轮子看起来在逆时针旋转-人眼在时间中采样跟不上运动的速度
采样artifacts的本质:
信号的变化太快了,以至于采样的速度跟不上信号变换的速度。
反采样:
采样前做一个模糊(滤波)
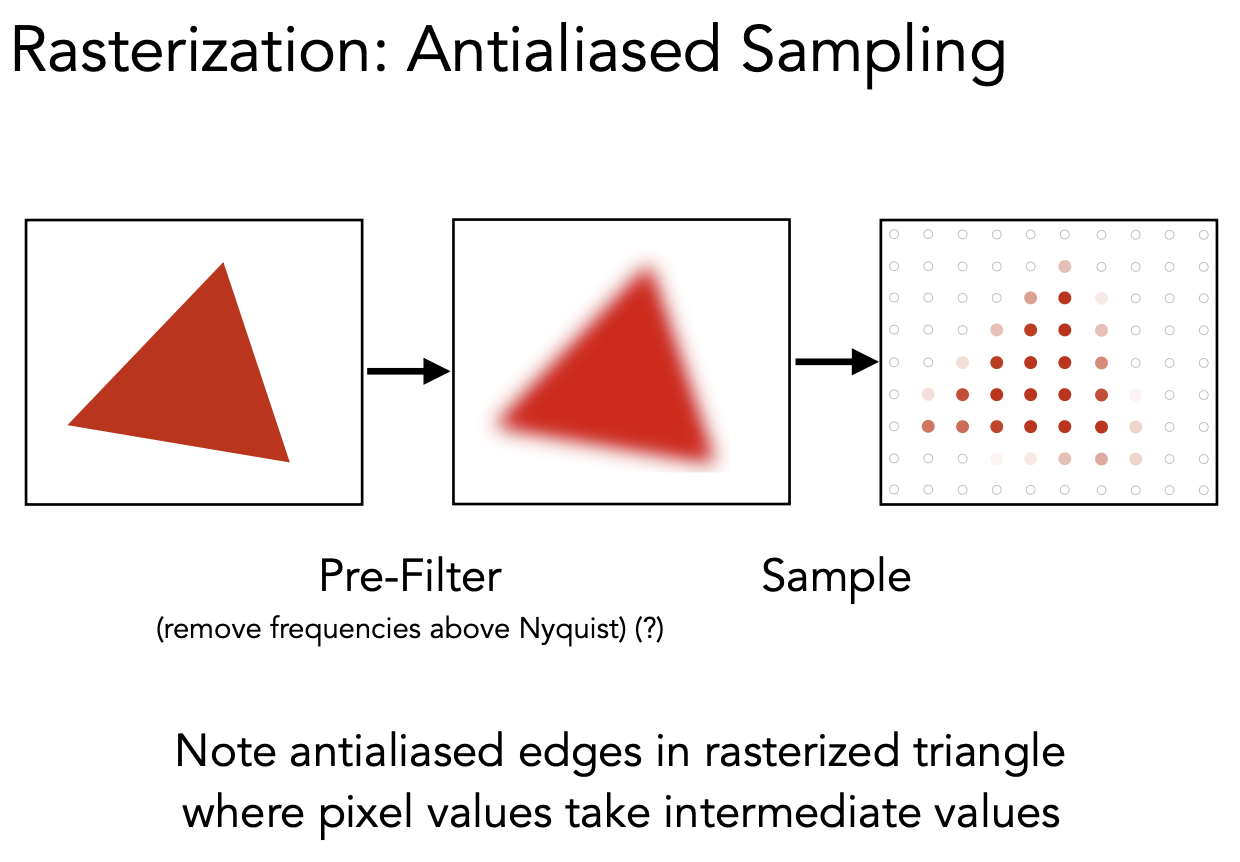
可以先模糊(滤波)再做采样,但不能先采样再模糊。
为什么采样速度跟不上信号变换的速度会造成采样artifacts?
频域
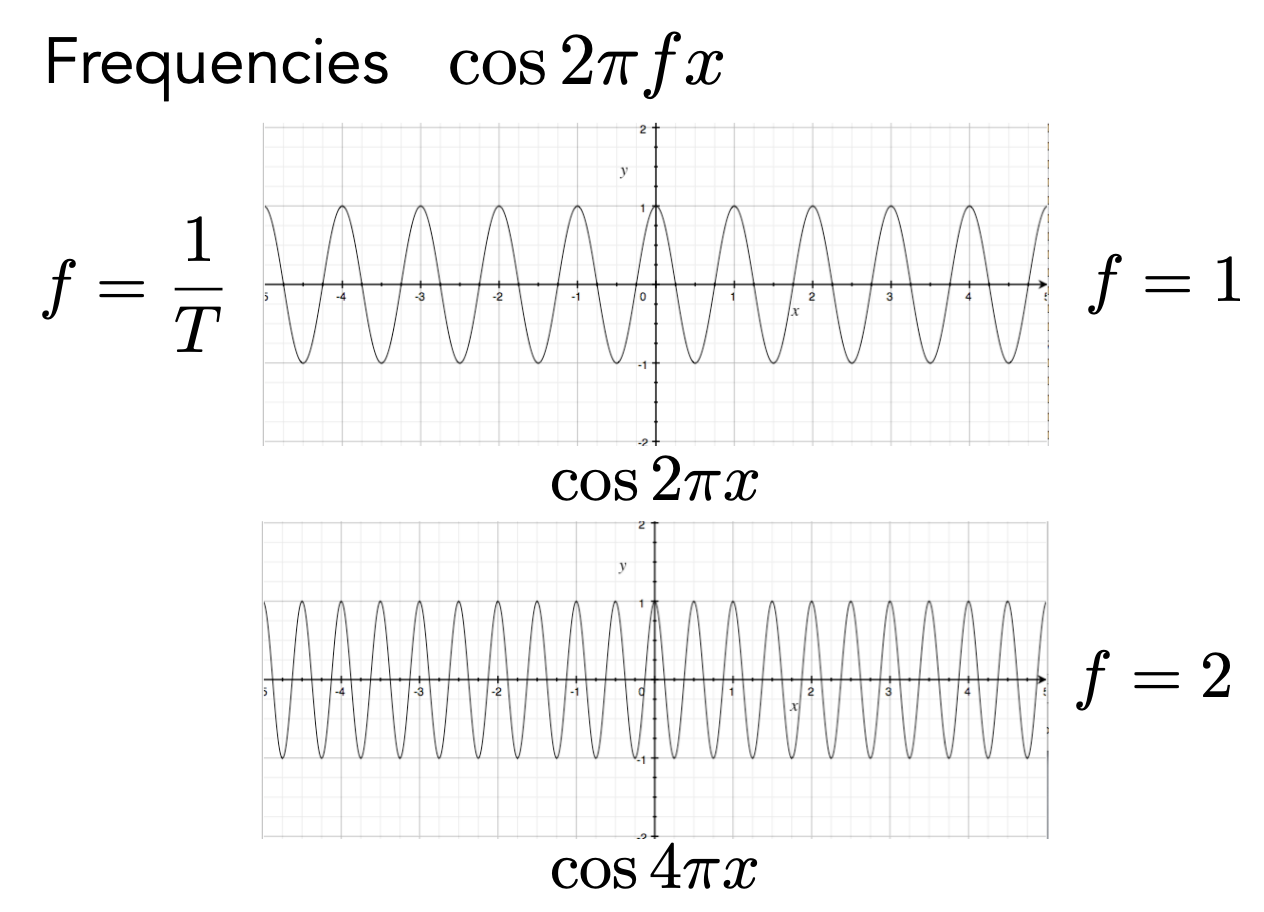
用f定义余弦波变换的速度,周期是频率的倒数
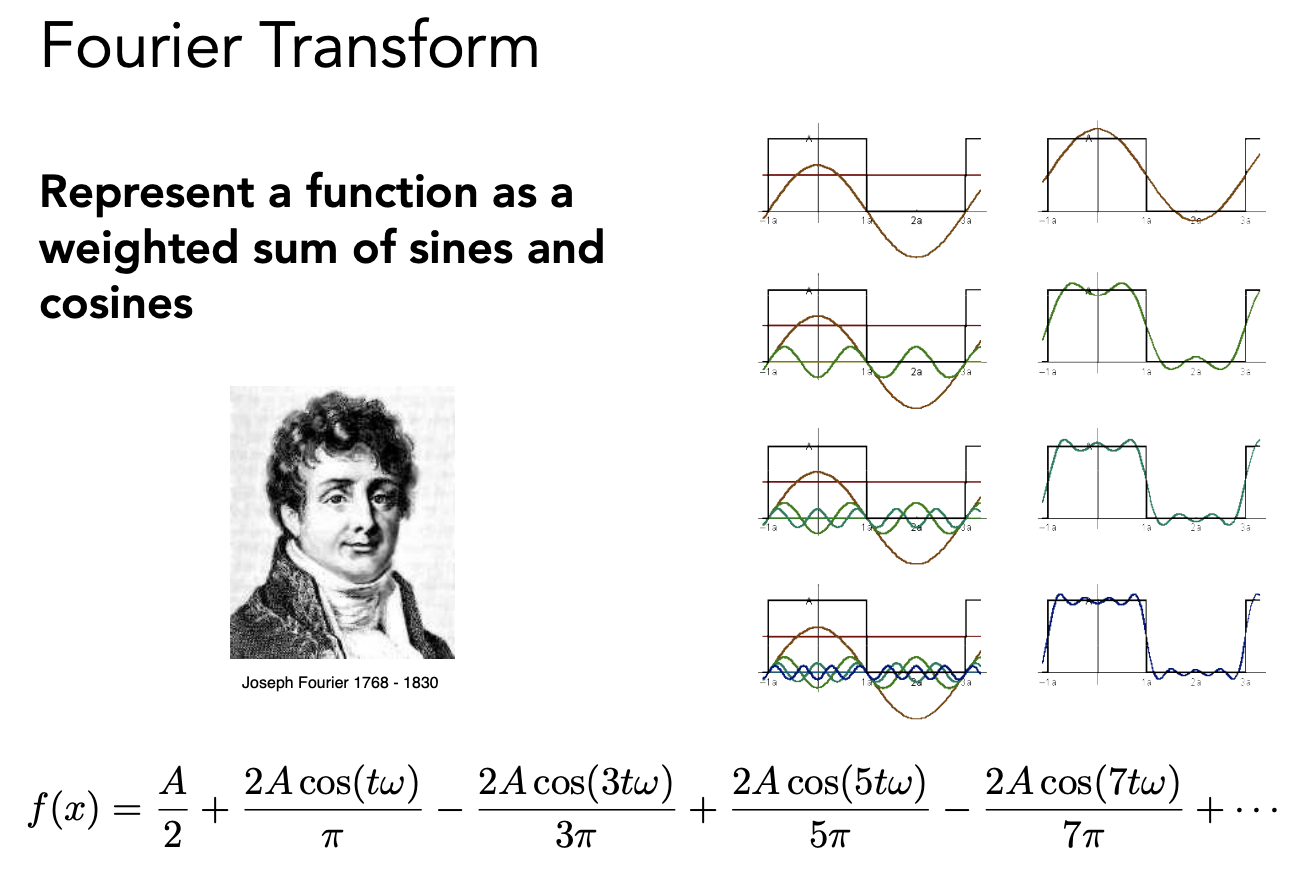
傅立叶级数展开
任何一个周期函数都可以写成正弦、余弦的线性组合加常数项。
傅立叶变换:把一个函数变成另一个函数
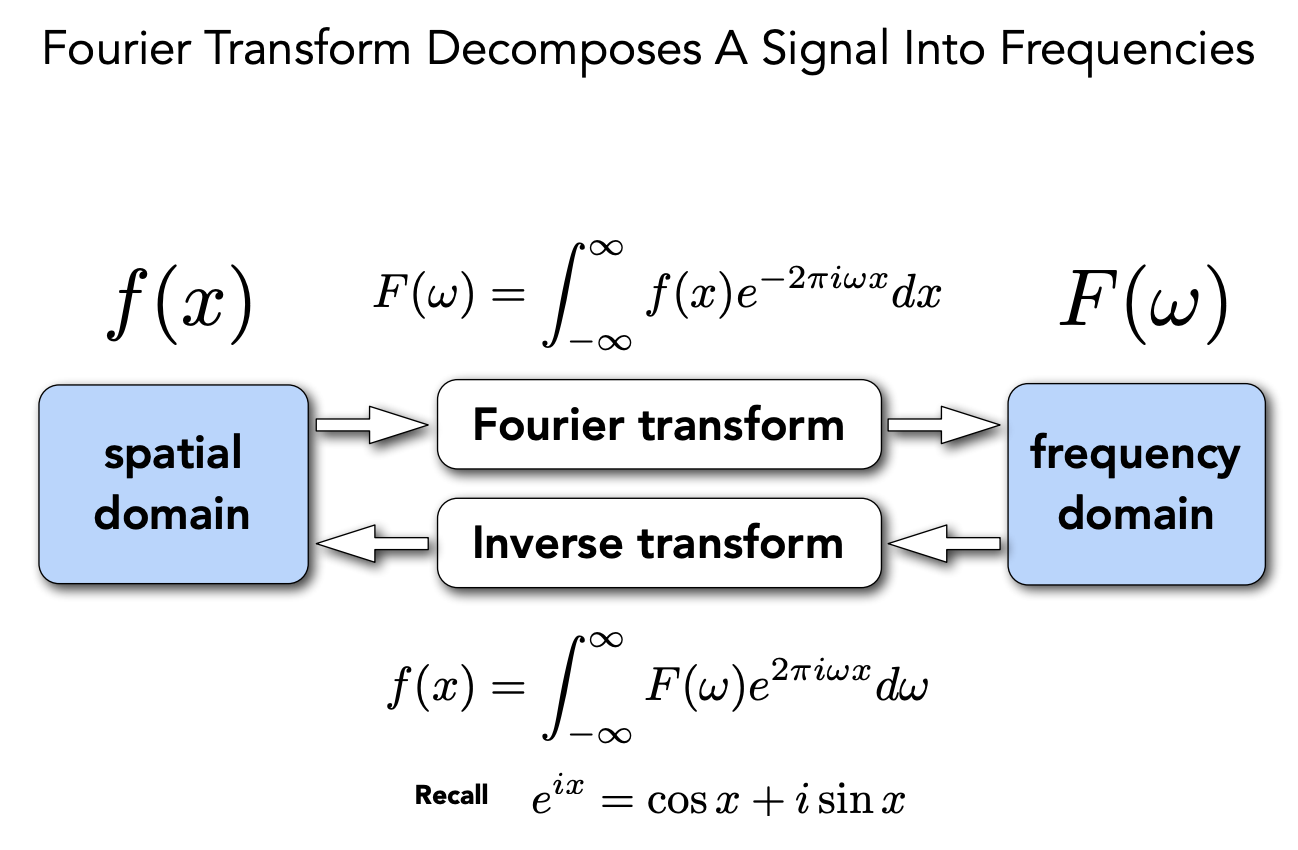
傅立叶变换就可以把函数变成不同频域的段并显示出来。
相同的采样点,原函数频率越高,采样越不准确。
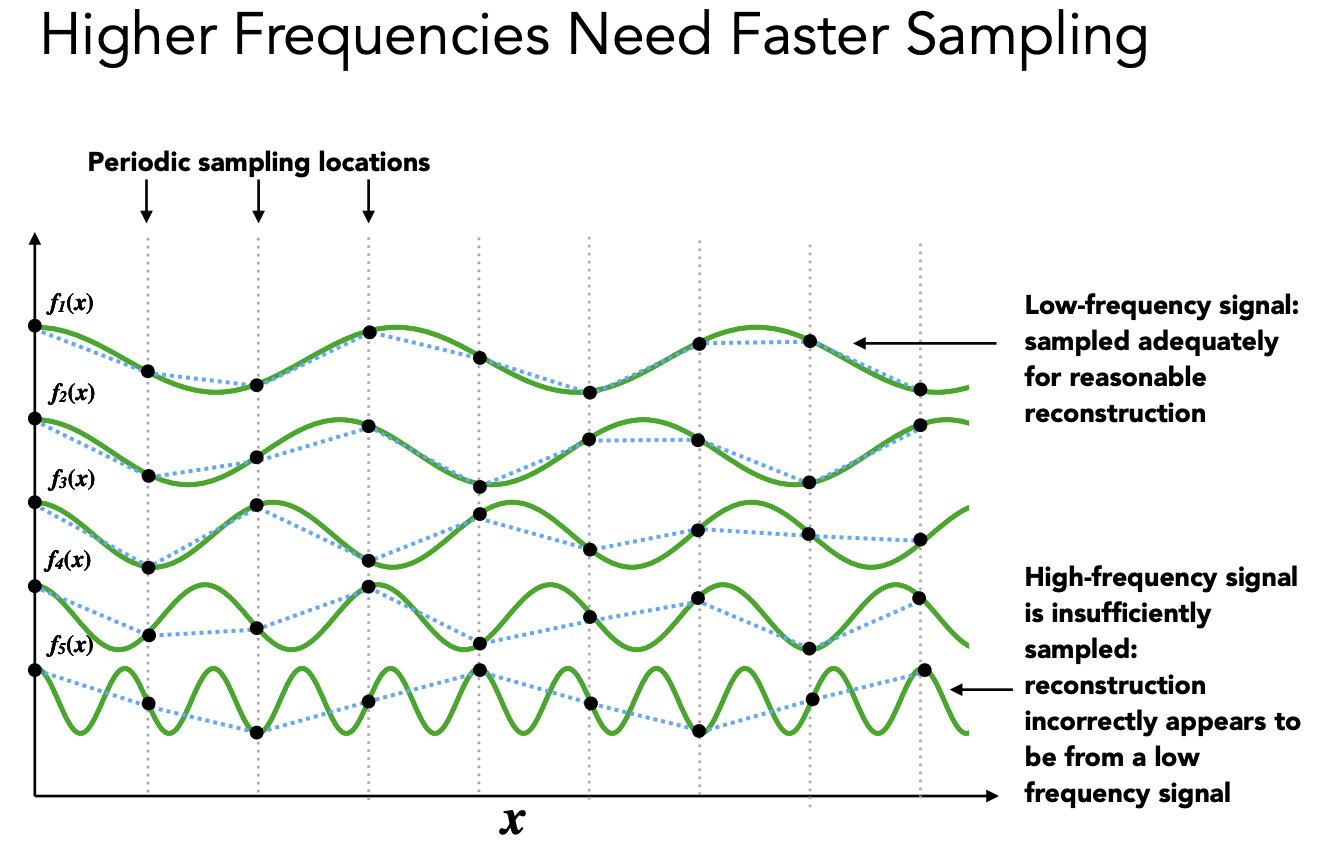
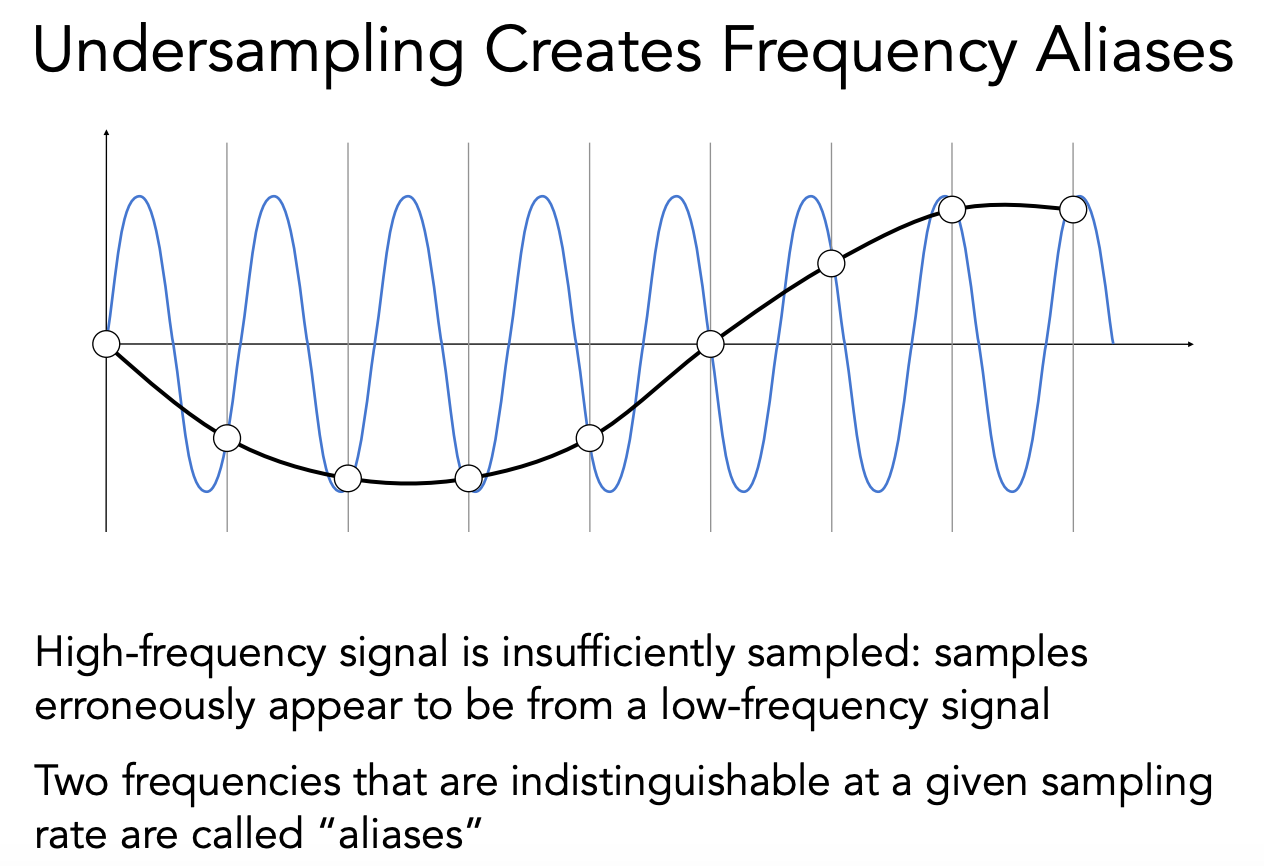
同样一个采样方法采样两种不同频率的函数,得出的结果无法区分,就叫做走样
滤波
把某个特定的频率去掉,看信号会发生什么样的变化。
傅立叶变换可以把一个函数从时域(把空间不同的位置也看作时域)变到频域。
把中心看作低频区,周围是高频区,用亮度表示在不同频率的位置上有多少信息,如下图大多数信息集中在低频上:

为什么右侧的图像会有两条白线,因为处理图片信号的时候,会把图片视作周期性变化(类似于图片水平方向和竖直方向依次叠放了多张图),由于图片并不是真的周期变化,到达图片边界时,会发生剧烈的信号变化,产生极其高的高频。
傅立叶变换可以让我们看到一张图像在不同的频率长什么样,即得到一张图像的频谱。
假如去掉低频的信息,再做傅立叶逆变换,会得到图像内容的边界,因为在边界处会发生剧烈的变化,即频率比较高。这种滤波称为高通滤波,即这种滤波器只有高频信号能通过。
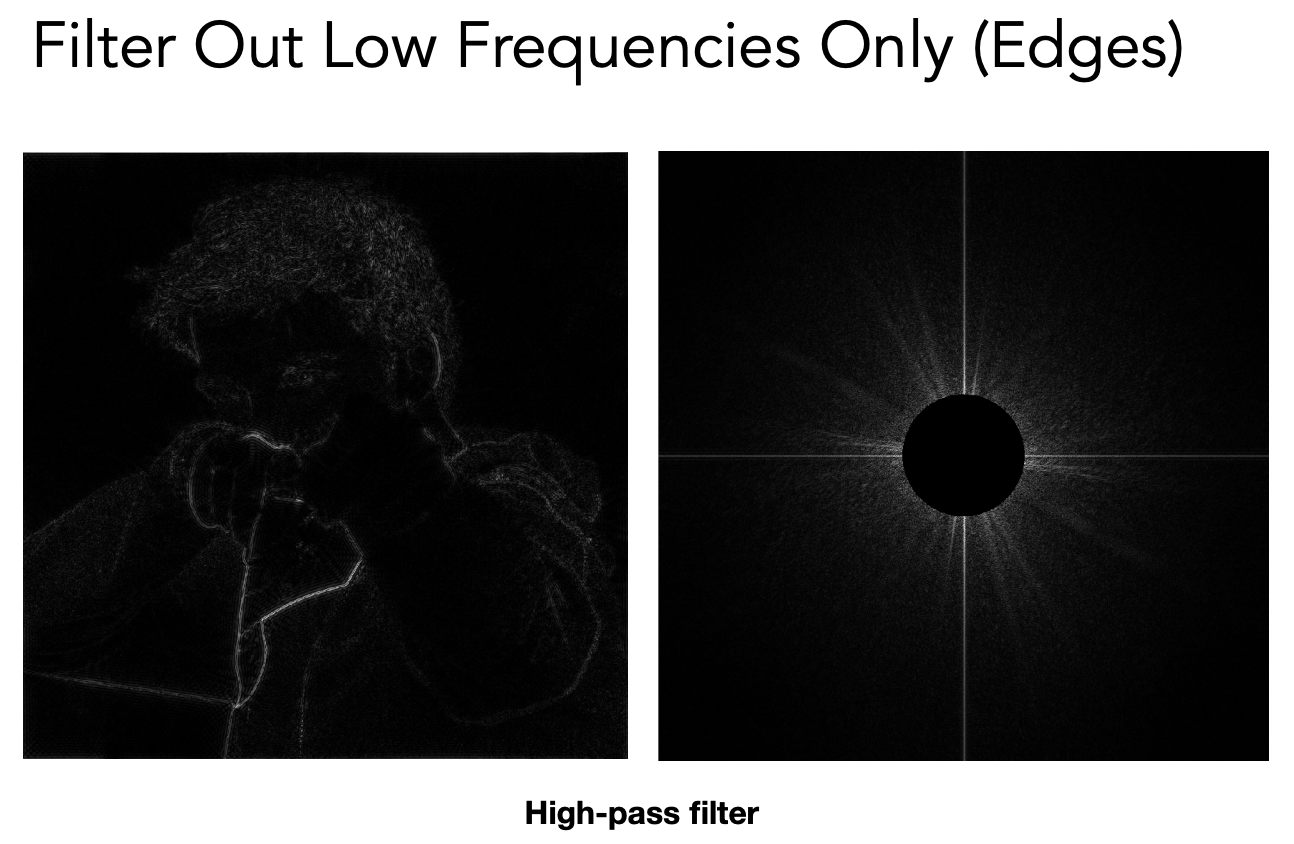
假如只留下高频的信息,去掉低频的信息,再做傅立叶逆变换,会得到一张(边界)比较模糊的图。这种滤波称为低通滤波。

滤波=平均=卷积
卷积(图形学上定义:滑动过滤器,做点乘,得到一个加权平均值)
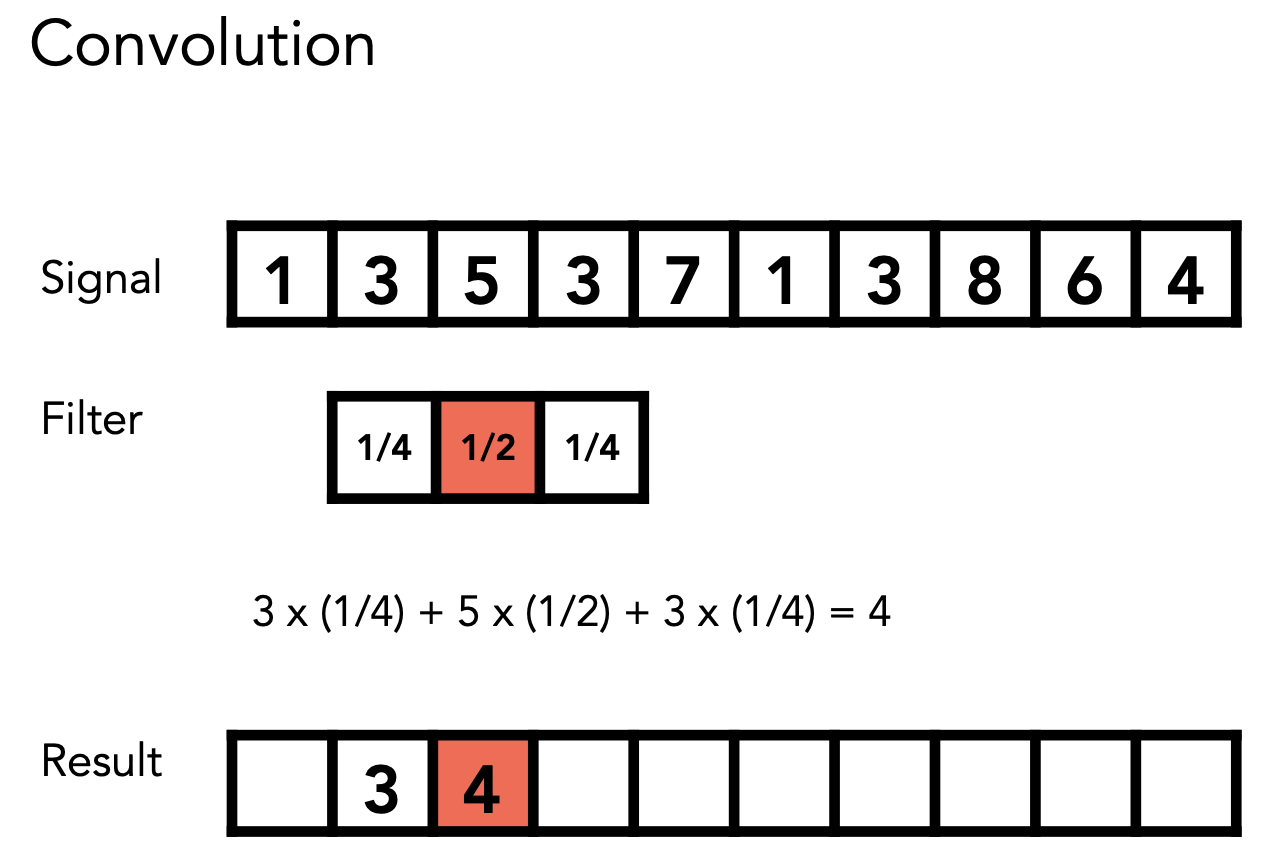
卷积定理:时域上对两个信号做卷积,对应频域上两个信号做乘积。时域的卷积等于频域的乘积,时域上的乘积等于频域上的卷积:
- 可以选择直接在时域上做卷积
或者先做傅立叶变换变到频域上,卷积核也做傅立叶变换到频域上,在频域上做乘积,乘积结果再做逆变换变回来。
![image]()
卷积核:
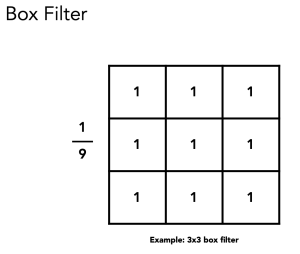
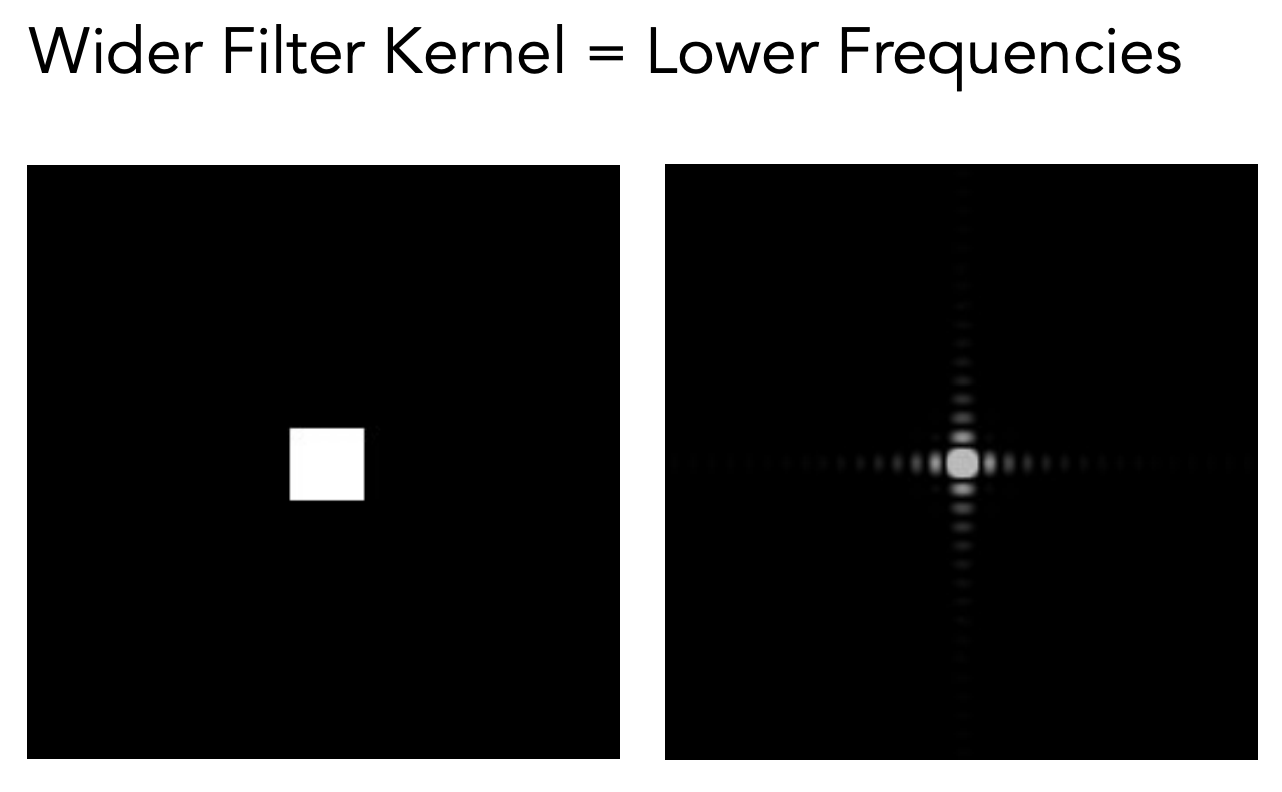
盒子越大,对应的频域范围越小,结果越模糊。盒子越小,频域范围越大。
从频率的角度上看采样:重复频域上的内容。
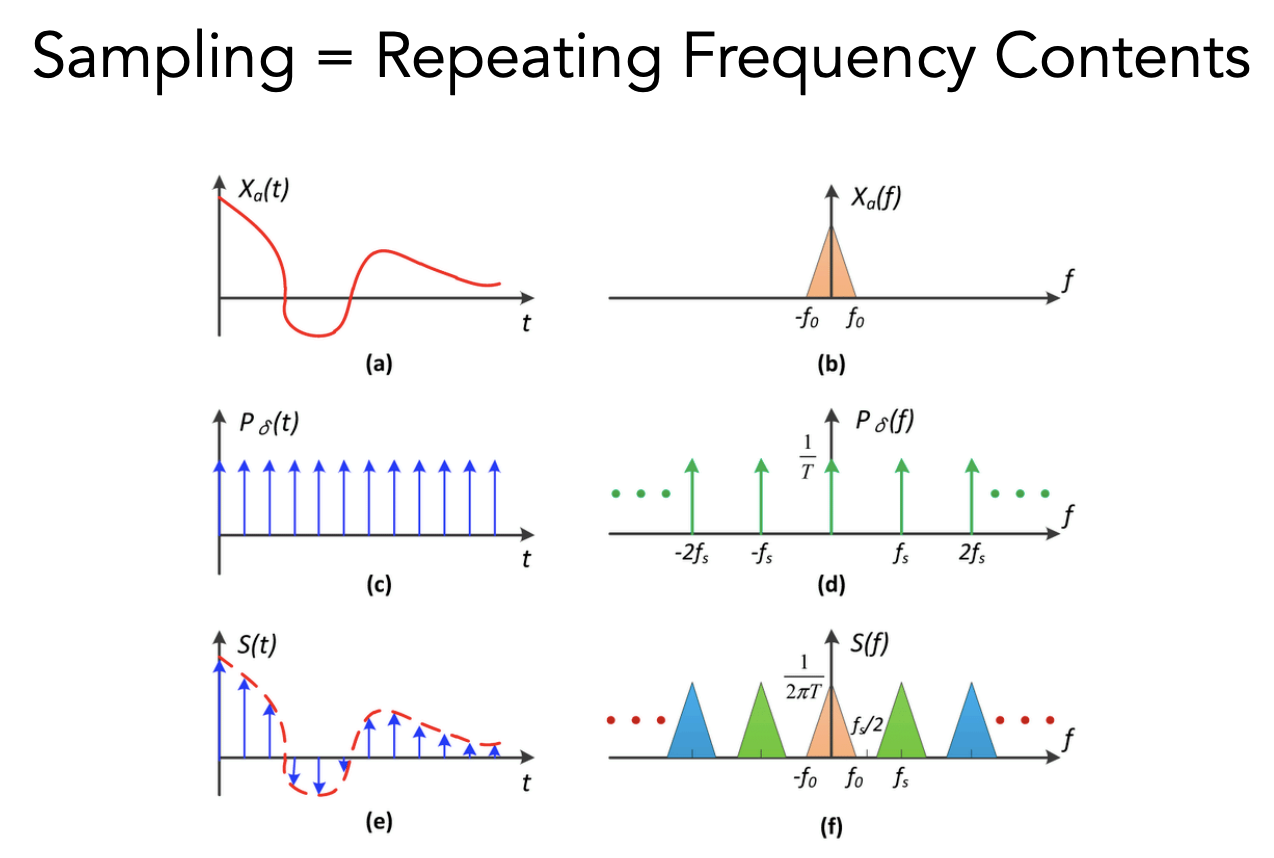
给一个原始信号(a),乘一个冲击函数(c)(只在某些固定位置有值,其他位置值为0),得到采样结果(e)。
把原始信号和冲击函数分别转换到频域上得到(b)和(d),做卷积得到(f)。
可以看出来:采样就是重复原始信号的频谱。
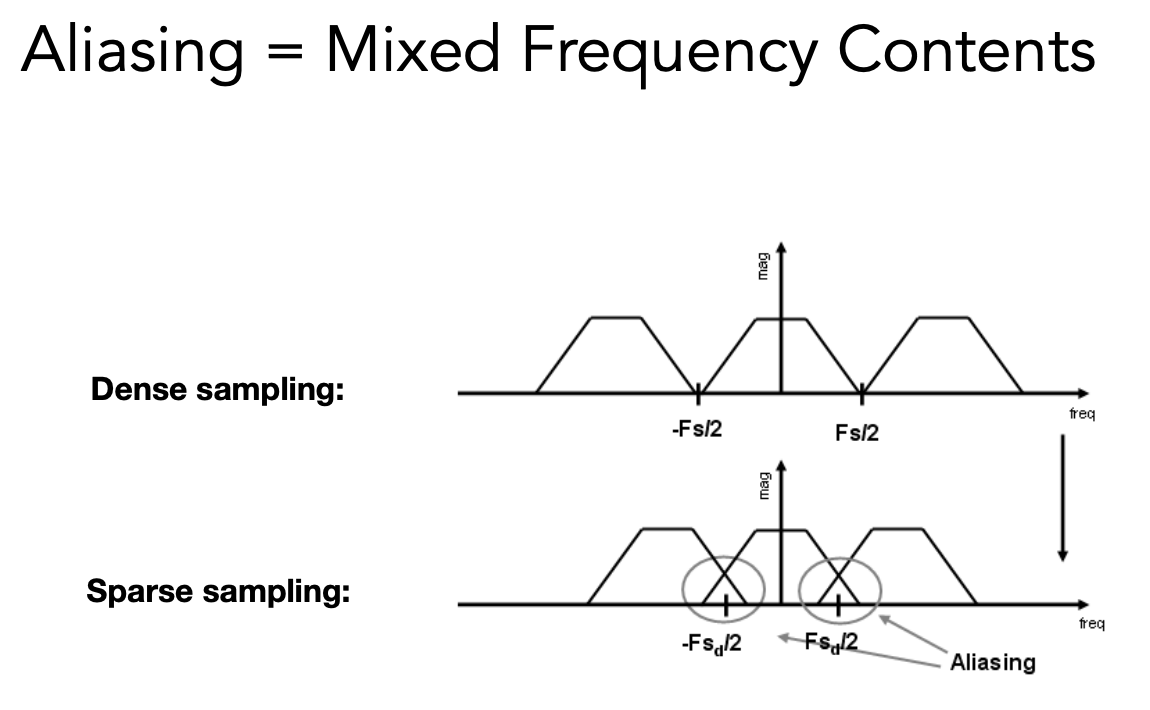
采样不同的间隔会引起频谱以不同的间隔移动,当采样率不足(采样不够快),原始信号复制粘贴的频谱间隔就很小。采样越稀疏,搬移频谱内容就越密集。原始信号和复制粘贴信号混在一起,这个时候发生了走样。
反走样:
1.增加采样率(高分辨率频幕)
2.先做模糊再做采样(先把高频信号拿掉,再采样,这个时候频谱覆盖面变小,再以原本间隔复制,就不会发生混别)
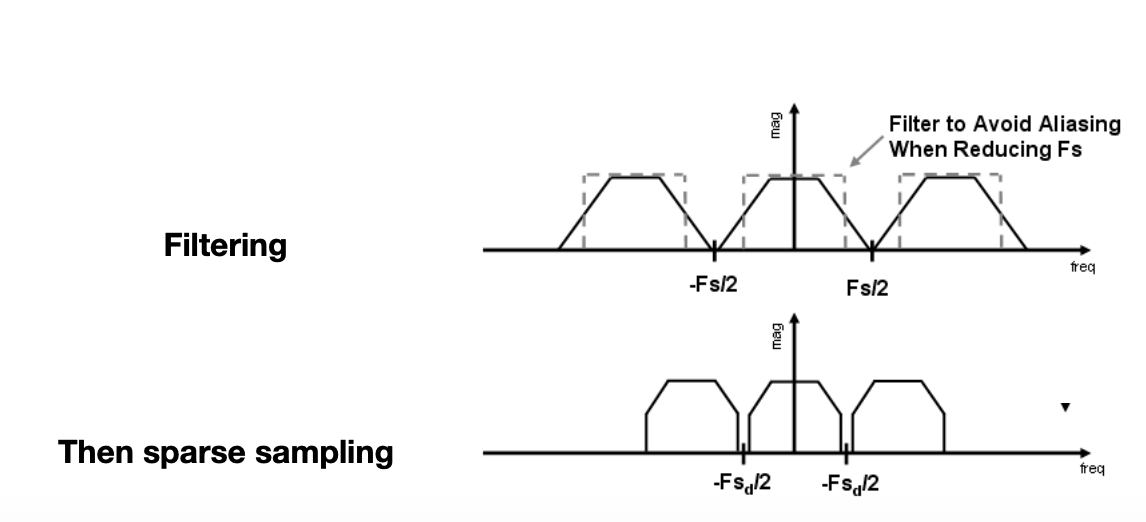
找一个一定大小的低通滤波器,对原来的频谱做卷积

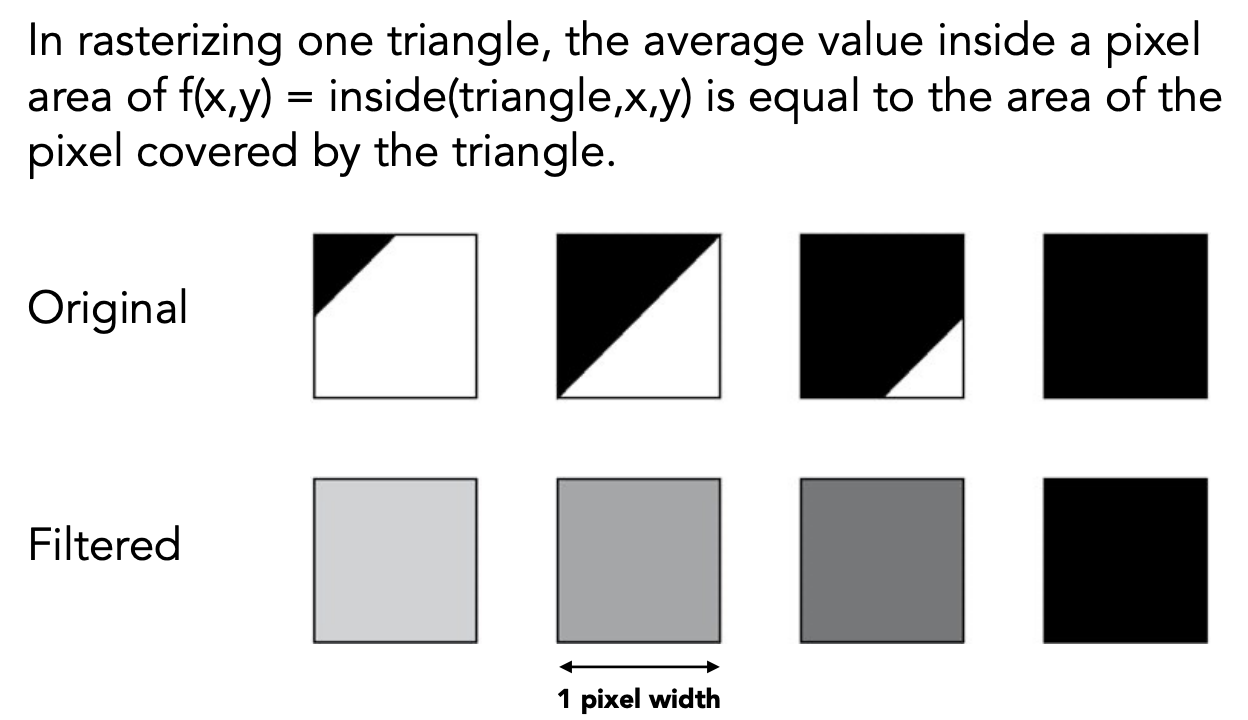
用一个1像素的方块对三角形函数做一个卷积操作:

对三角形覆盖面积求平均:
怎么计算三角形的覆盖面积,近似求解,把像素划分成很多小像素,判断小像素是不是在三角形里面再求平均:
Antialiasing By Supersampling (MSAA)
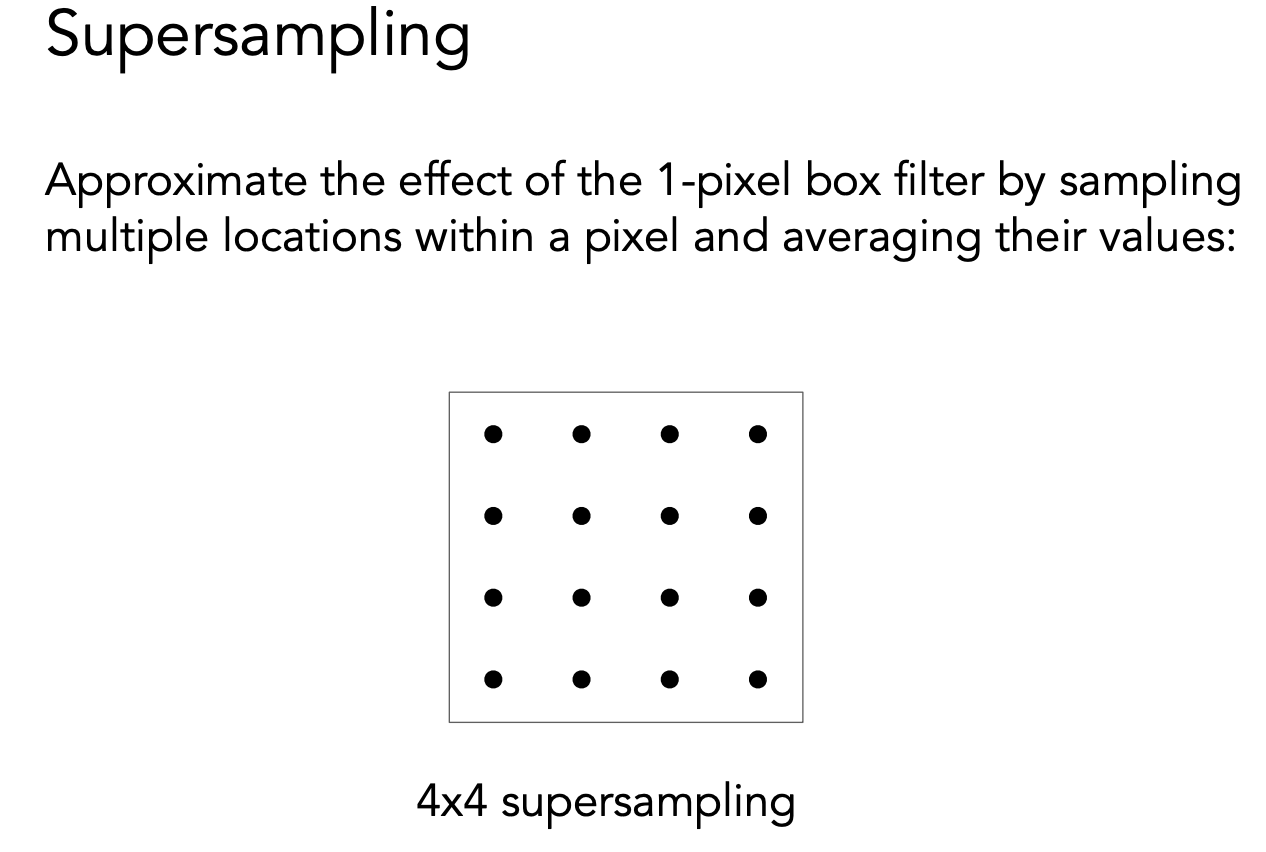
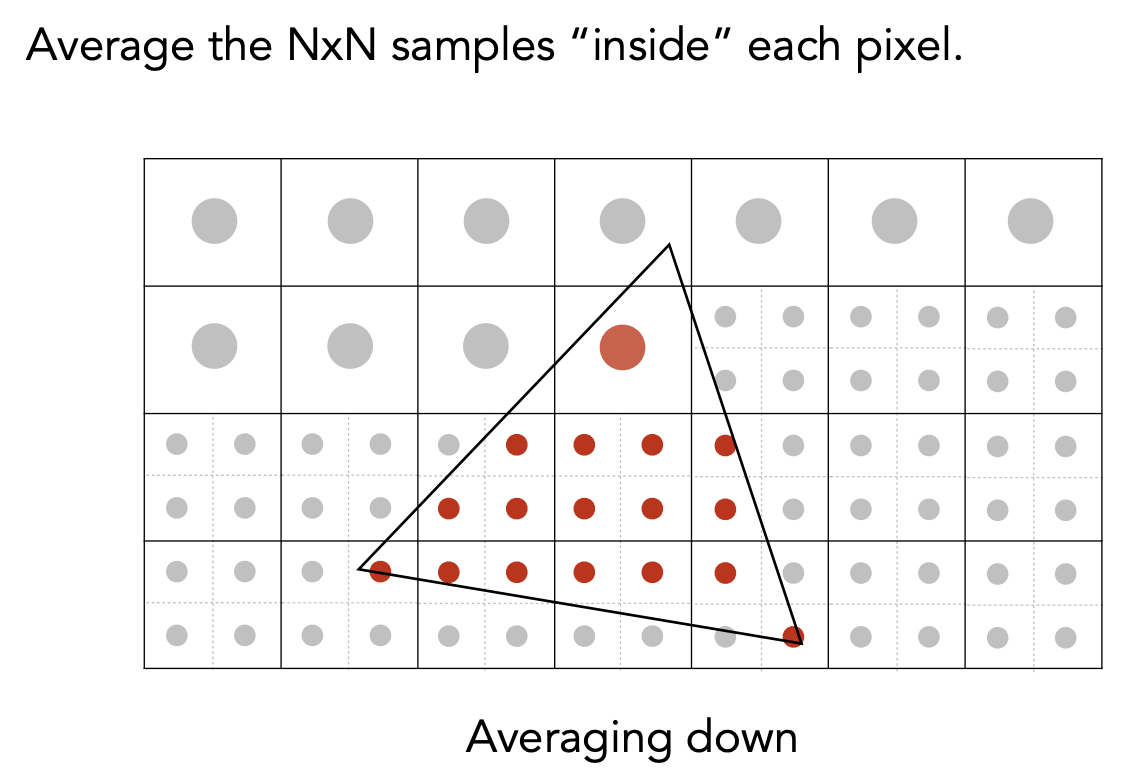
接着对格子中间进行采样(采样的结果就是平均的结果)
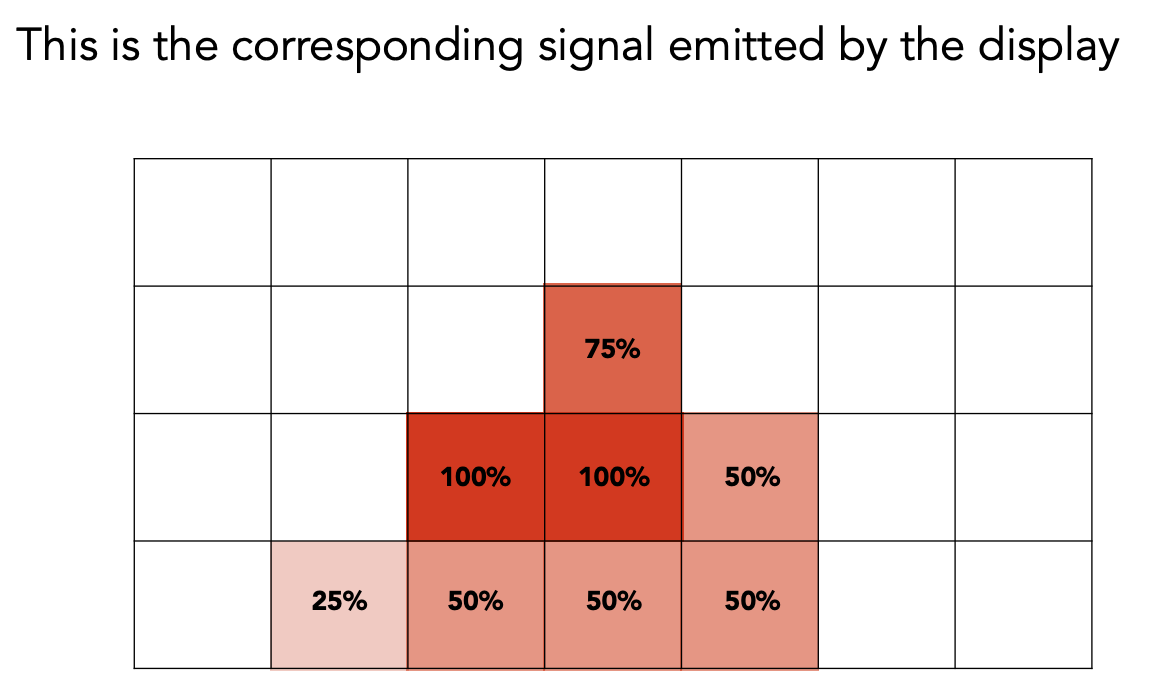
MSAA不是靠提升分辨率直接解决走样问题,增加采样点只是得到三角形的近似覆盖,屏幕像素值不变,它解决的是模糊的问题。
MSAA的代价:
增大了计算量。工业上用更有效的不规则图案来减少采样点,有一些点还会被临近的像素来复用。
其他抗锯齿:
FXAA(Fast Approximate AA 快速近似抗锯齿):和采样无关,通过图像后期处理,先得到一个有锯齿的图,再通过图像匹配的方法找到这些边界,再把有锯齿的地方换成没有锯齿的边界。
TAA(Temporal AA):静态物体两帧不变,因此相邻两帧可以用一个像素内的不同点感知是否在三角形内部,当前帧可以复用上一帧的结果。
超分辨率:
小图拉大;有一个高分辨率的图,但是采样率不够,想要把这个图恢复出来。
DLSS(Deep Learning Super Sampling)深度学习
