第五章:光栅化
光栅化(三角形)
上节课提到了观测变换:包含视图变换和投影变换。当完成观测矩阵变换后,下一步需要怎么绘制到屏幕上?这就是光栅化
上节课提到透视投影转换为正交投影,近平面和远平面 z 轴位置不变,远平面大小变成和近平面一样大。
正交投影里:x 轴定义左(l)和右(r),y 轴定义上(t)和下(b),z 轴定义远(f)和近(n)。
锥体定义
n 和 f 在正交投影和透视投影里面都是一样的,我们认为是已知的。做正交投影时我们把锥体 frustum 变成一个长方体,那么怎么定义这个 frustum?
假设我们从相机出发,看向一个区域,首先我们给这个近的平面可以定义一个出一个高度和宽度(高宽比),再定义一个视角(field of view,表示可以看到的角度范围)
下图中平面的上下两条边中点到相机的连线(红线)所夹的角度是竖直方向的可视角度,这个角度用于定义看到的世界。比如广角相机这个角度就比较大,角度越小透视投影就越不明显,比如可以拍到很远的物体。
同理可推出水平可视角度:相机和左右两条变中点连线所夹的角度。
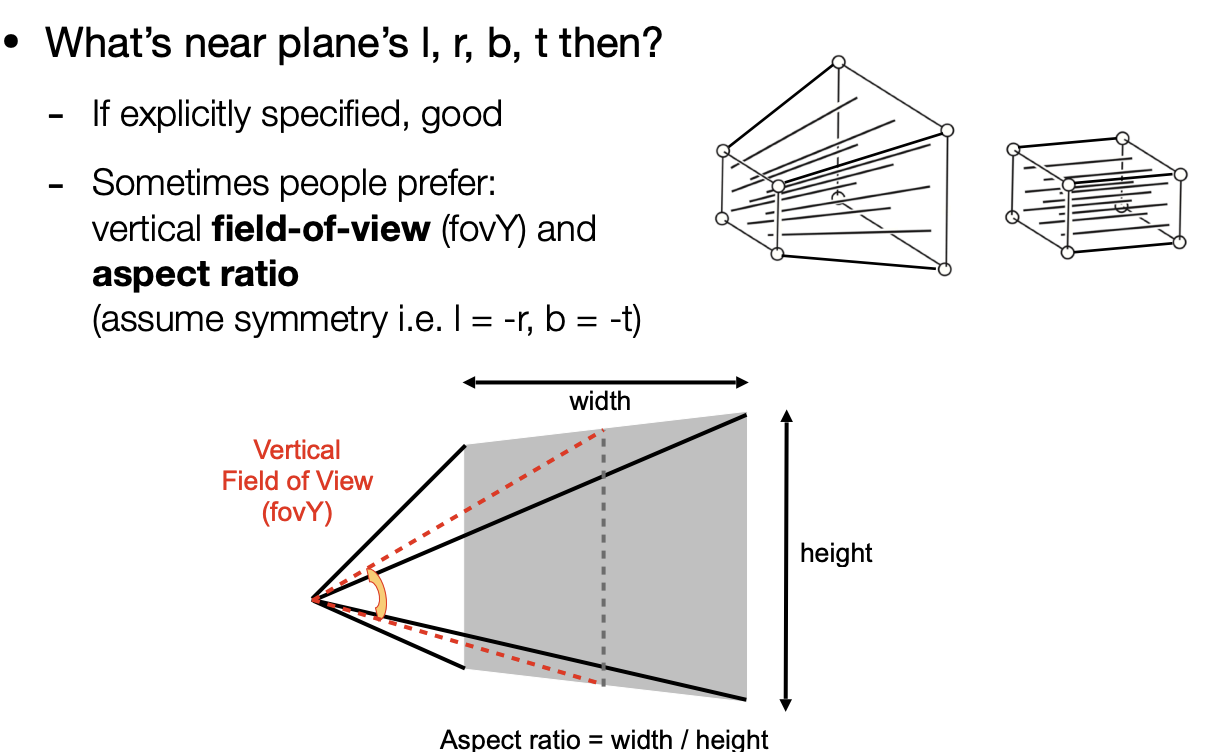
长宽比和垂直可视角可以和做正交投影的长方体转为同一个概念。
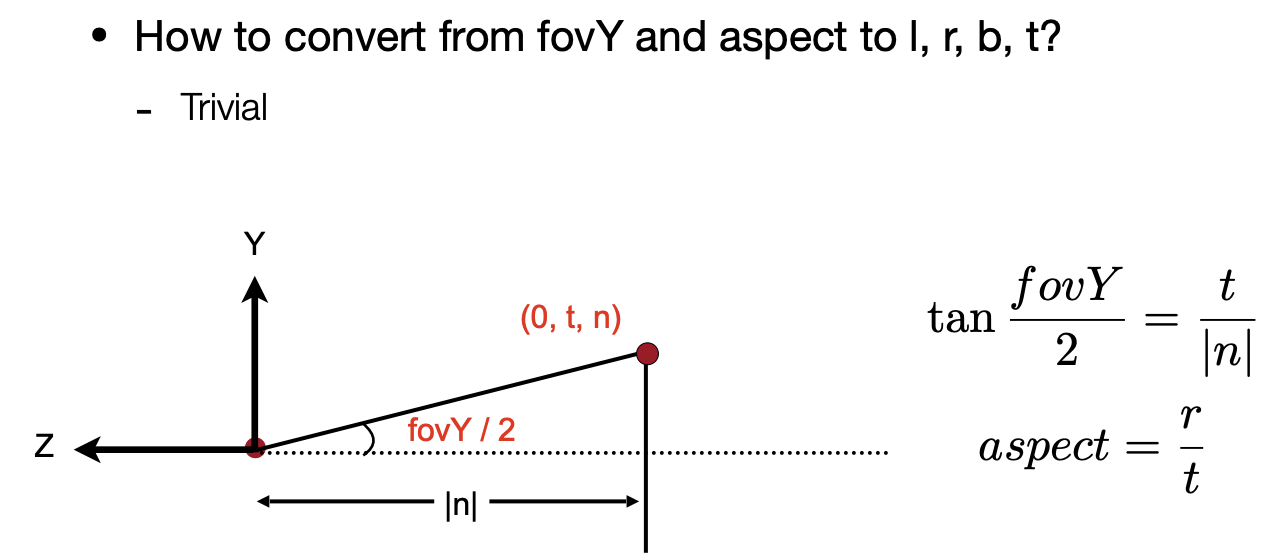
经过 MVP 投影后,我们会得到一个(-1,1)的三次方的立方形,接着我们要将它绘制到屏幕上。
屏幕是什么
1.是一个二维数组,数组的每一个元素是一个像素(pixel)
2.屏幕分辨率表示像素的多少
3.屏幕是一个典型的光栅成像设备
光栅(Raster)是德语里的屏幕的意思,光栅化即把东西画到屏幕上的过程。
pixel 表示 picture element
这门课里,我们把像素认为是一个个的小方块(实际的像素比这复杂得多),每一个方块表示一个颜色,一个像素里的颜色都不会变化。一般像素的颜色可以划分为不同的等级(0-255),用 RGB 表示。
屏幕的空间
认为屏幕左下角是原点,向右是 x,向上是 y。像素的坐标都是写成 x,y 的形式,用整数坐标来表示。如果一个屏幕的分别率是 width*height,那么所有的像素可以用(0, 0)到(width-1,height-1)来表示,所有像素的中心在(x+0.5, y+0.5)上,屏幕覆盖的范围为(0, 0)到(width, height)。
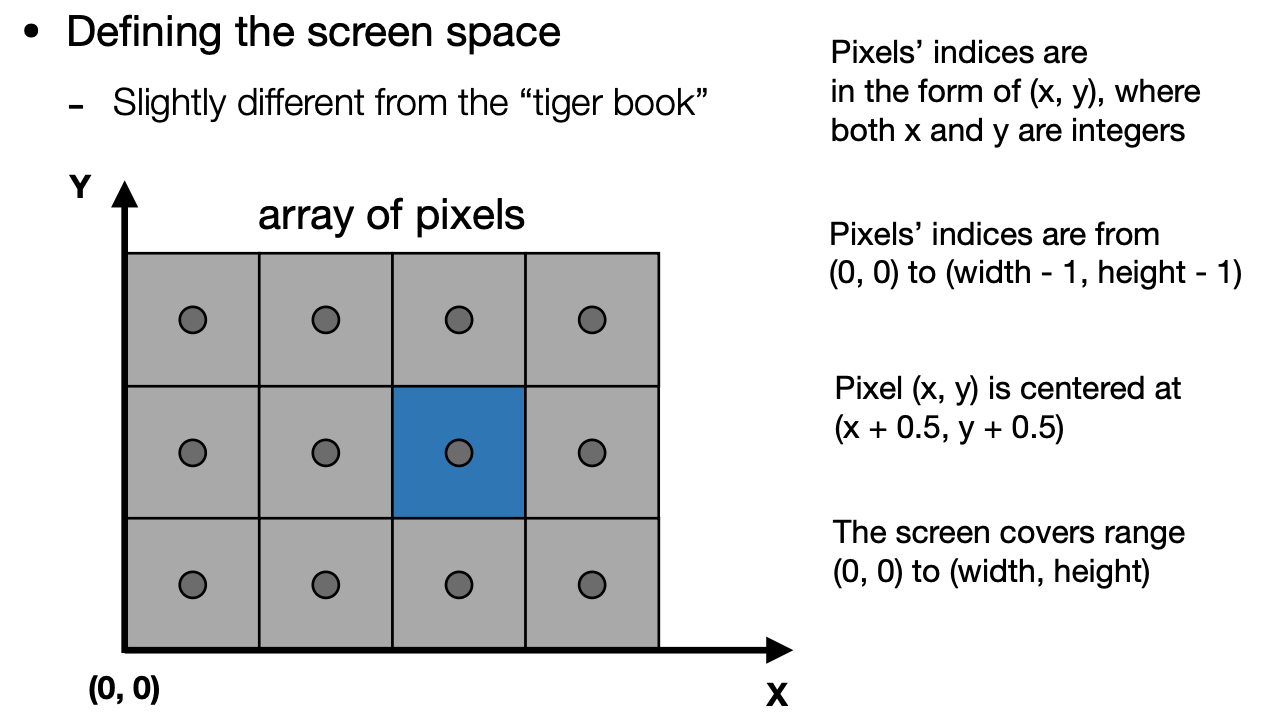
接下来需要把[-1,1]³ 映射到屏幕上,先不管 z 轴,[-1,1]² 转换为[0,width]和[0,height]。
先做缩放,然后要保持原点不变,所以还要做一个平移。这个变换被称为视口变换。
接下来要把所有的结果打散成像素,画到屏幕上。
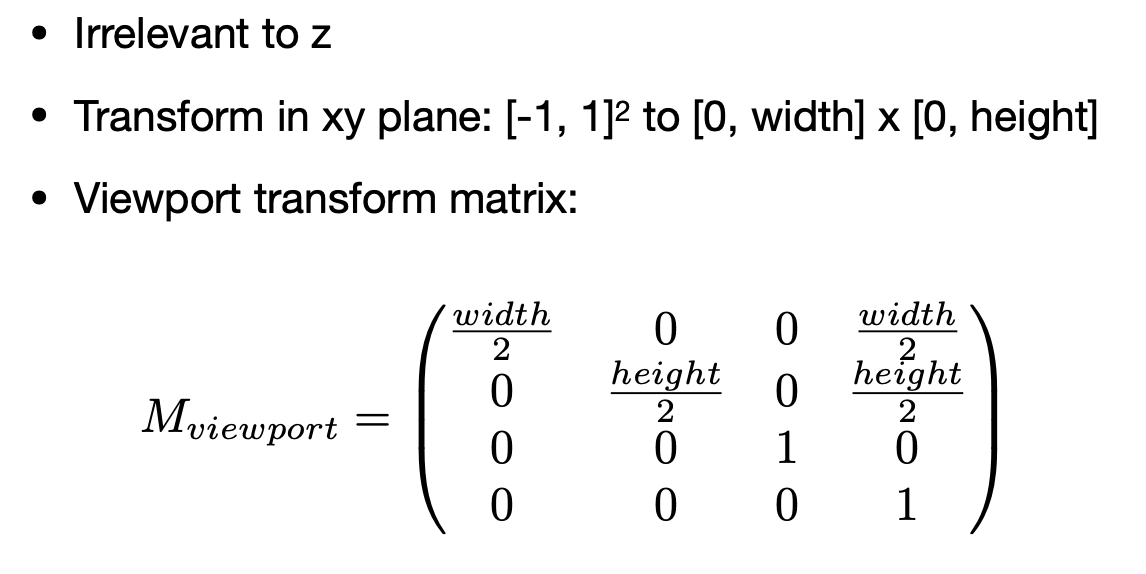
成像设备
早期的 CRT(Cathode Ray Tube)显示设备:
成像原理:阴极射线管,电子加速后穿过显示设备,然后做偏转,电子打到屏幕上成像。
成像的过程就是,通过扫描的方式,在屏幕上一行行的画线。提高扫描的速度:隔行扫描
现在的显示设备:
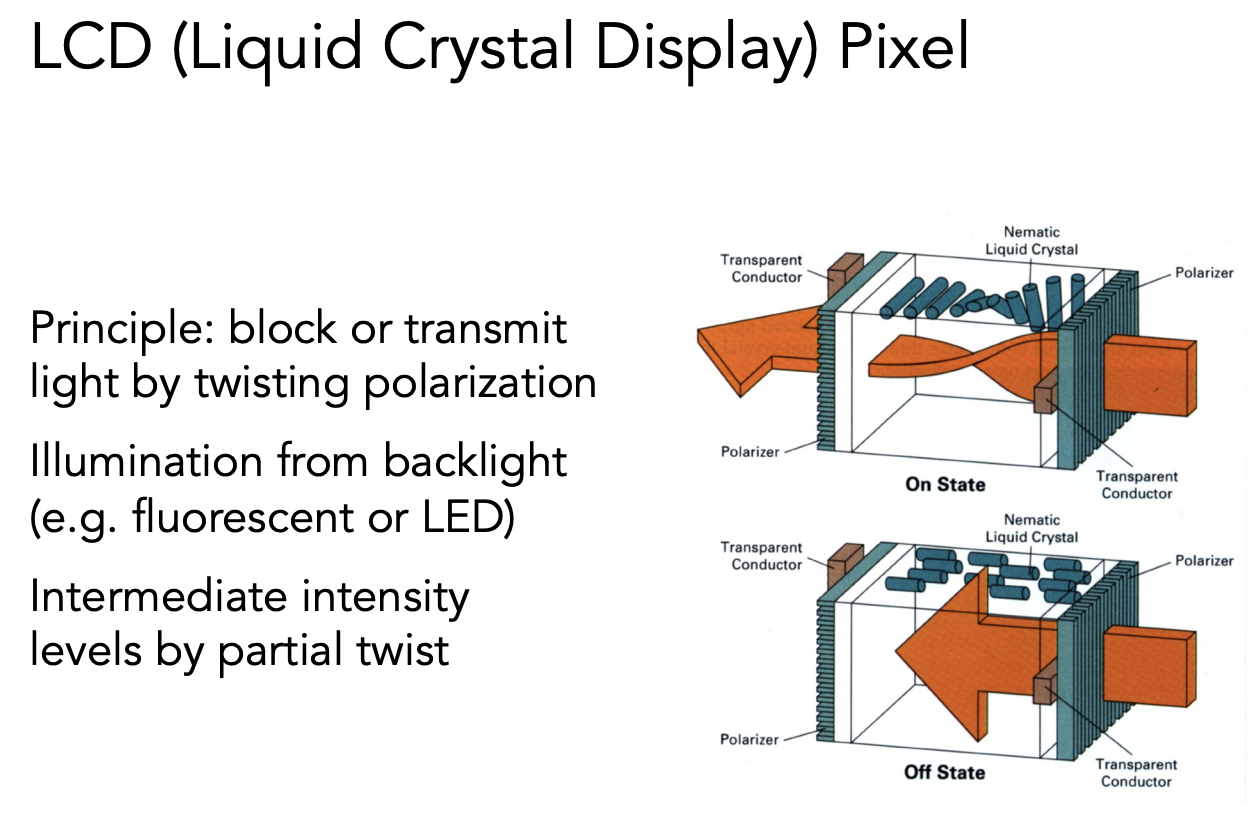
LCD(Liquid Crystal Display)显示设置
把内存(比如显存)中的一块区域映射到屏幕上。
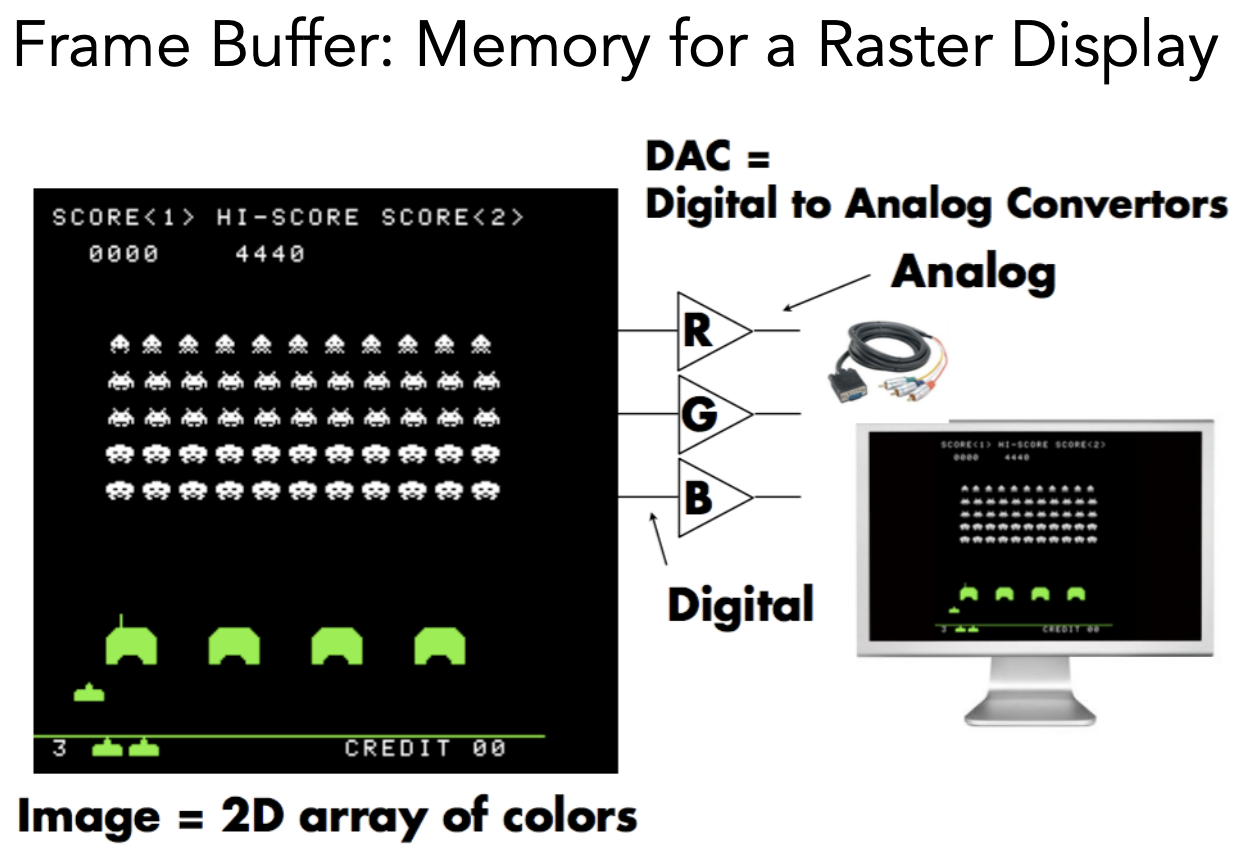
液晶会通过自己的不同排布影响光的偏振方向
LED 显示设备(发光二极管)
墨水屏(电压使得黑白墨水翻转, 刷新率很低)
怎么在成像设备上绘制
成像即把变换后得到的多边形的顶点打散到各个像素上
三角形
- 三角形是最基础的多边形,任何多边形都可以拆成三角形
- 三角形内部一定是平面的
- 三角形内外定义一定是清晰的
- 只要定义三角形的三个顶点,就可以做到一个顶点属性到另一个顶点属性的插值
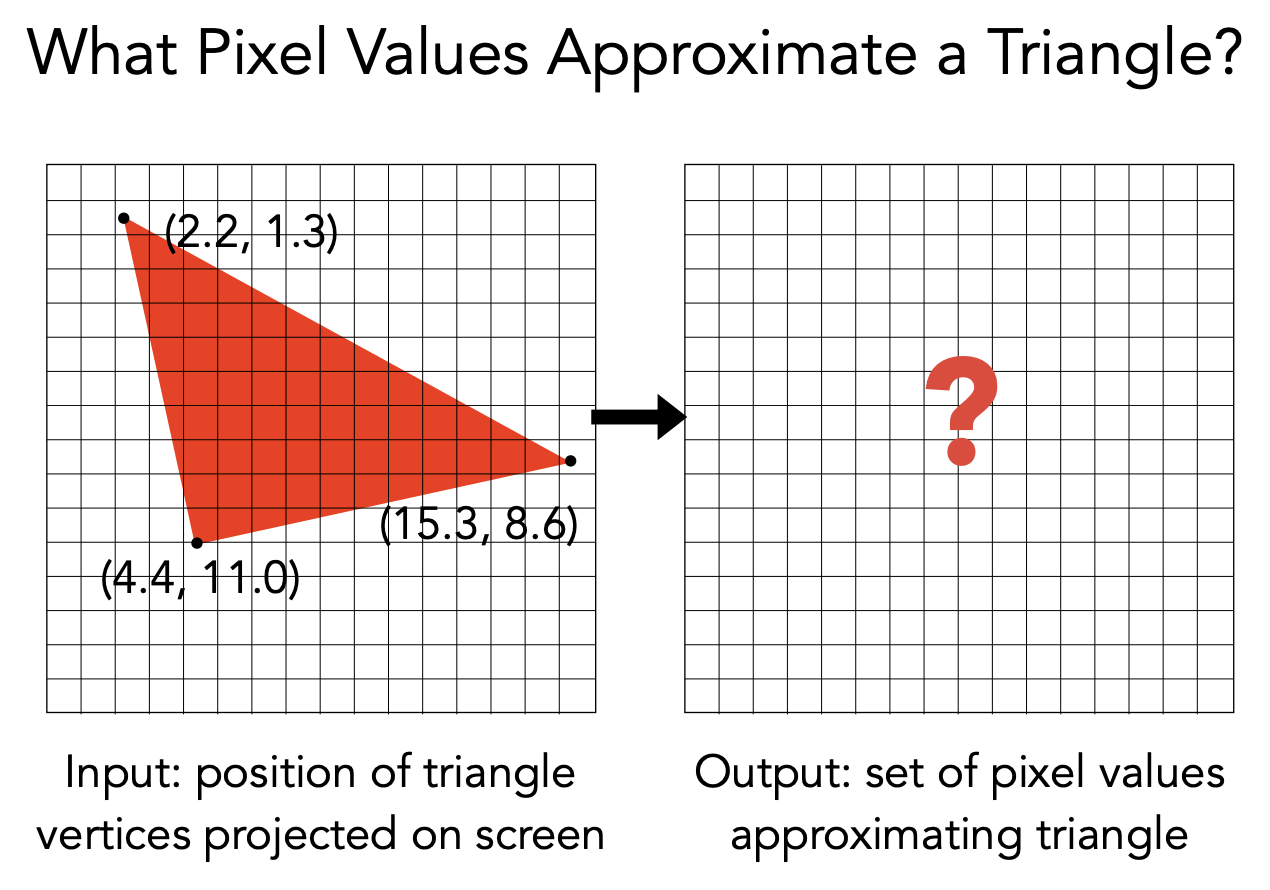
当三角形的边只有一部分覆盖到像素,怎么判断是不是要绘制,即判断像素中心点和三角形的关系?
采样
把一个函数离散化的过程(给不同的 x 计算不同的函数值)
用像素中心进行采样,定义不同的函数在像素中心的值

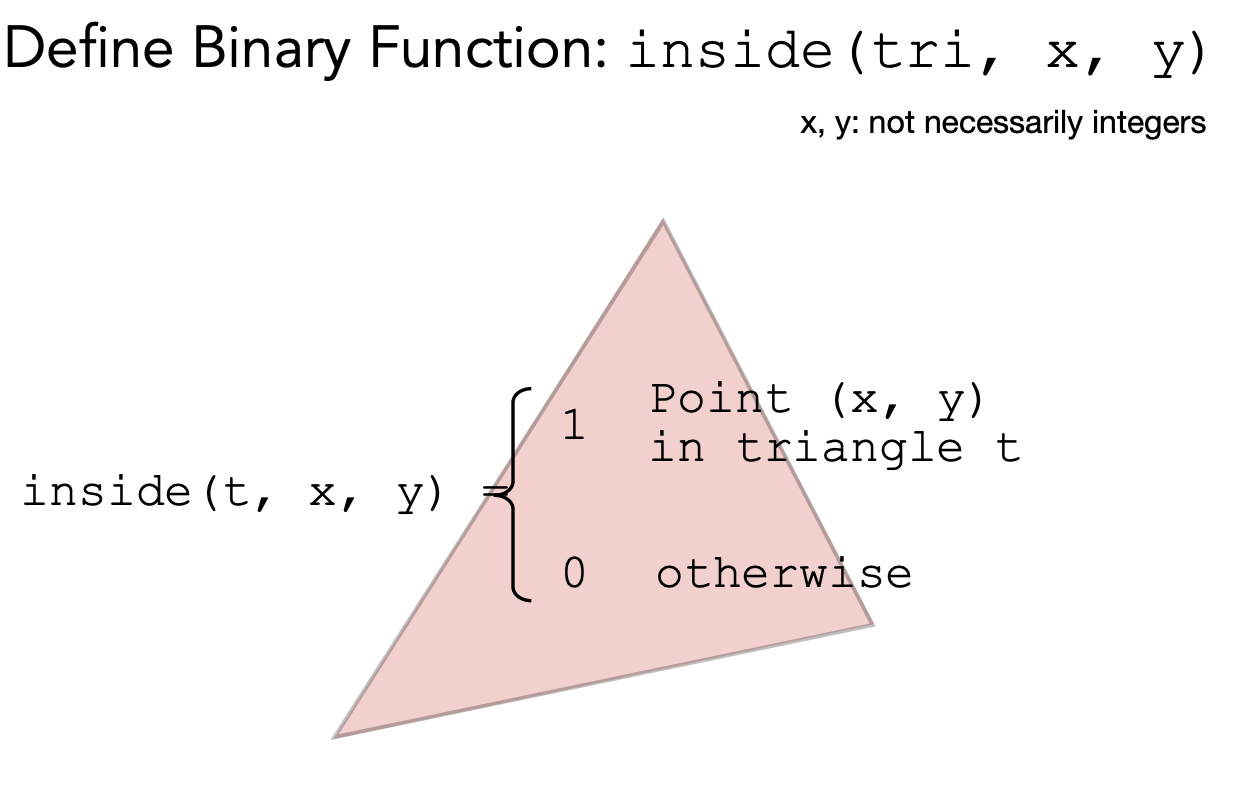
定义一个 inside 的含义,给定任意(x,y)坐标,判定它是否在在三角形内,在三角形里其值为 1,不在则值为 0。

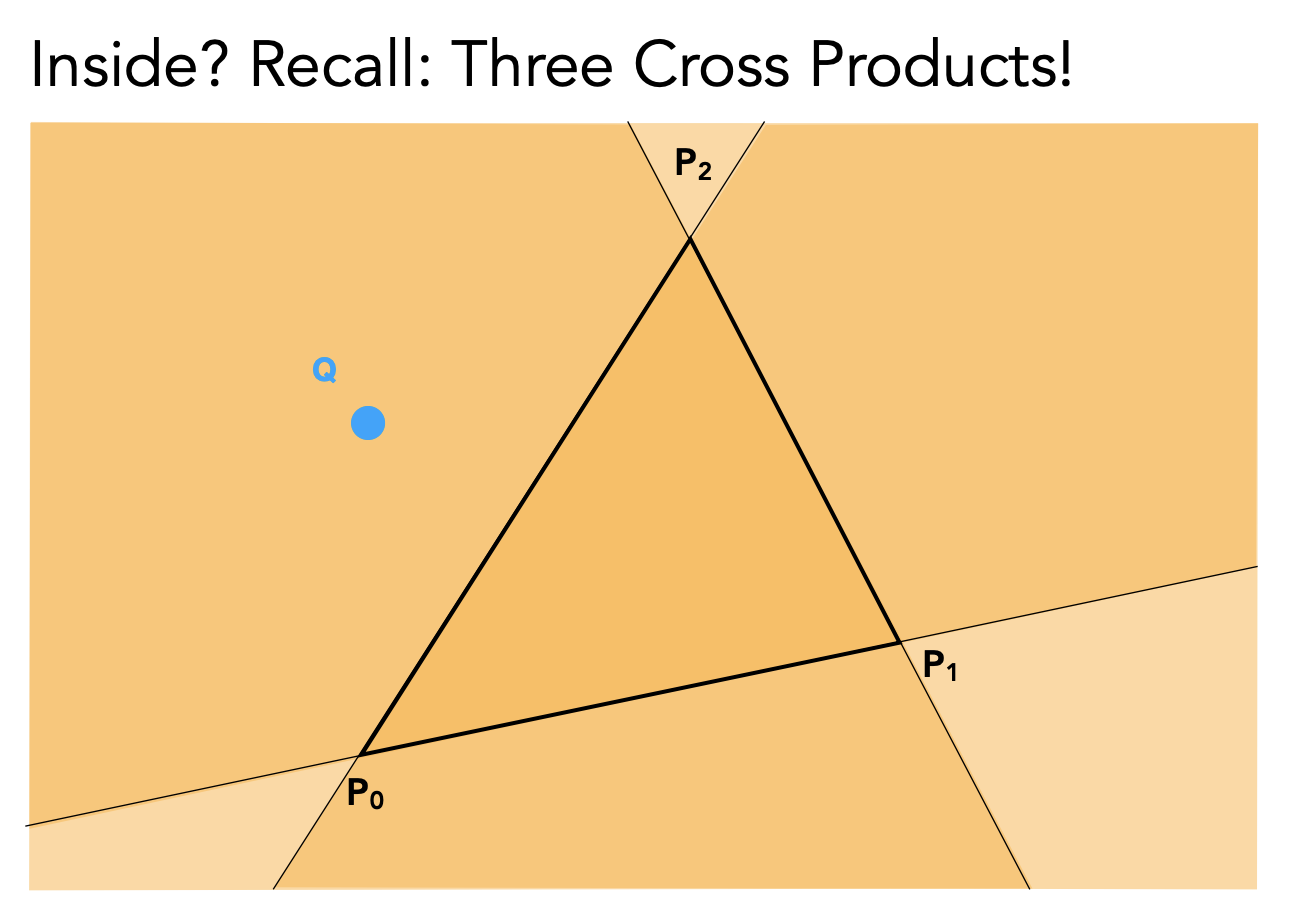
通过叉积的计算可以判断一个点是否在三角形内部
如果有一个点正好在三角形的边界上,自己定义一个标准,不同的 API 可能有不同的标准。
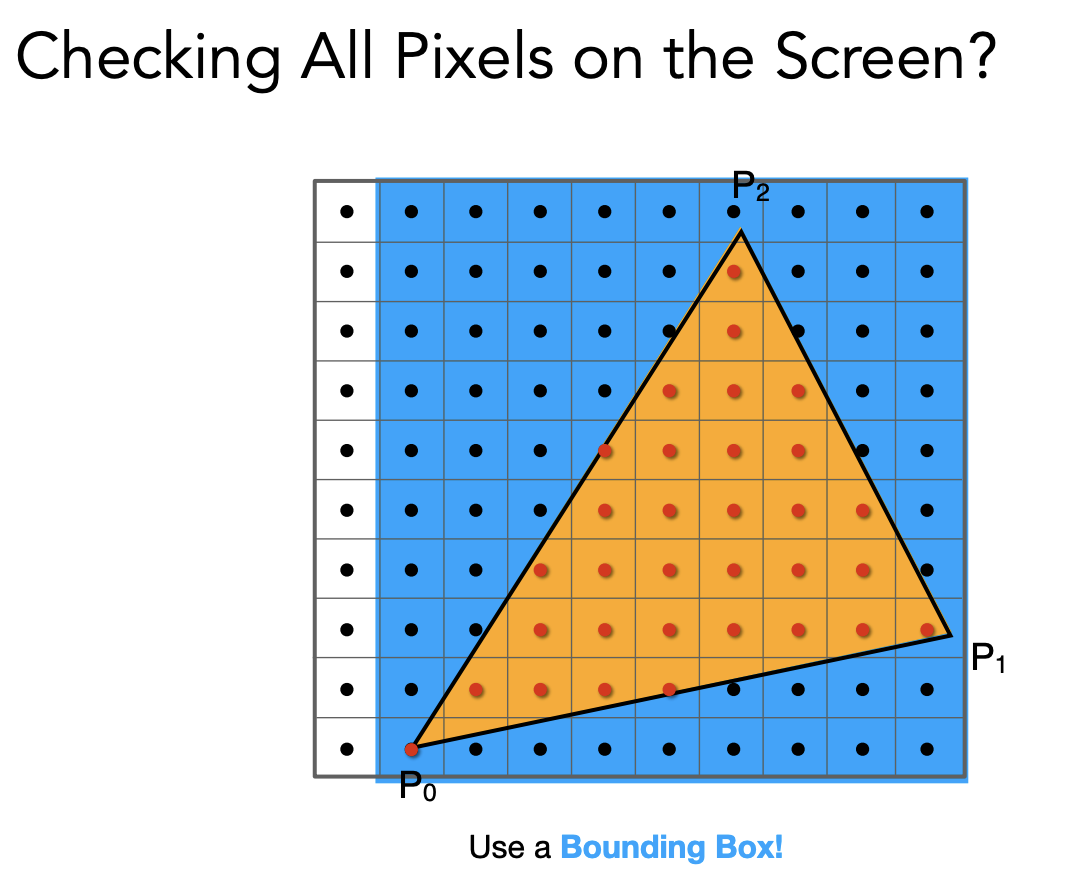
不需要对屏幕上的所有像素做光栅化,只需要找到三角形的包围盒。
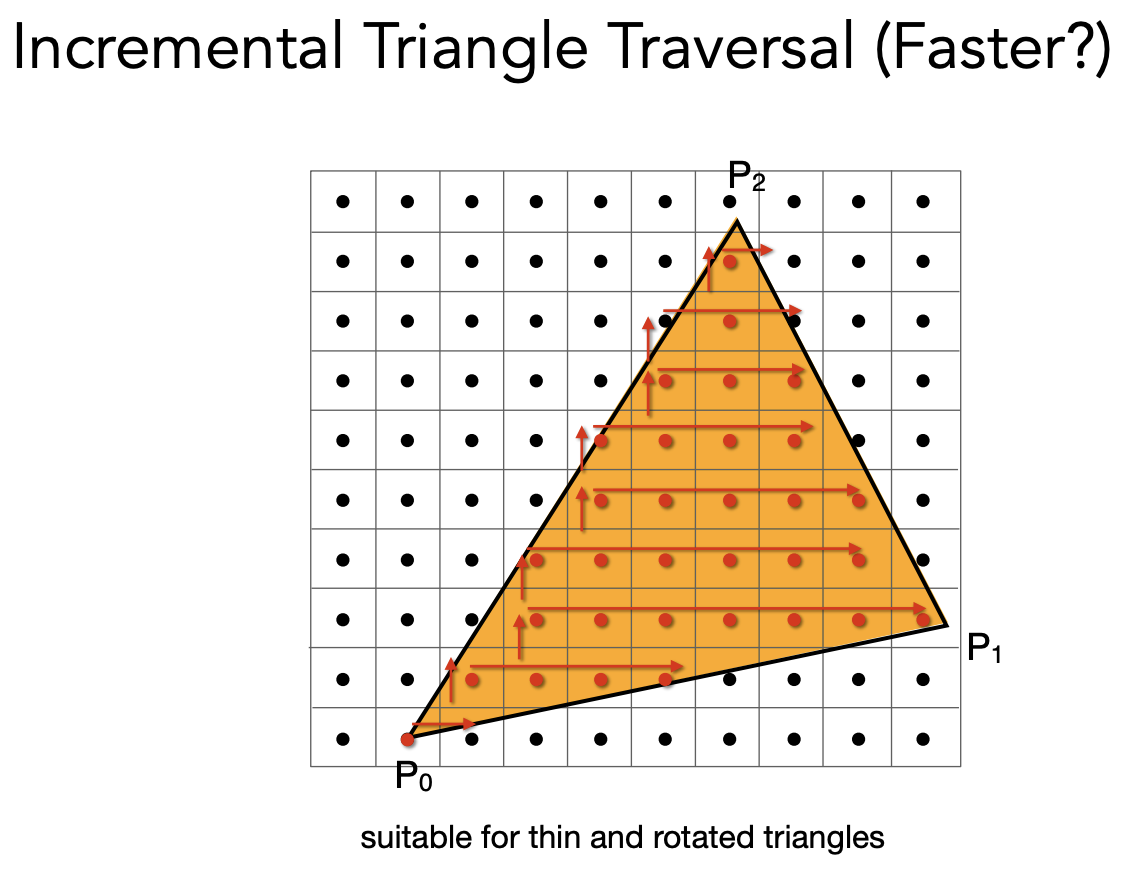
更快的方式是只找每一行的最左和最右。
实际的像素
bayer pattern(右侧的)绿色出现的频率最高,因为人眼对绿色更敏感

打印和屏幕相反,打印是一个减色系统(因为颜色越多越黑),但是屏幕 rgb 值越高,越亮,越靠近白色

光栅化后,由于颜色均匀的填在像素格子里,就会形成锯齿,采样率不够高会导致锯齿更明显,造成走样问题。