第二十二章：动画和仿真

发表于 2023-08-17 阅读次数：本文字数： 2.7k 阅读时长 ≈ 10 分钟

动画和仿真

上节课主要说到了模拟各种运动的各种知识，比如定义一个物体的速度、加速度，就自然能算出来物体在某个时刻出现在某个位置。

这节课从上节课的概念出发，说一下具体的解法，怎么计算物体在不同时间出现的位置。

本节课的主要内容：

单粒子模拟

刚体模拟

流体模拟

模拟物体的运动即规定一个物体在任何时刻的速度，同时知道开始出现的位置，就求解在某个时间后物体出现在哪里。

如果是匀速的，在 t0 时刻出现在某个位置，在 t1 时刻出现的位置即为 t0 的位置加上速度乘时间。

但大多数时候没有这么简单，比如要模拟一个粒子在速度场中的运动。

速度场和光场、磁场类似，表示空间中速度的分布。任意一个粒子的运动可以由一个速度场决定，该速度场是位置和时间的函数。

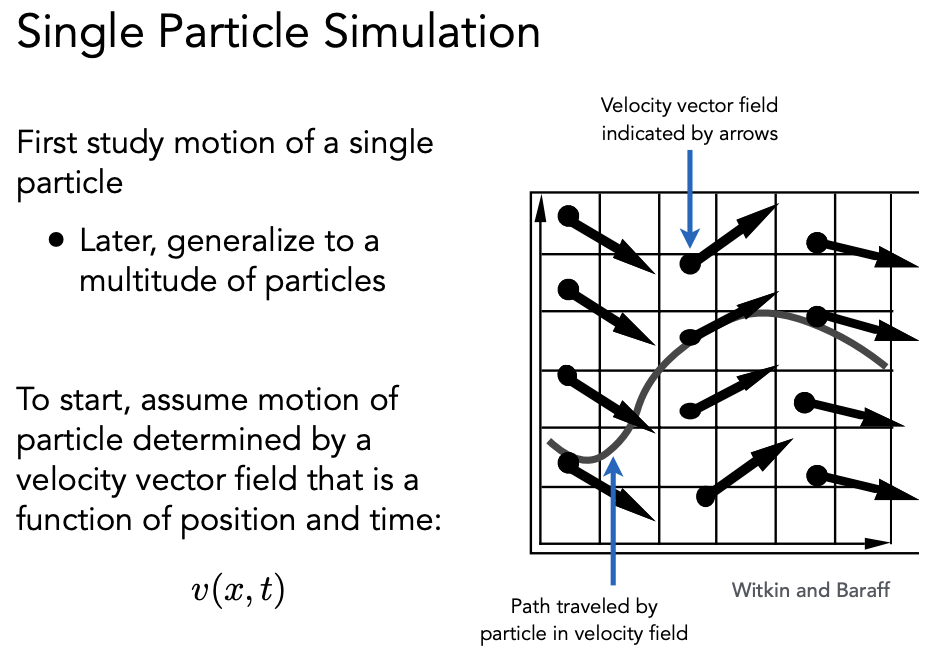
先从简单的出发，研究一个粒子的运动，后面再提高到很多粒子去考虑。

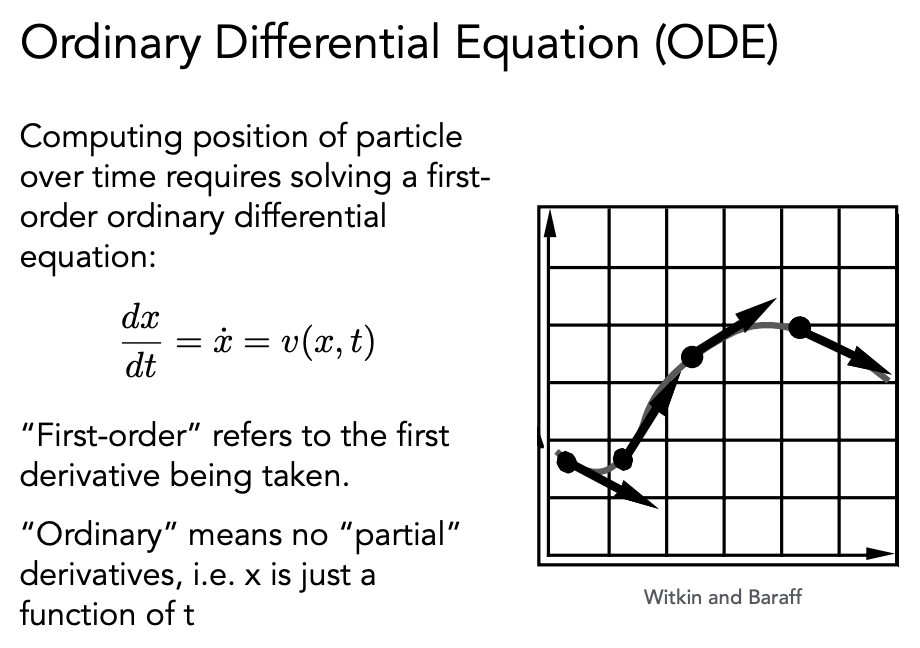
求解一个例子的速度即求解一个一阶常微分方程：

一阶表示知道一个量的微分是多少，希望推出这个量是多少

常微分方程表示不存在对其他变量的微分（对应于偏微分可能存在对多个变量的微分）

求解这个常微分方程，给定粒子的初始位置 x₀，用积分求解这个粒子在时间 t 的位置，得到粒子的运动轨迹。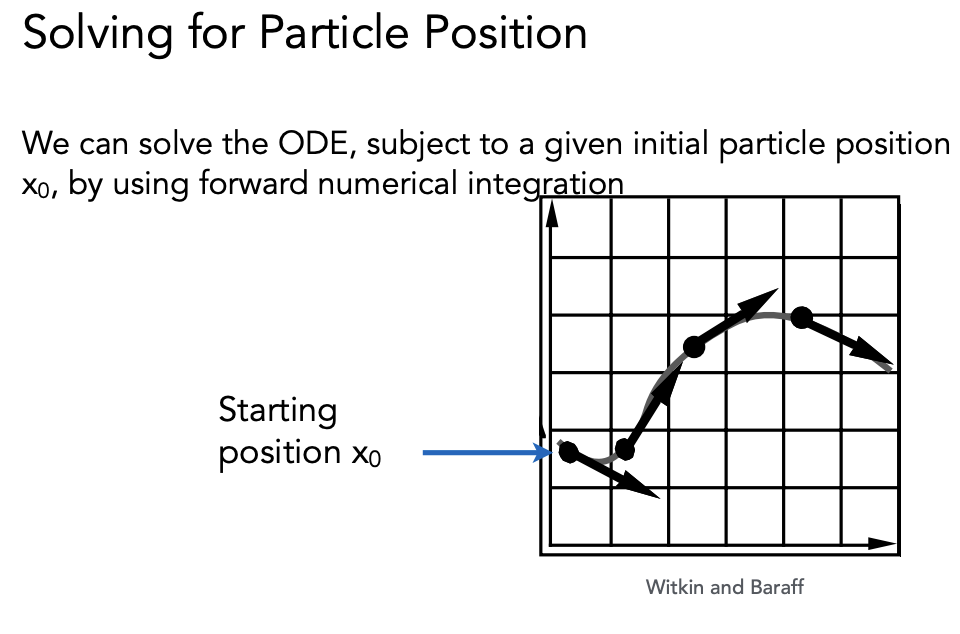

怎么求解？可以把时间细分成很多小块，计算每个小块（比如时间 t+ 步长 Δt）粒子的位置的变化，在时间上做离散。

下一帧的位置是上一帧的位置加 Δt 乘速度，下一帧的速度是上一帧的速度加 Δt 乘加速度

始终都是用上一时刻的量计算下一时刻的量（也可以用计算出来的下一时刻的量计算下一时刻的量，比如用计算出来的下一时刻的速度来计算下一时刻的位置，但这种方法就不是欧拉方法）

欧拉方法的问题：
不准确，且稳定性上会出问题，迅速地变得不稳定。

对于不准确的问题：步长分的越细，就模拟得越精确。

对于稳定性的问题：

如果速度场是螺旋形的，任何时刻都有一个和位置方向垂直的速度，物体应该是按照圆周运动来运动的。但用欧拉方法无论取多大的步长，无论如何得到的线都不可能沿着这个螺旋形走，最后都会飞出去。

如果是下面这幅图的情况下，正常的运动是从左到右走到中间那条线上，但是欧拉方法 Δt 的会让运动轨迹上下震荡走越偏越远。

这种情况在信号处理上被称为正反馈，即一旦出现问题，这个问题会被无限放大。

误差和不稳定性

一些用数值微分方法解决的问题都会遇到这些问题：

误差
- 每一步计算都会有误差，最后累加起来会变成更大的误差。但是可以通过用更小的步长降低误差
- 误差在图形学应用中影响大，因为主要关注看起来效果怎么样，不要求物理上的完全一致
不稳定
- 有任何一个模拟方法，不管怎么去模拟最后得到的结果都会和正确的结果差的很远，且越来越发散
- 不稳定是模拟中一种不能被忽视的非常基础的问题

中点法

假设有一个点用欧拉方法模拟经过 Δt 从原始点到 a 点，取原始点到 a 点的中点 b 点，再回到原始点，应用 b 点的速度重新算一遍欧拉方法，达到 c 点，这样计算出来的结果就会比欧拉方法更准确。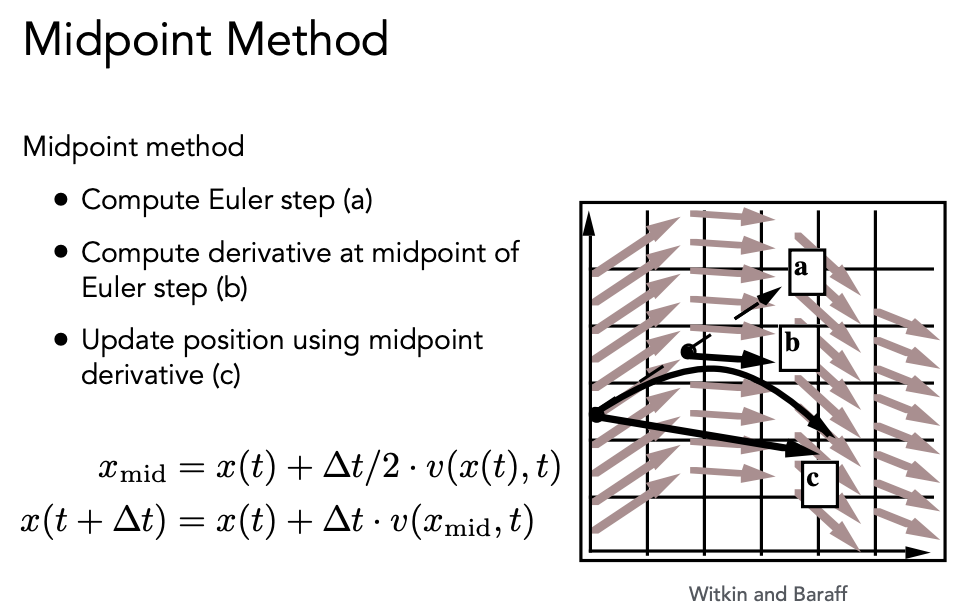

中点法之所以更准确，是因为中点法比欧拉方法多出了一个二次项，得到了一个类似抛物线的运动轨迹。原本欧拉方法是一个局部线性的估计模型，中点法算出了一个局部的二次模型。

Adaptive Step Size
应用两次 Δt/2 和应用一次 Δt 的结果进行比较，如果应用两次 Δt/2 计算的结果更准确，则把时间拆分得更短一点。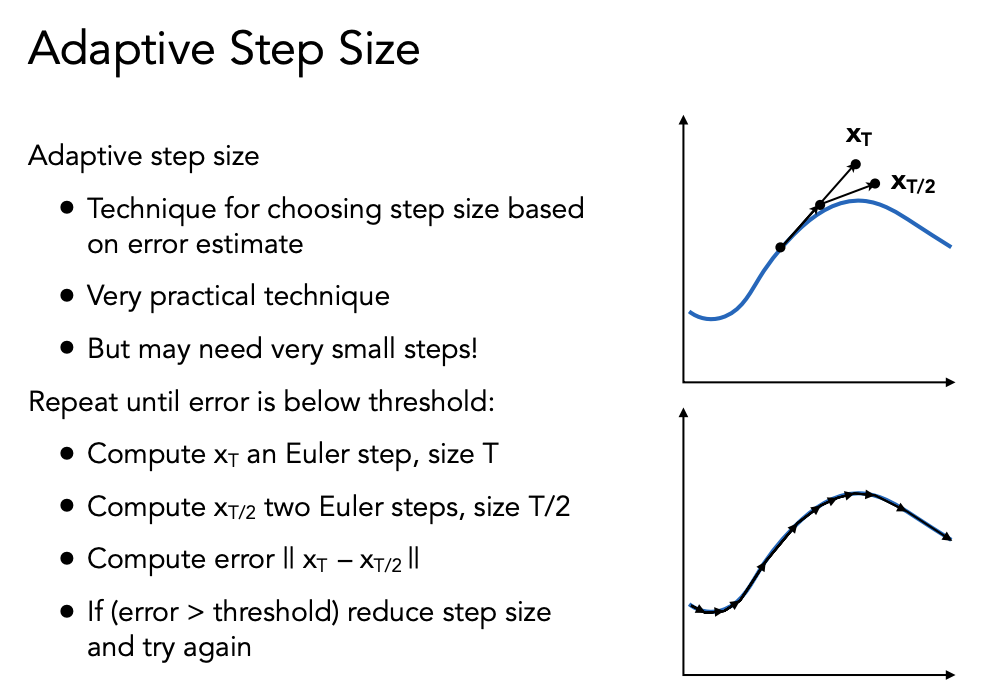

隐式欧拉方法

怎么定义一个方法是不是稳定的

用局部截断误差（每一步会产生的误差）和最后累积起来误差来衡量稳定性
研究这两个数字没有意义，应该研究他们的阶。即研究这两个数字和取的 Δt 的关系，误差是如何随着更小的 Δt 减小的
隐式的欧拉方法是一阶的，即：
- 局部的误差是 O(h2)的
- 全局的误差是 O(h)的
h 表示步长（即 Δt），h 越小，误差越小。O(h)表示：
- 如果把 h 减小一半，得到的误差也会减小到一半。阶数越高越好，如果是 2 阶的，假如 h 减少一半，那误差就会减少到 1/4。