第九章：重心坐标、纹理

着色 1-2

• Blinn-Phong 反射模型（

  • 高光、漫反射、环境光，如何定义材质不同的表面和光线如何作用，可以得到不同的外观

• 着色模型/频率

  • flat shading、gouraud shading、Phong shading

• 实时渲染管线（vertax processing，fragment processing）

• 纹理映射

本节课

着色 3

• 重心坐标（插值）
• 纹理怎么贴
• 纹理的应用

重心坐标

为什么要做插值？

• 希望在属性三角形内部做一个平滑的过渡

需要插值哪些内容？

• 纹理的坐标：三角形不同的顶点可以对应纹理的一个顶点，那么三角形内部就可以对应纹理的不同坐标
• 颜色：逐顶点插值得到三角形内部的颜色
• 法线

如何在三角形内部做属性的插值？

• 引入重心坐标

什么是重心坐标

​​​​

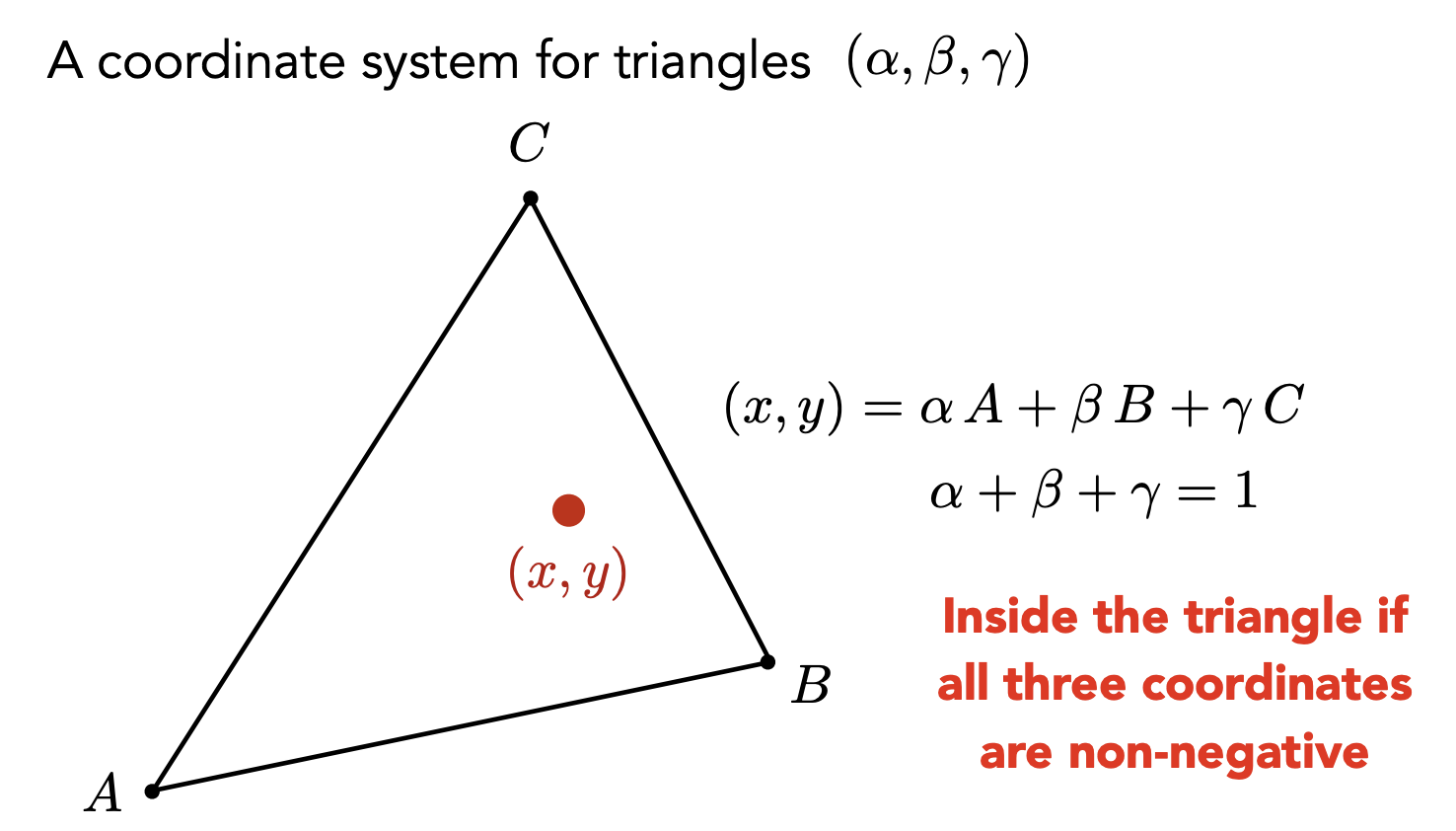
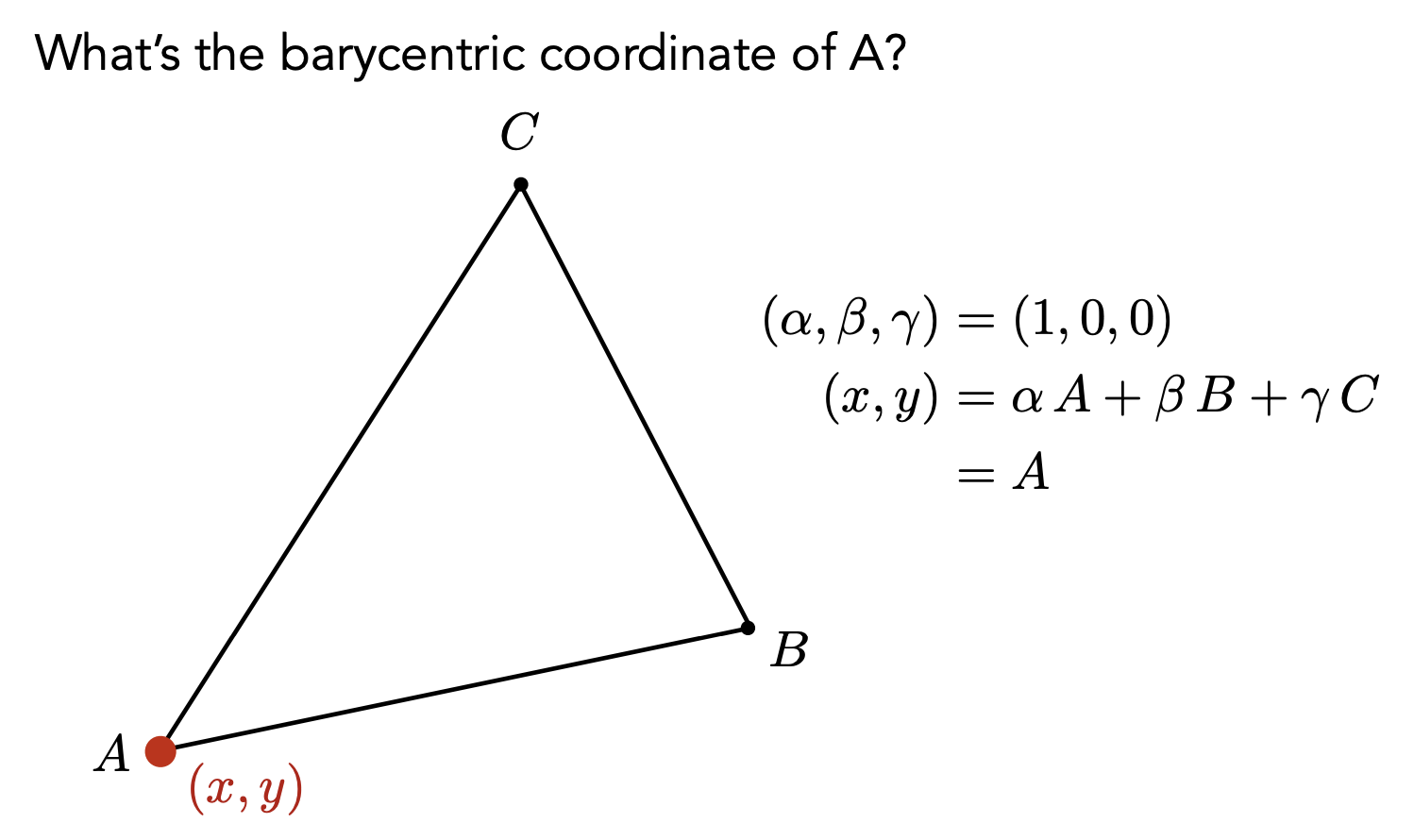
三角形平面内的任意（x,y）都可以表示为顶点的线性组合

如果这个点要在三角形内，α，β，γ 必须都为非负数

​​

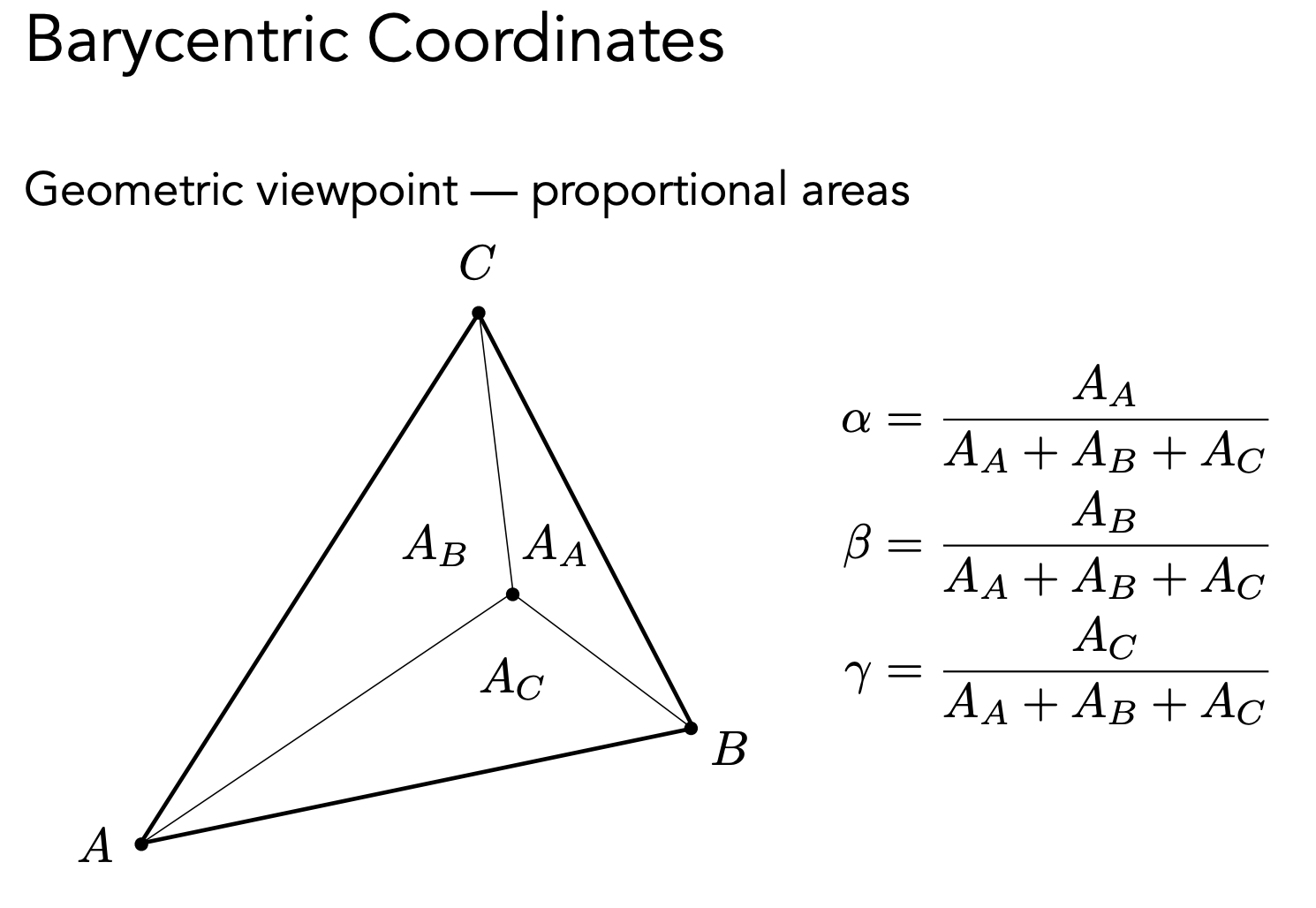
可以通过面积比计算 α，β，γ，已经一个点的坐标和三个顶点的坐标，做叉乘可以计算每个三角形对面积

​​

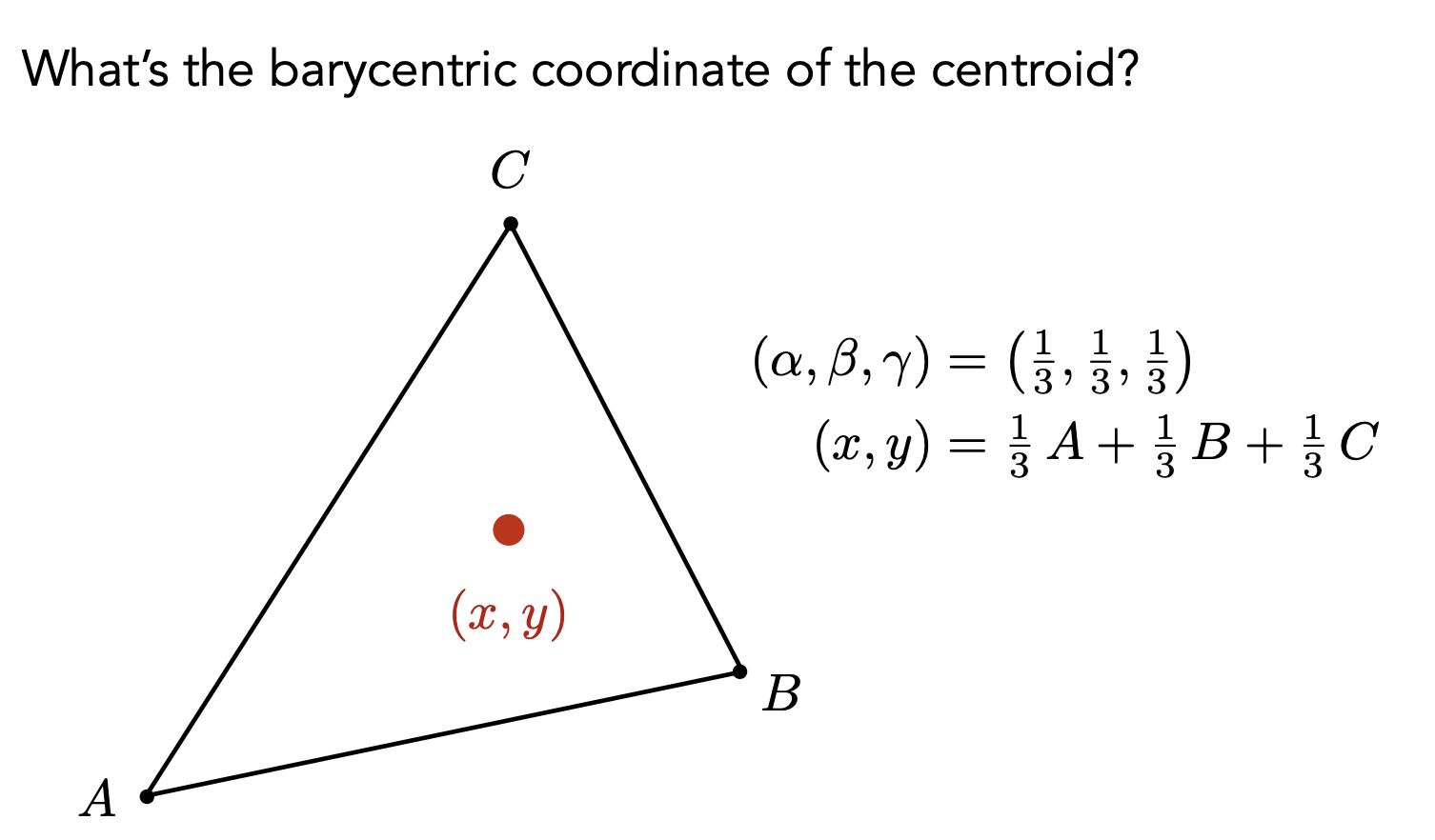
三角形的重心，把三角形等面积地分为了三部分，因此重心坐标 α，β，γ 都是 1/3。

​​

也可以用公式进行计算

​​

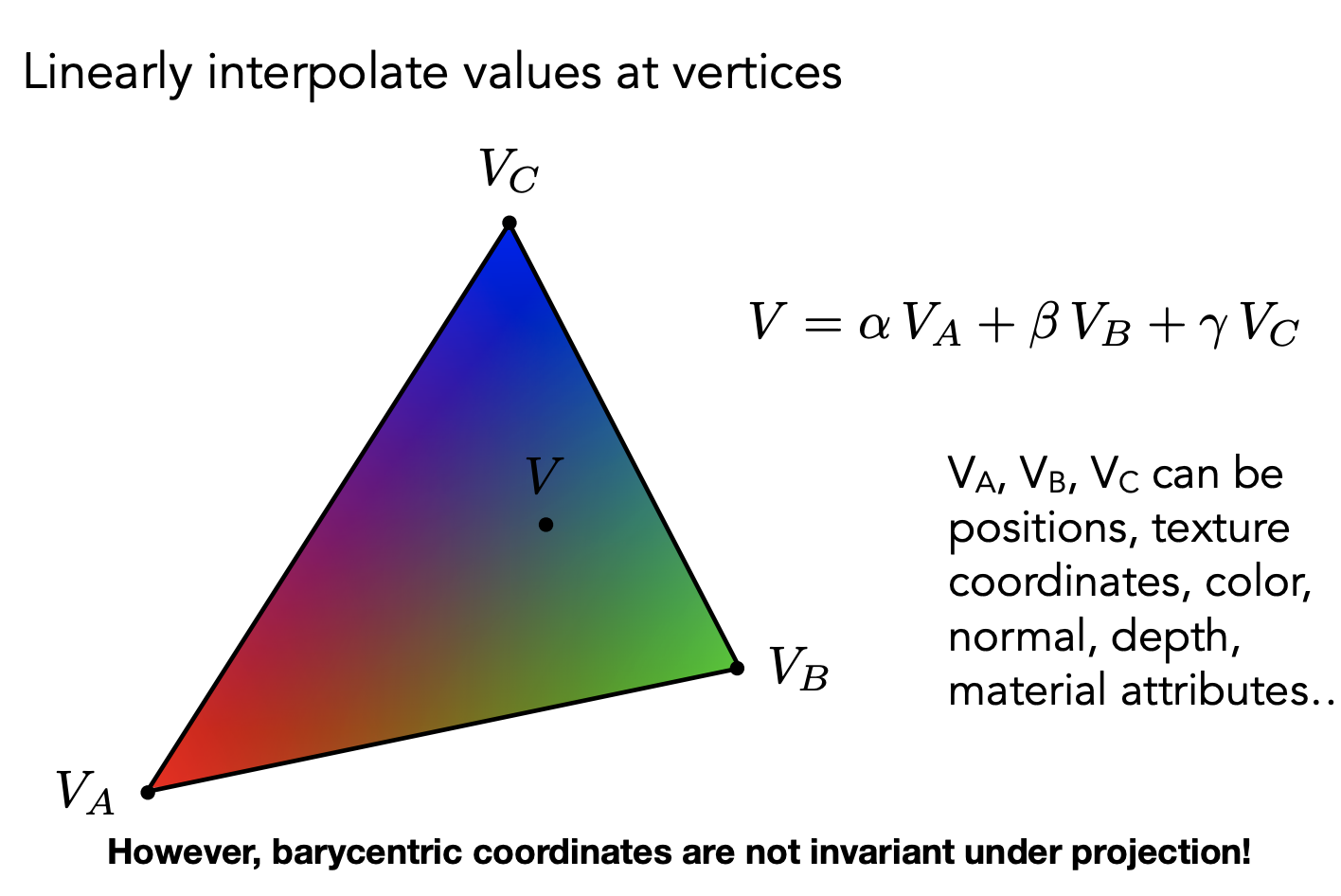
得到三角形里任意一个点的重心坐标后，就可以对属性（颜色、法线、深度）做线性插值。

重心坐标问题：在投影变换下重心坐标不能保持不变。所以做插值的时候，如果取的是三维空间中的坐标，只能在三维空间下做插值，不能投影到二维再做插值。

纹理应用

​

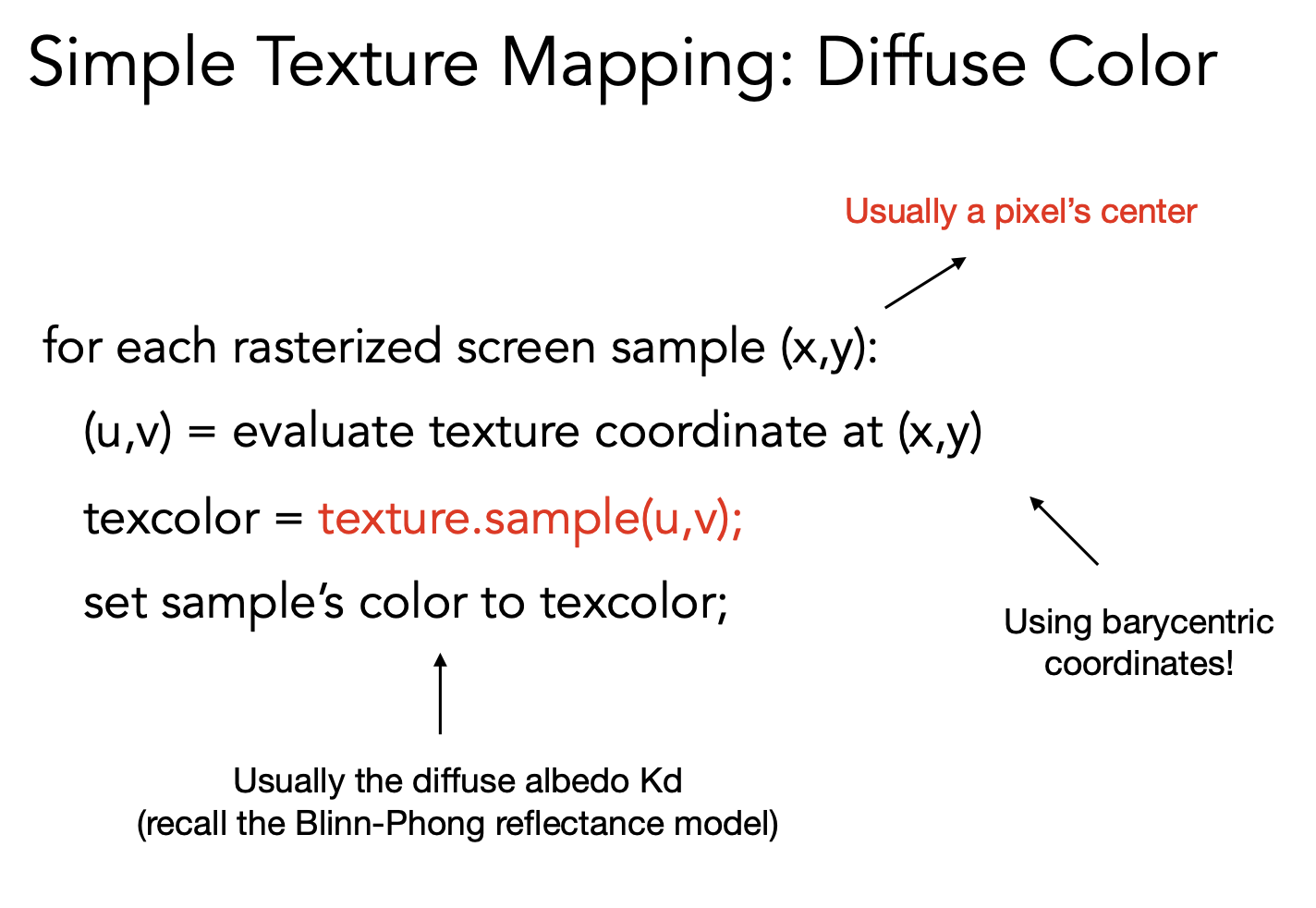
每个屏幕上的采样点坐标对应一个纹理坐标，设置采样颜色为纹理颜色。

纹理应用过程中会遇到一些问题：
纹理放大

如果纹理图片太小了

​​

Nearest：一个屏幕上的像素点对应的纹理坐标可能是小数，可以四舍五入为整数，使用用整数对应的纹理像素（texel），即多个像素可能对应同一个纹素。

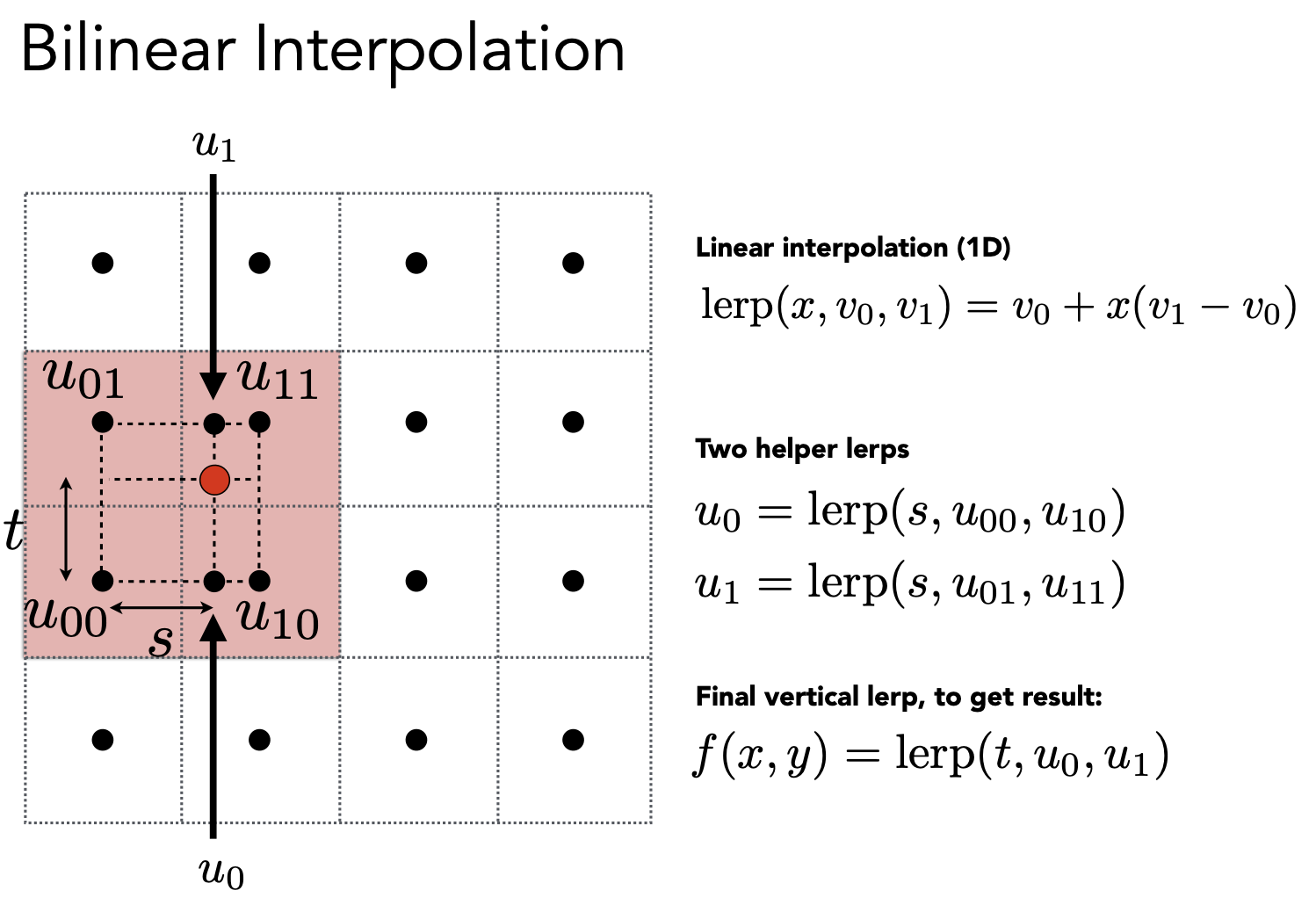
Bilinear（双线性插值）平滑过渡：

先水平方向做插值，再竖直方向做插值。（方向反过来也是一样）

​​

Bicubic 插值：取临近的 16 个点。

如果纹理图片太大了

​​

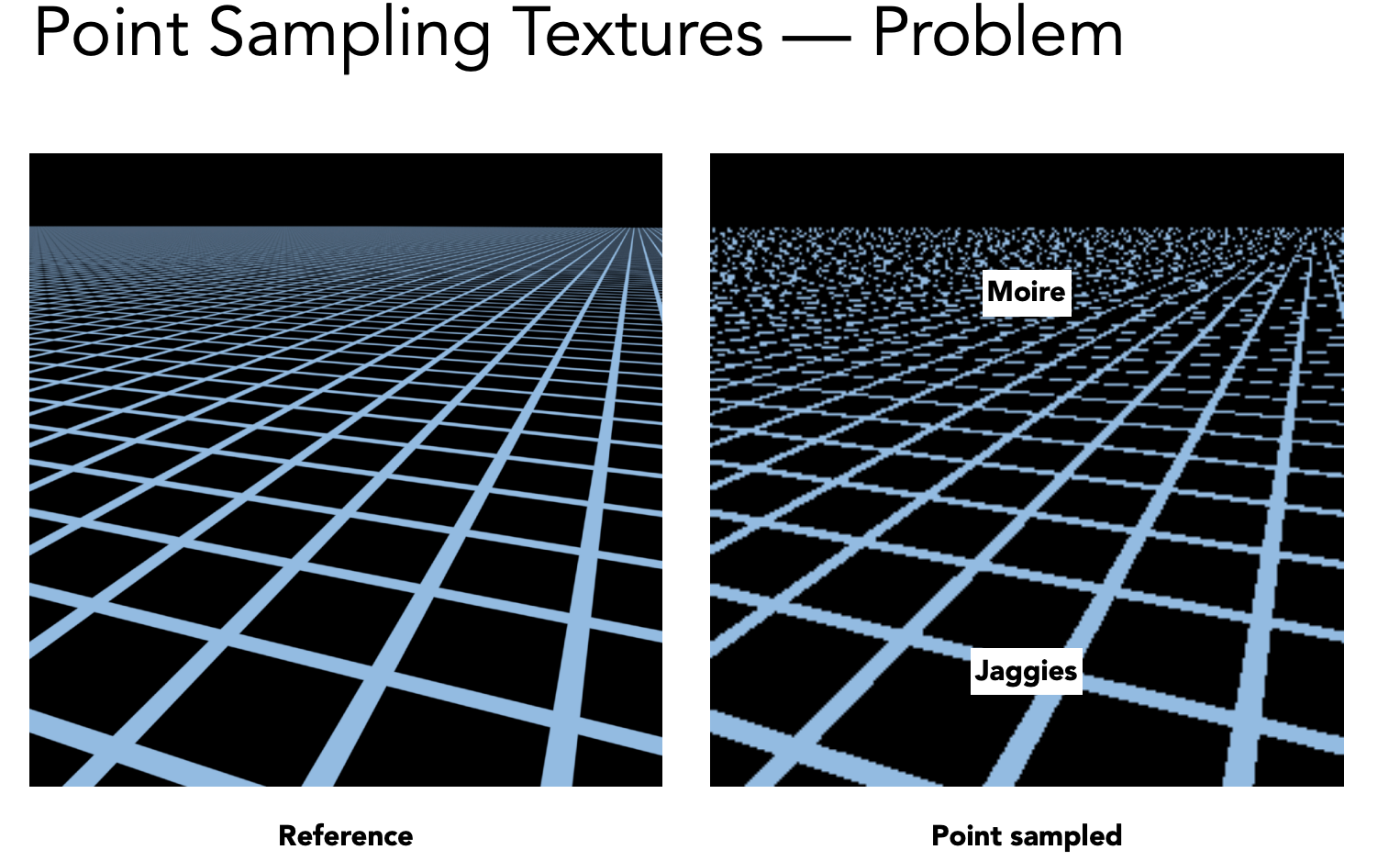
一个像素覆盖多个纹素，直接用像素中心点采样会出现走样问题

​​

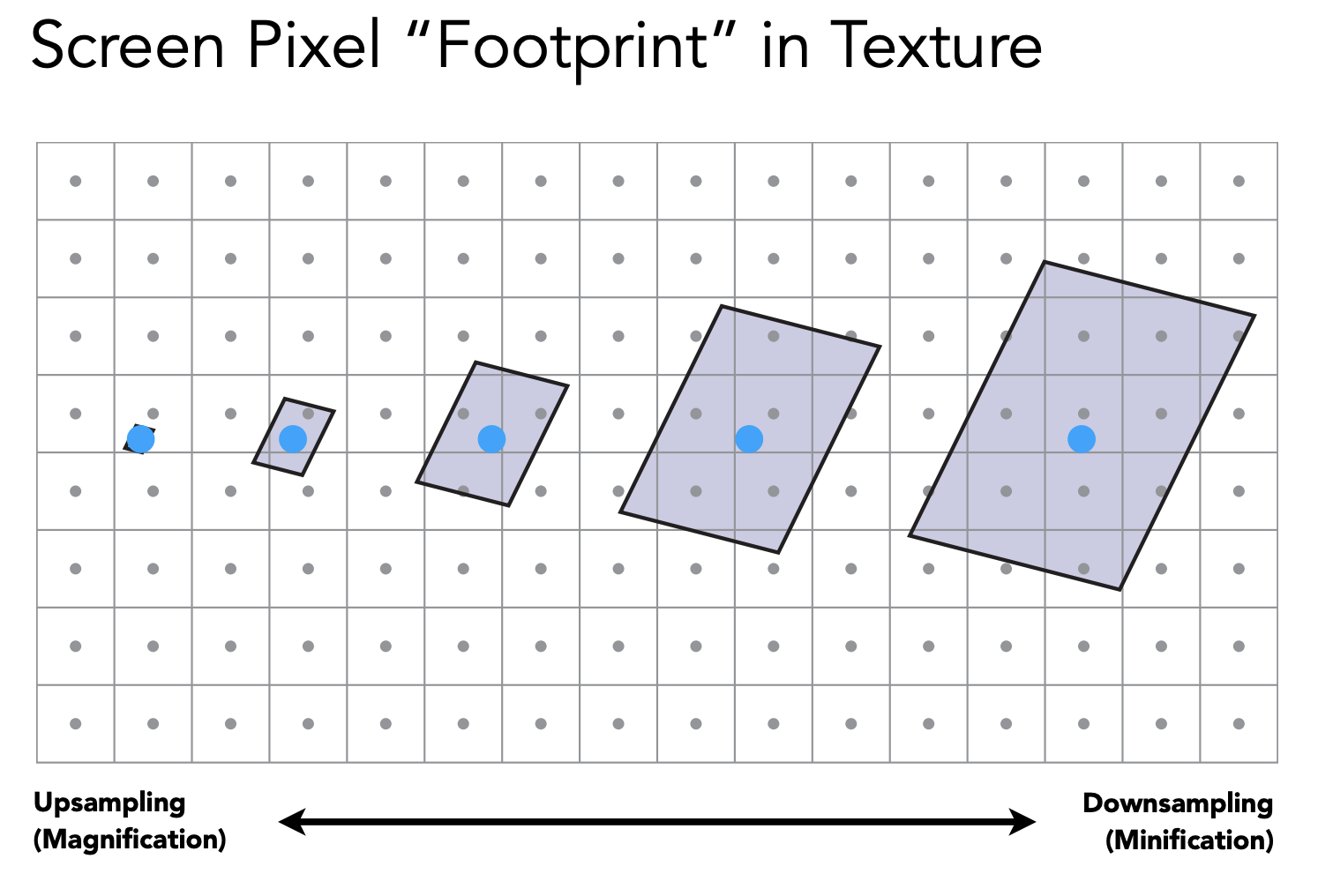
反走样

用超采样的方式，一个像素采用多个采样点进行采样，但这样会造成很大的成本

​​

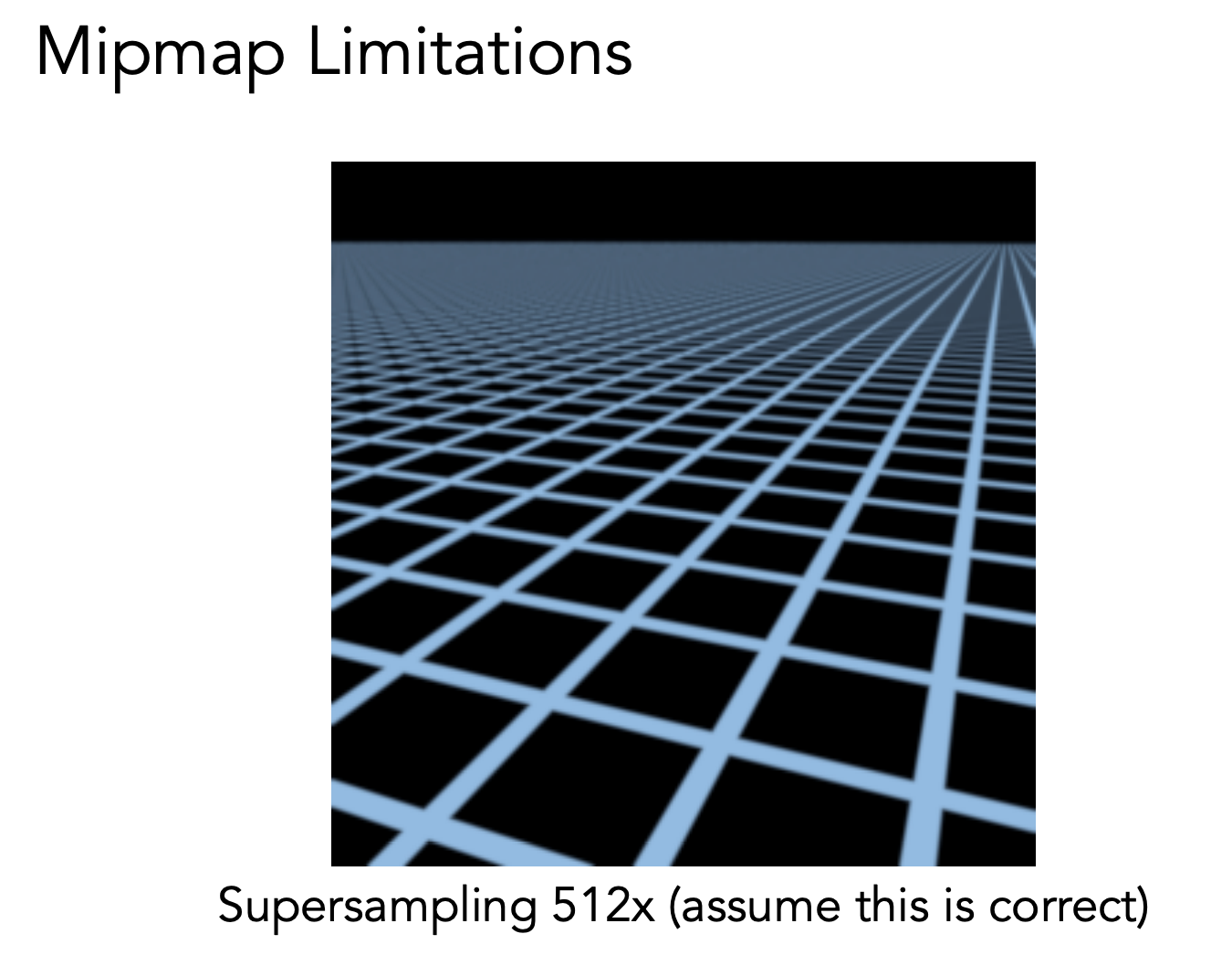
可以采用另一种方式：Range Query，给定一块区域，快速求出其平均值。

Mipmap：快速，近似，正方形的范围查询。

渲染之前，先生成 Mipmap

每层像素小一半

​​

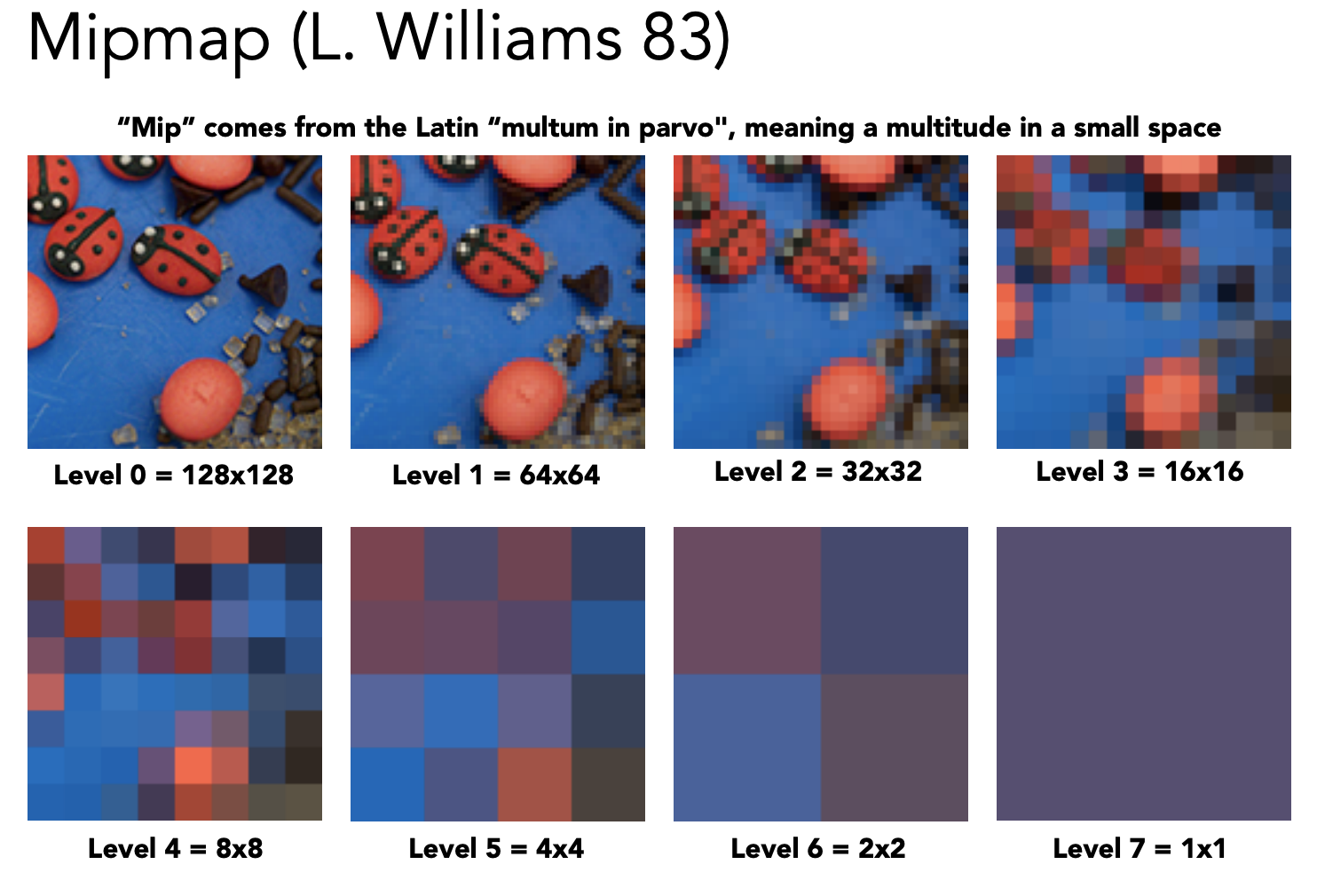
计算机视觉里面会用图像金字塔表示

​​

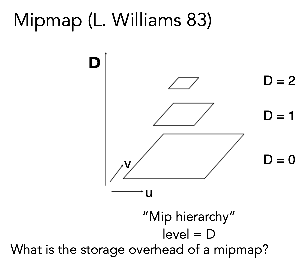
最后的存储量是之前的 3/4。用四个像素中心点投影到纹理坐标，像素点最大的连线模拟纹理坐标中一个对应的一个方形像素的边长。

​​

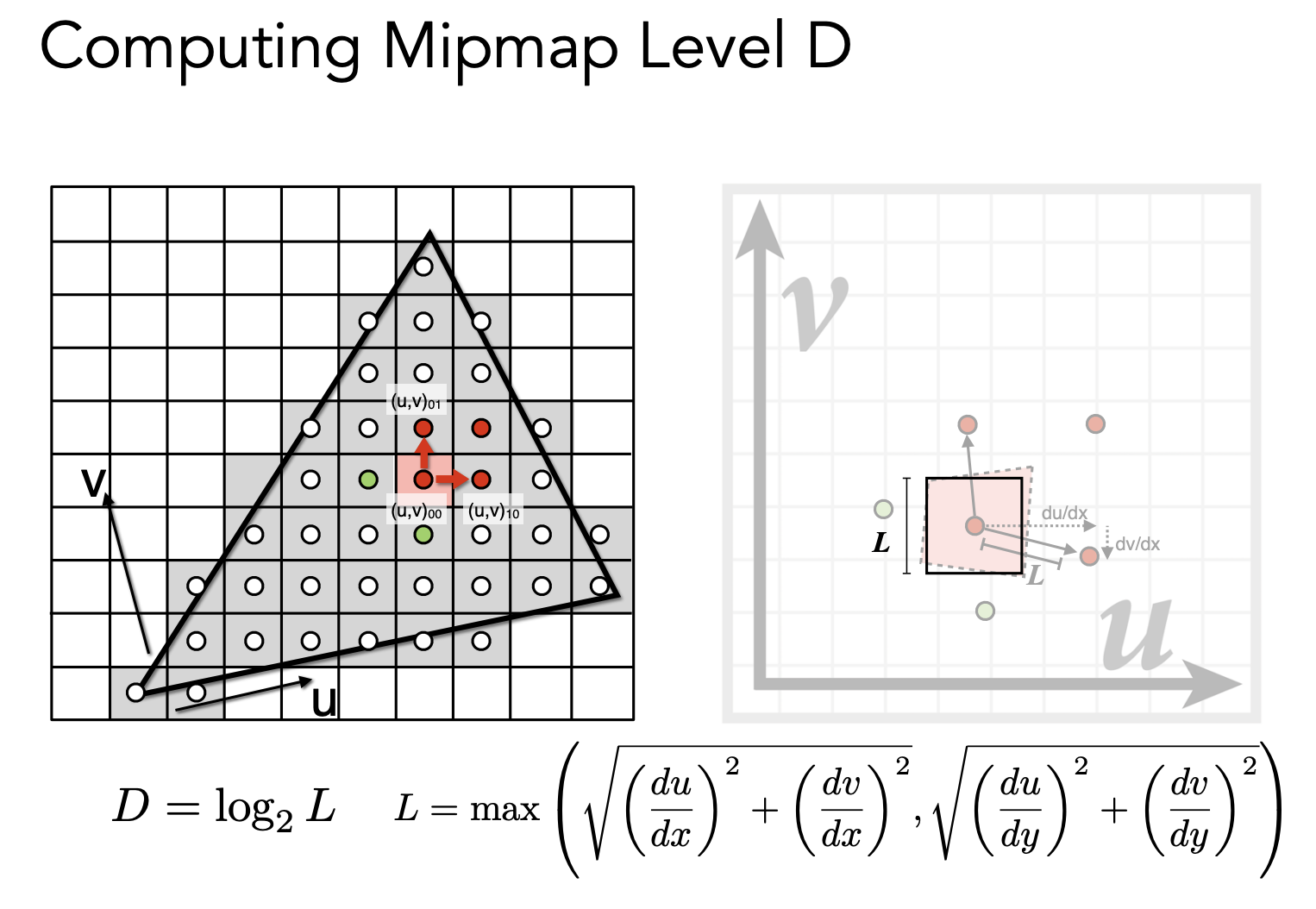
D 是层数，L 是一个屏幕像素对应的纹理像素。求出在第几层一个屏幕像素对应的纹理像素会变成一个像素大小，就用这一层的 MipMap，快速求出范围平均值。

​​

但这样查询可能出现不连续的问题，比如在近的地方用低层，远的地方用高层，但是每一层之间是不连续的。

如果要求两层中间的值，这个时候又可以用双线性插值把两层的结果求出来，再对两层求出来的值合在一起再在层与层之间做线性插值。即三线形插值：

​​

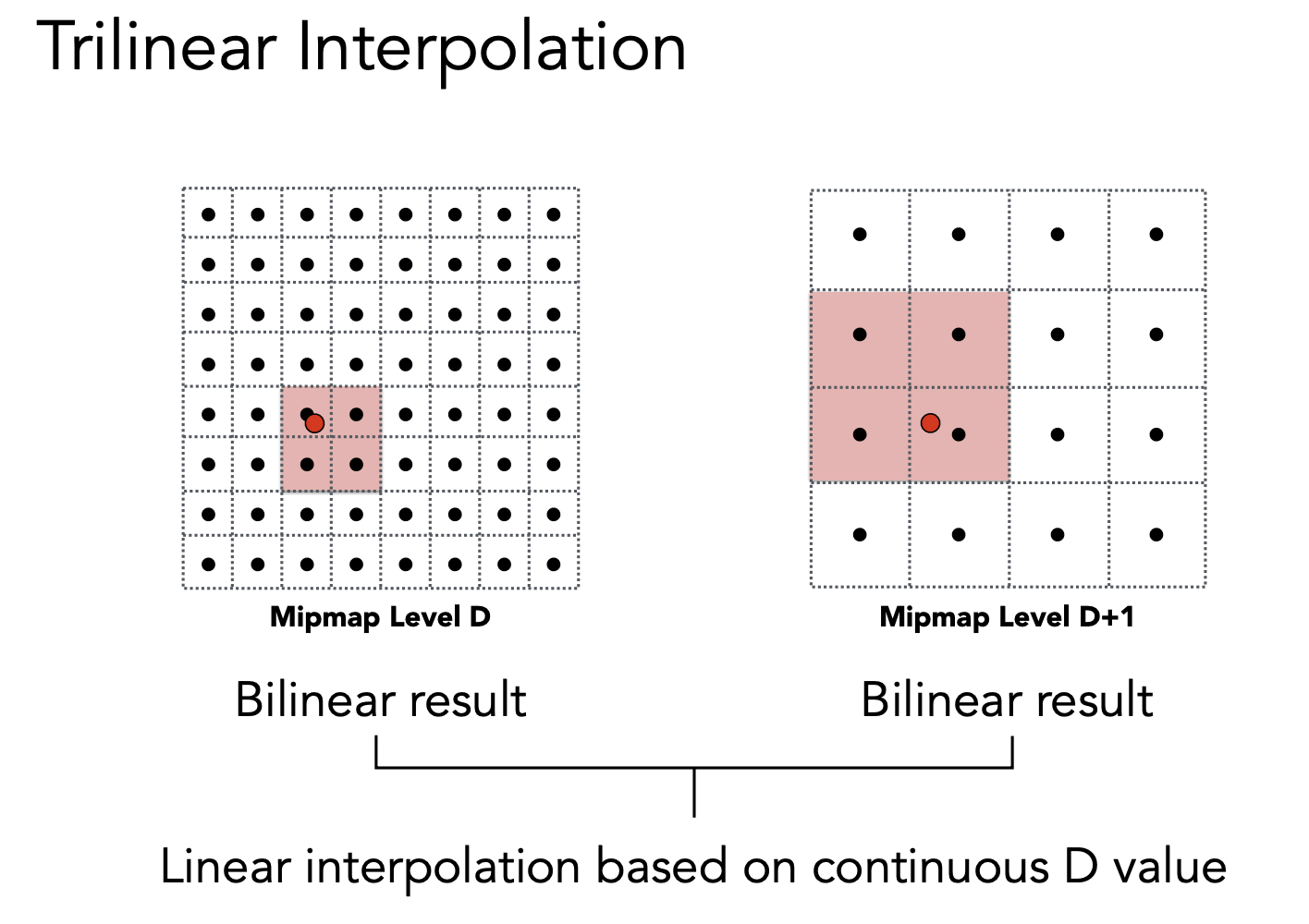
三线形插值的结果就是连续的：

​​

但由于 mipmap 限制在方块区域内，且插值都是近似结果，所以会出现 OverBlur 现象

​​

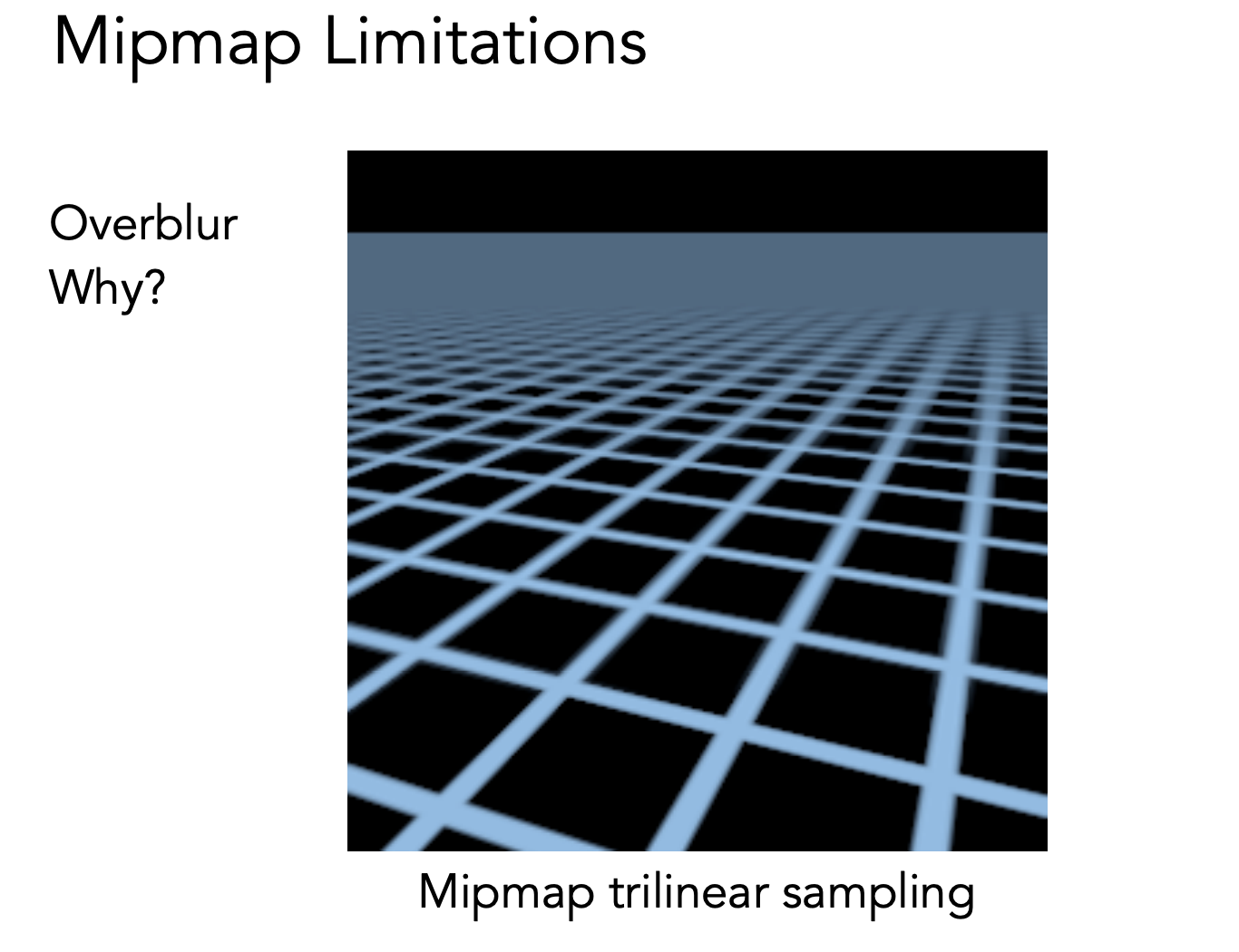
可以用各向异性过滤（Anisotropic）来解决

​​

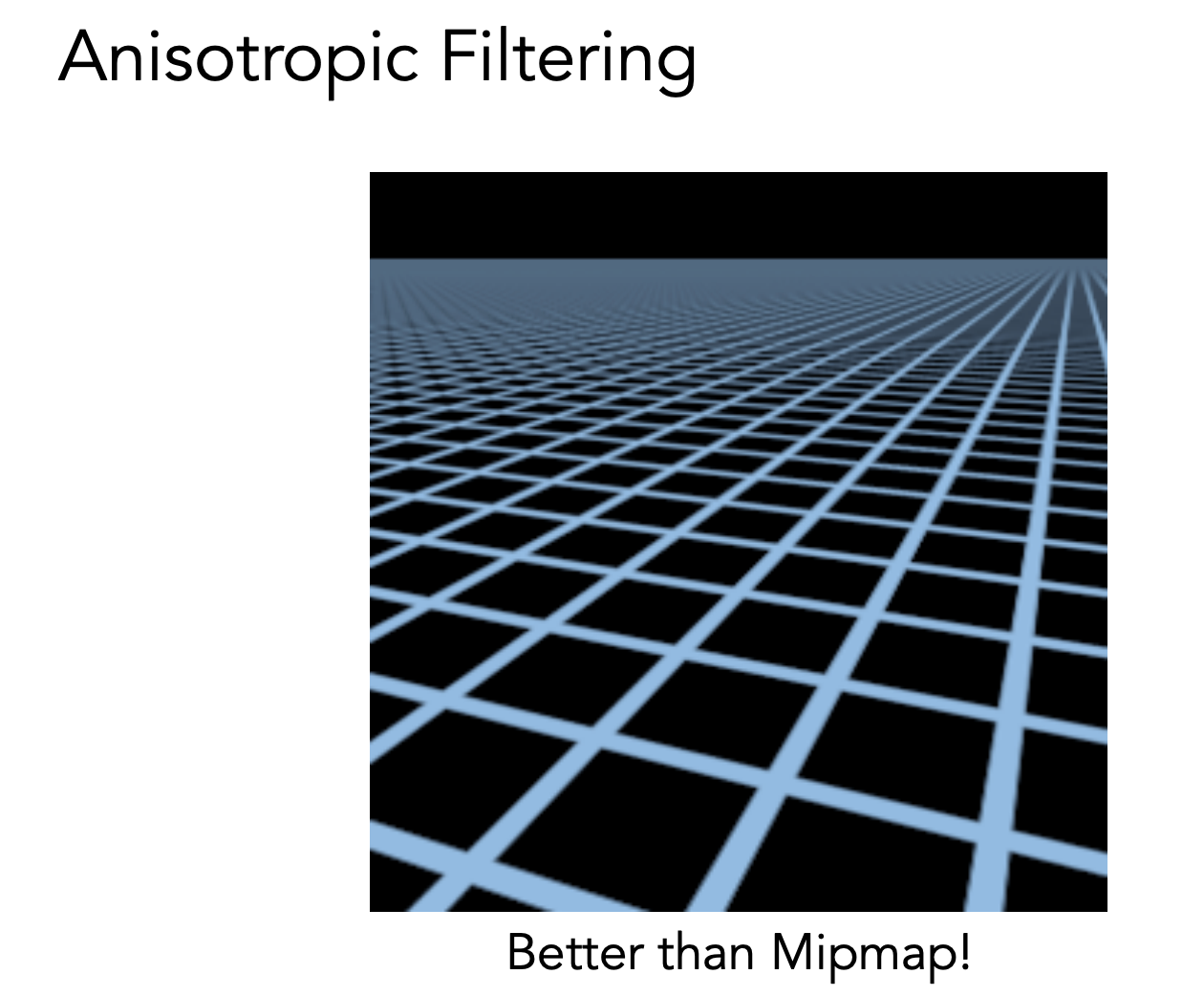
分层时把图片长宽方向压缩，这样屏幕像素就可以对应纹理坐标系中的一个矩形区域，而不局限于一个方形区域。

​​

各向异性过滤（RipMaps）要三倍的额外存储空间

​​

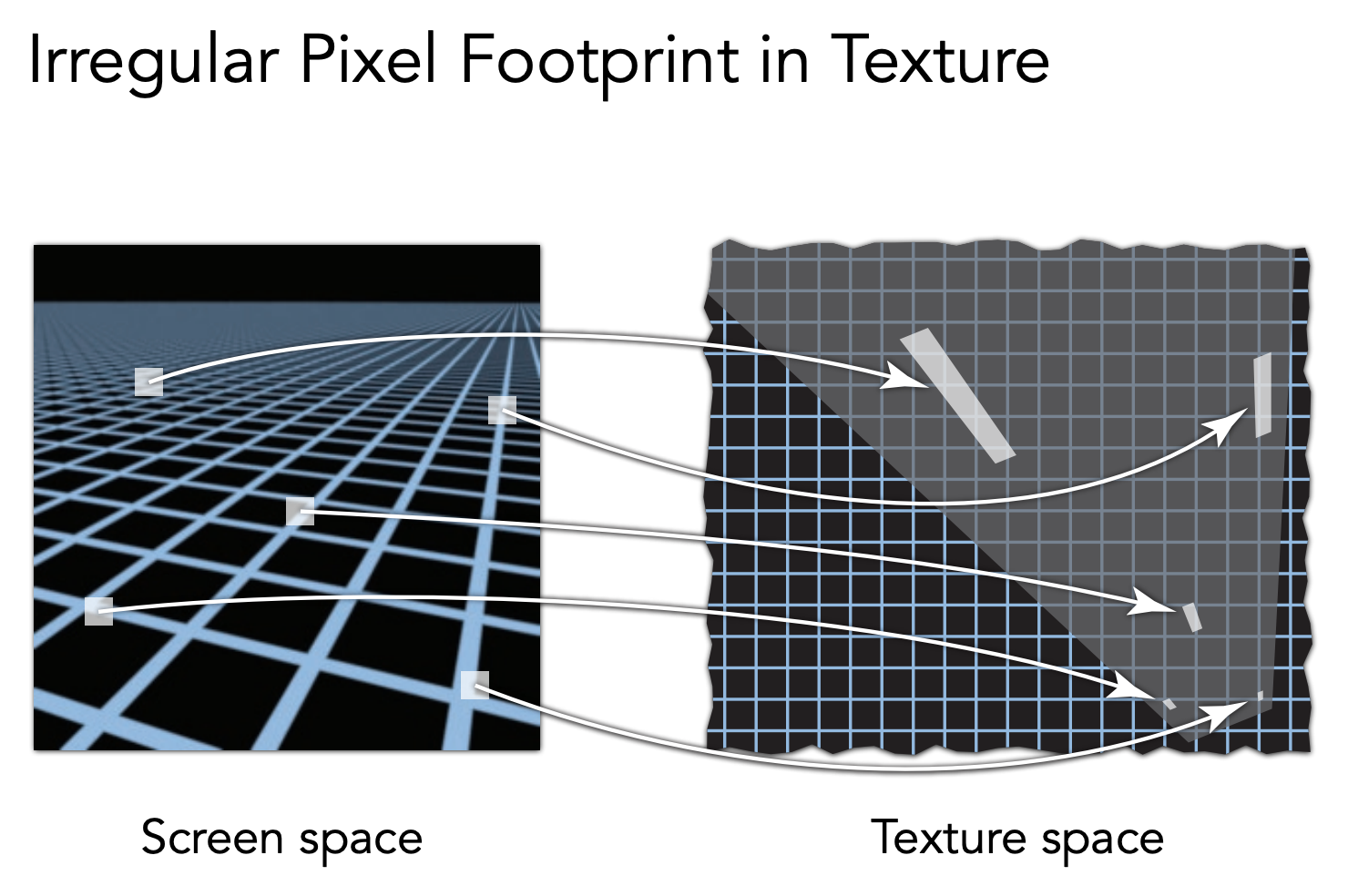
对于斜着的矩形区域还是不能正常模拟，因此还有其他的过滤方式：

EWA 过滤

任意一个不规则的形状都可以拆成多个圆形，覆盖在不规则的形状上，每次查询一个圆形，多次查询。

​​