第三章:变换
变换
本章学习内容:
- 为什么学习变换
- 2 维空间变换:旋转、缩放和切片
- 齐次坐标
- 变换组合(不同的变换组合形新的变换)
- 3 维空间变换
为什么学习变换
变换分为:模型变换、视图变换
变换的重要应用:
modeling translation:描述摄像机的运动(位置移动)
modeling rotation:机器人动画关节转动,逆运动学
modeling scale:皮克斯开场动画
viewing:3 维到 2 维投影
二维变换
scale matrix 缩放
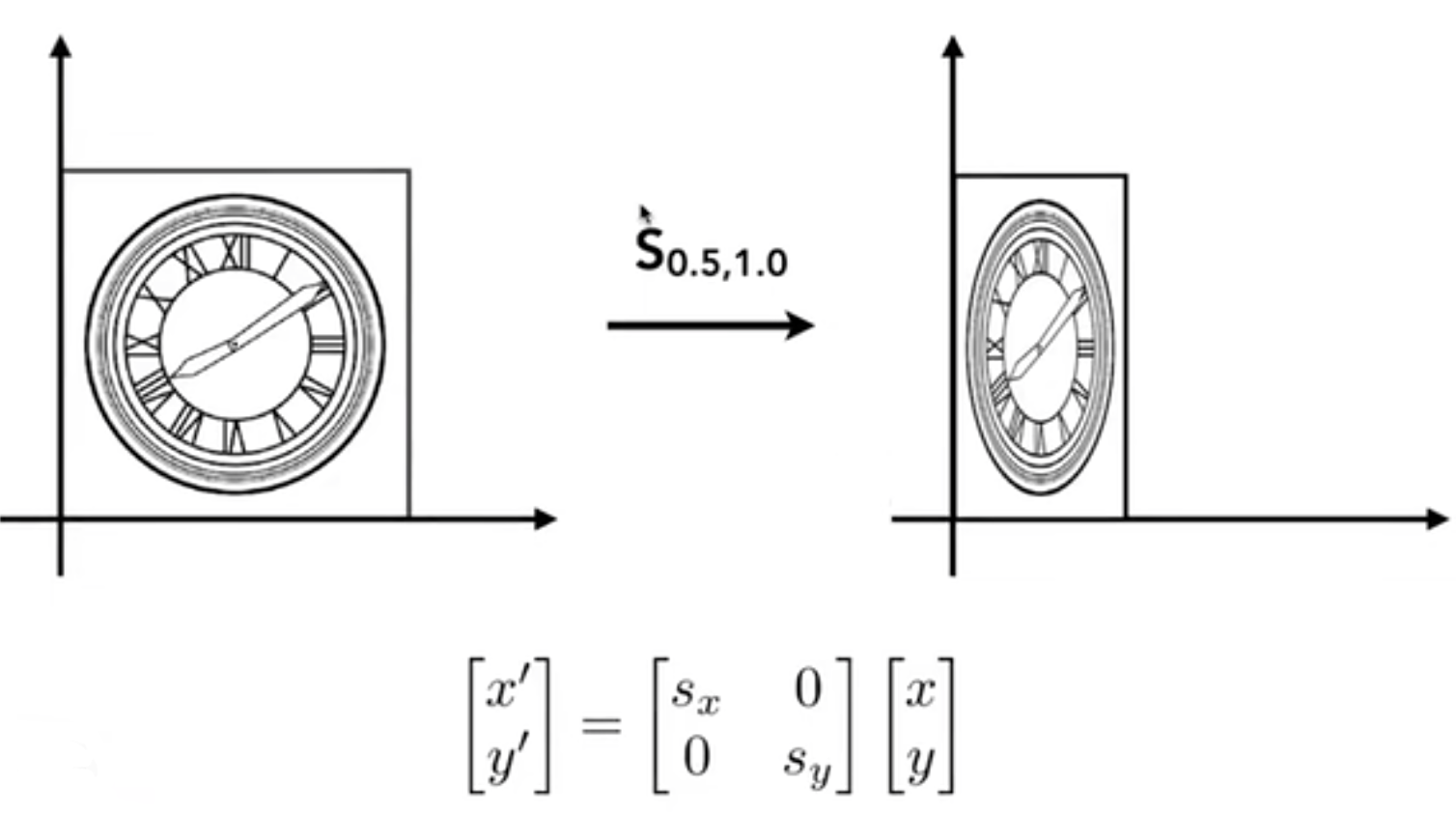
reflection matrix 反射(对称)
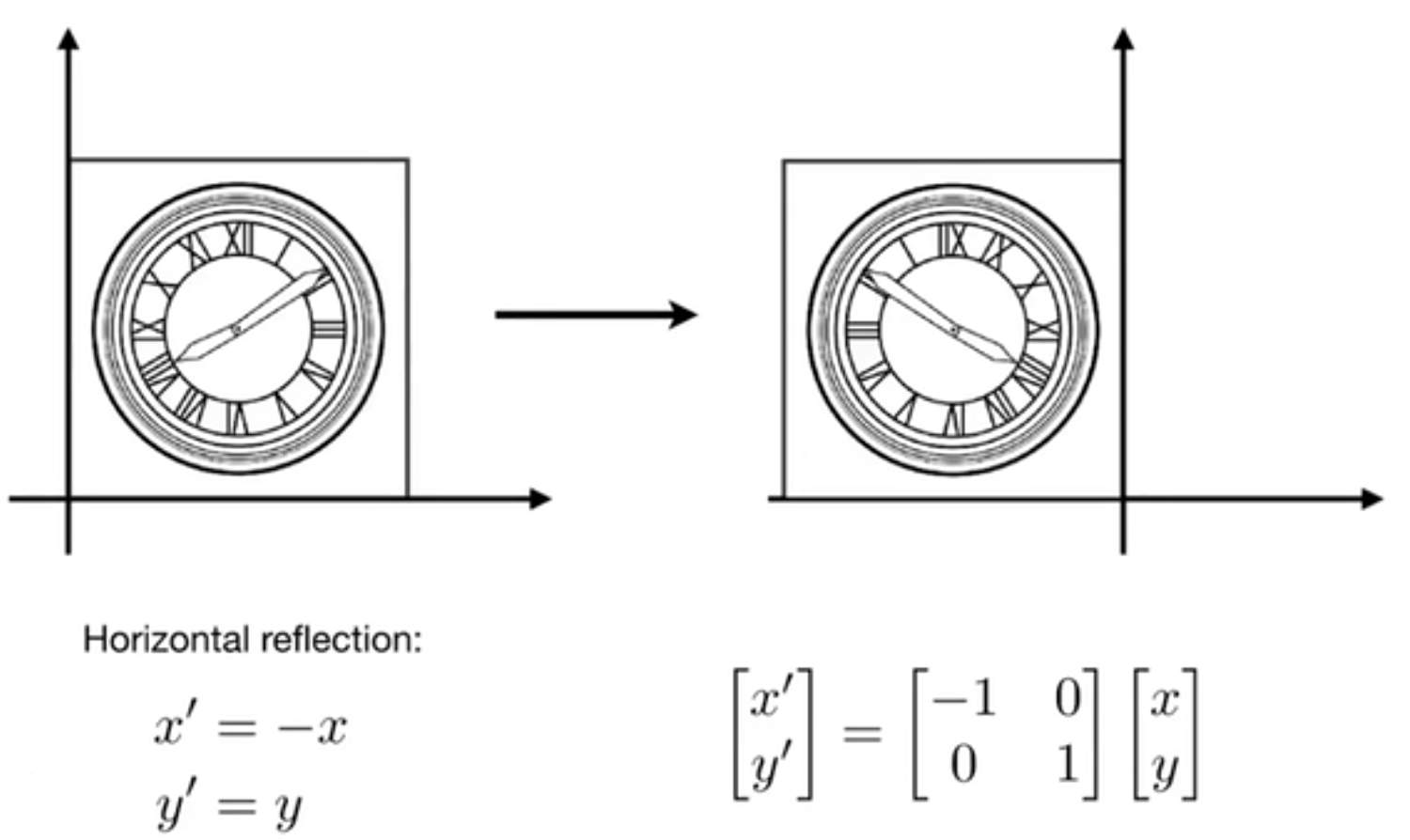
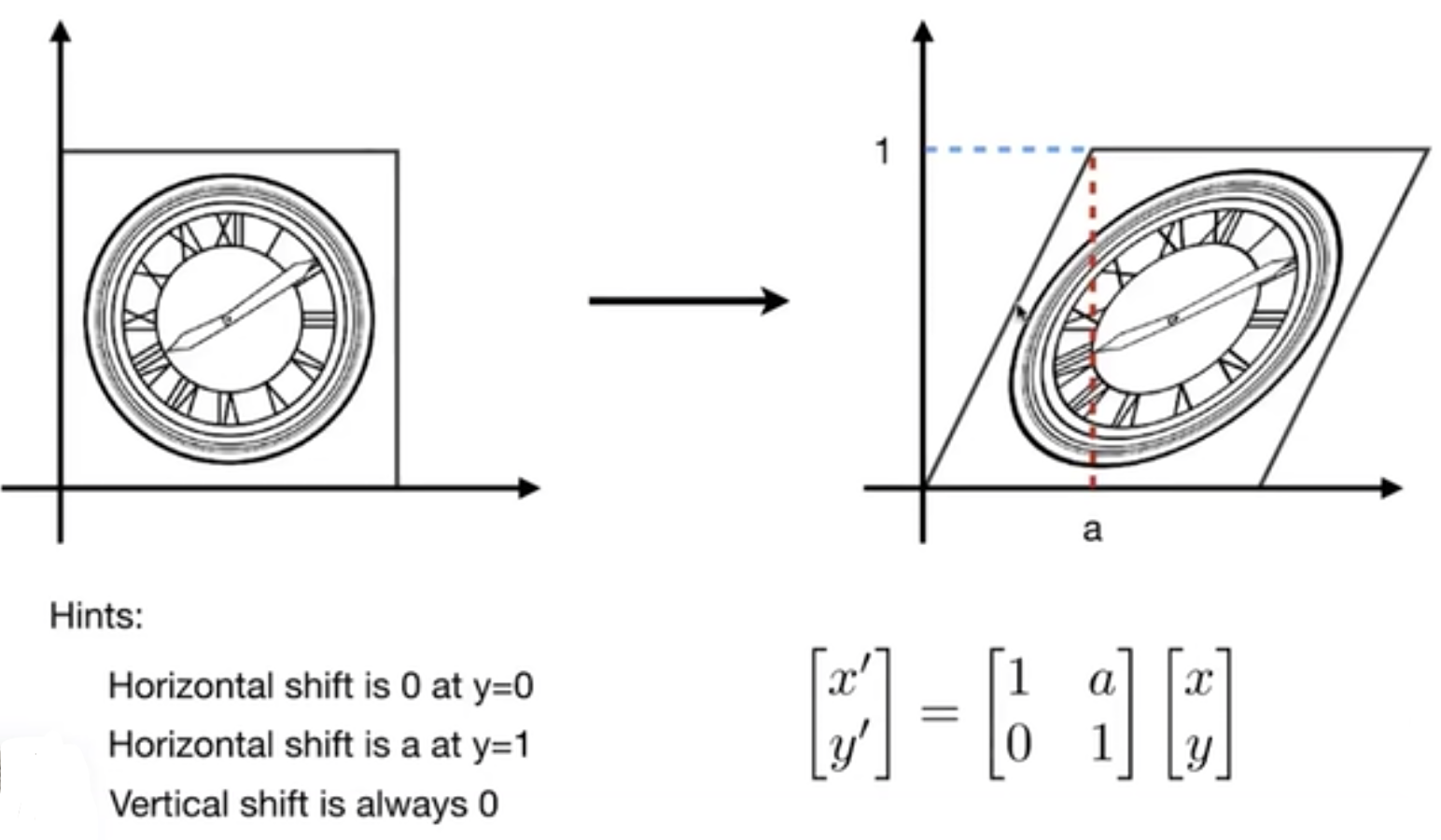
shear matrix 切变
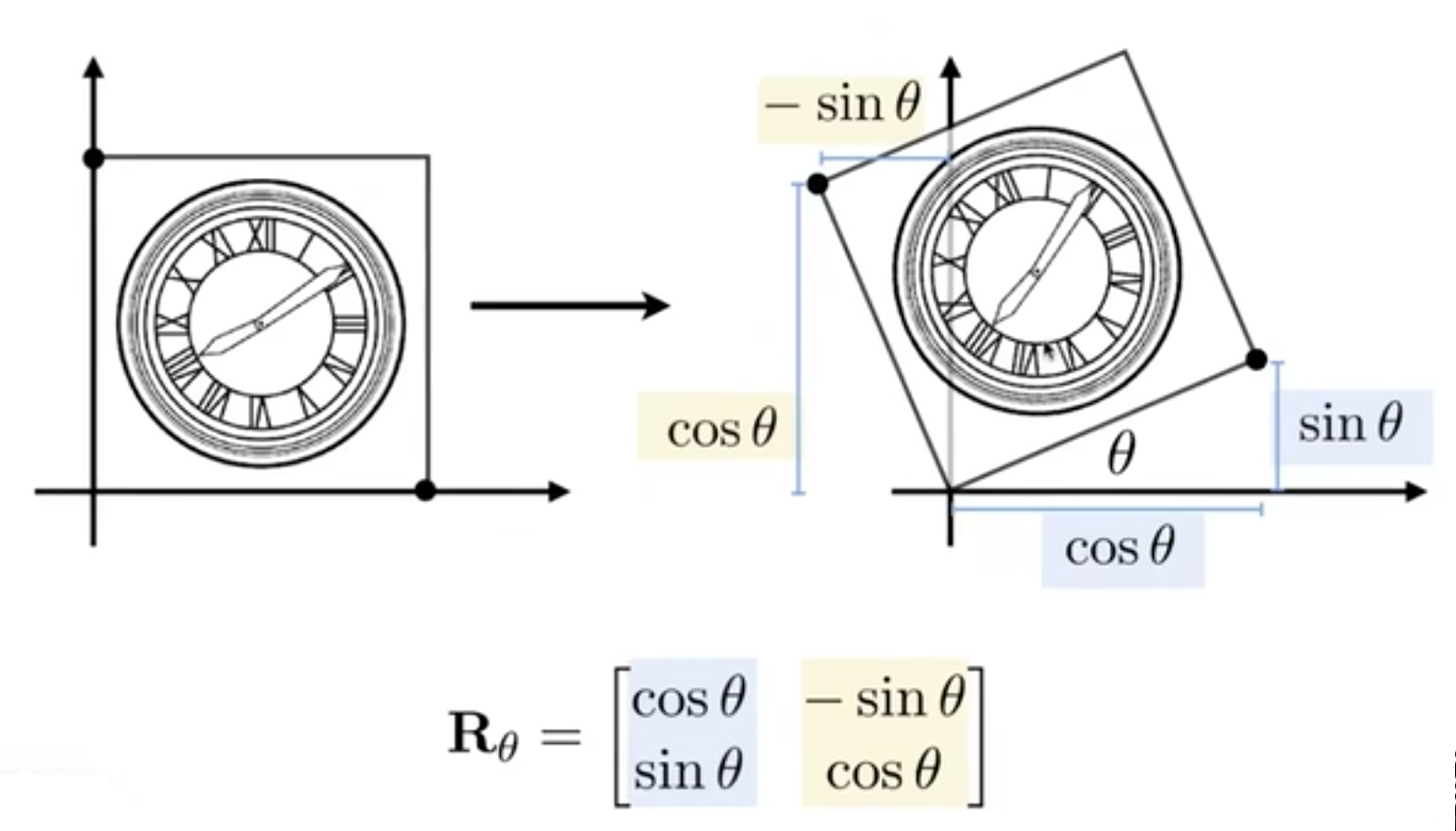
rotation matrix 旋转
(同维度的)矩阵乘输入坐标可以得到输出到坐标叫做线性变换
齐次坐标
平移变换不能直接表示为矩阵乘坐标,需要加一个向量
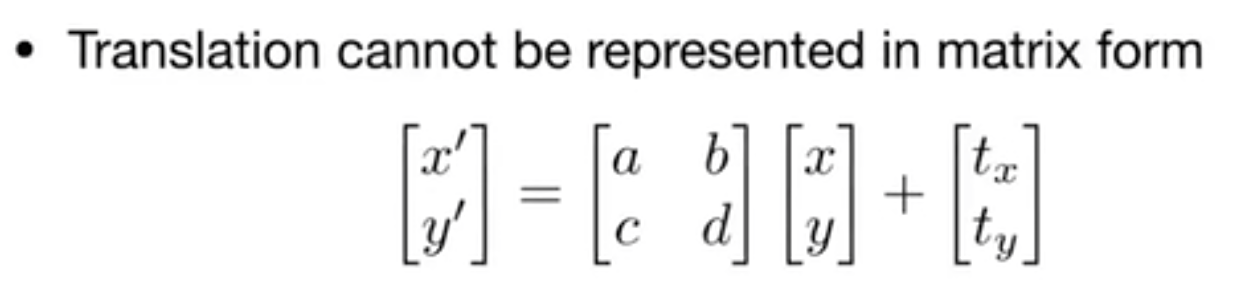
引入齐次坐标是为了找到一个解决方法统一表示二维变换


线性变化 + 平移可以统称为仿射变换,这种仿射变换都可以都可以转换为齐次坐标的形式。用一个矩阵可以统一所有的操作
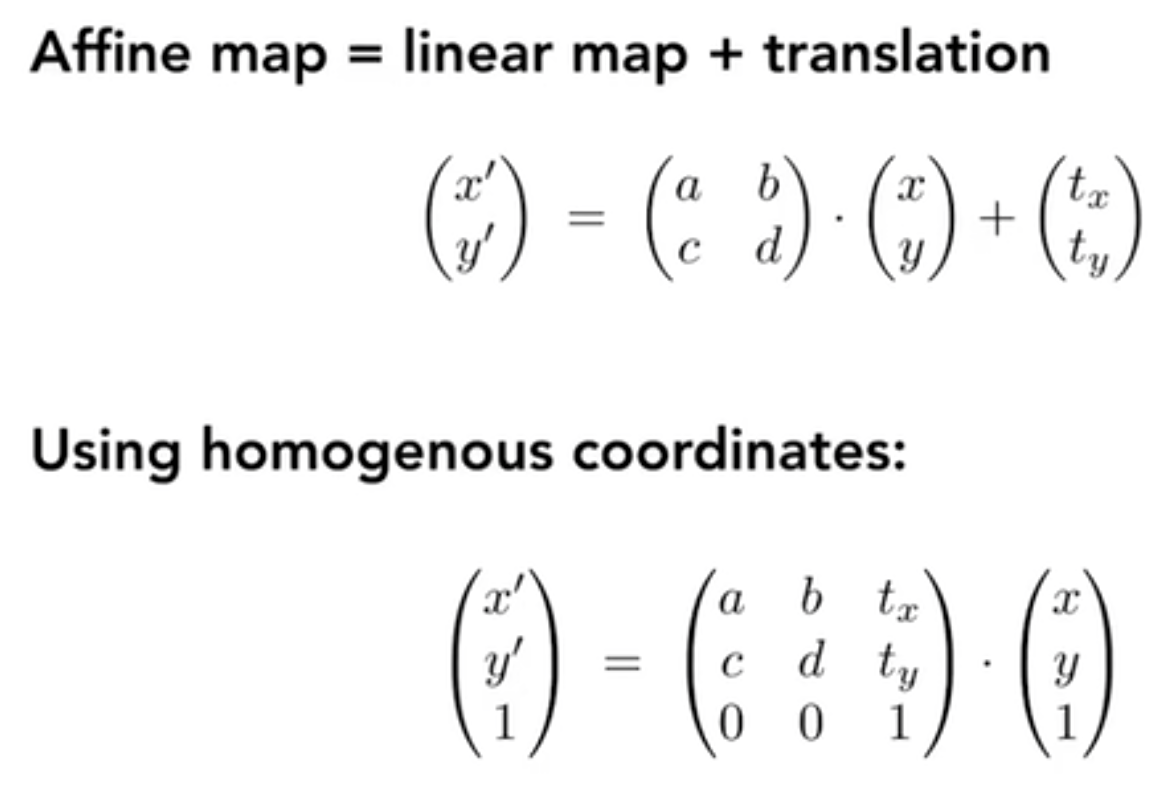
最后一行永远是 0 0 1

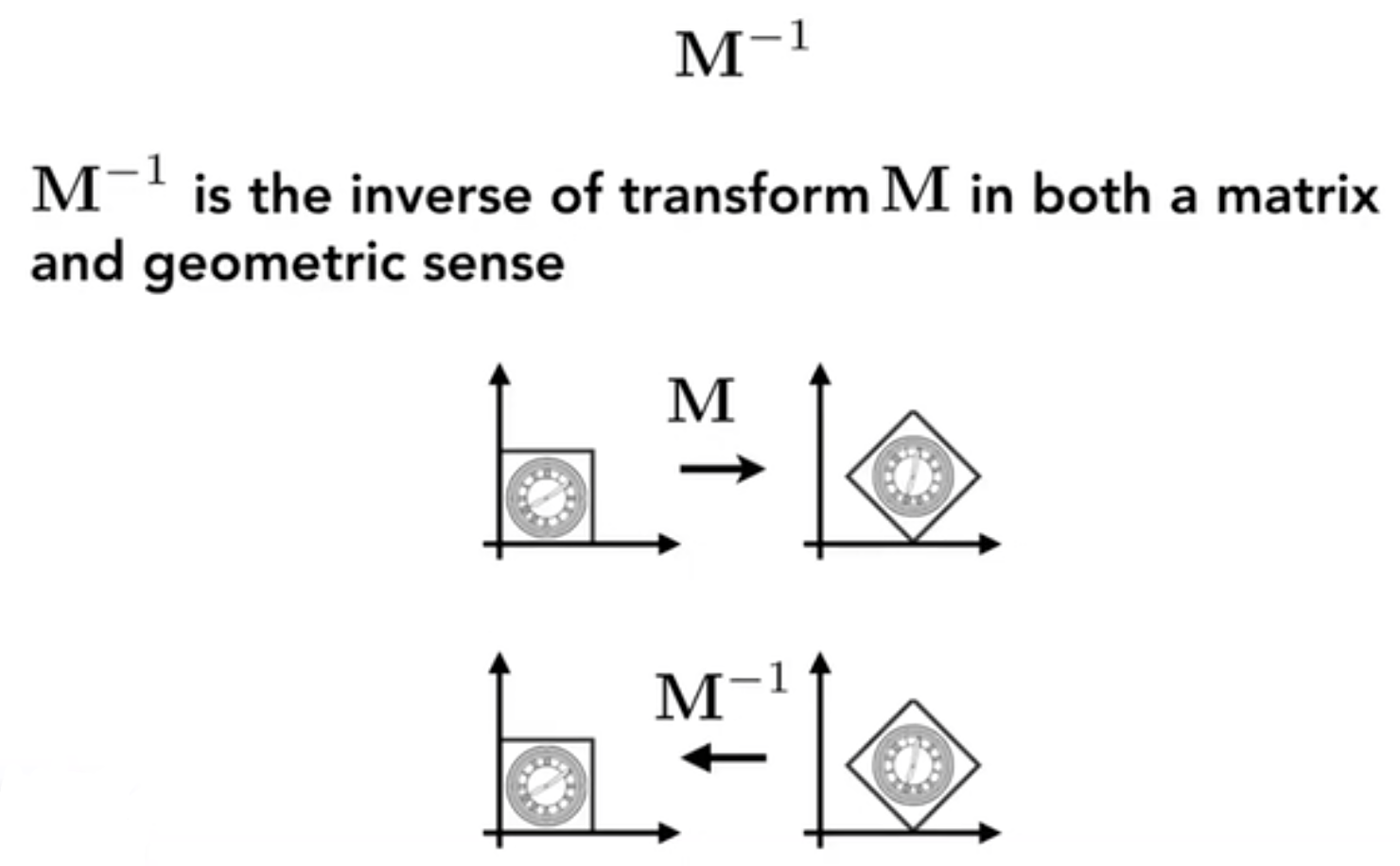
逆变换(变换操作反过来,乘以变换的逆矩阵)
变换组合
先平移再旋转
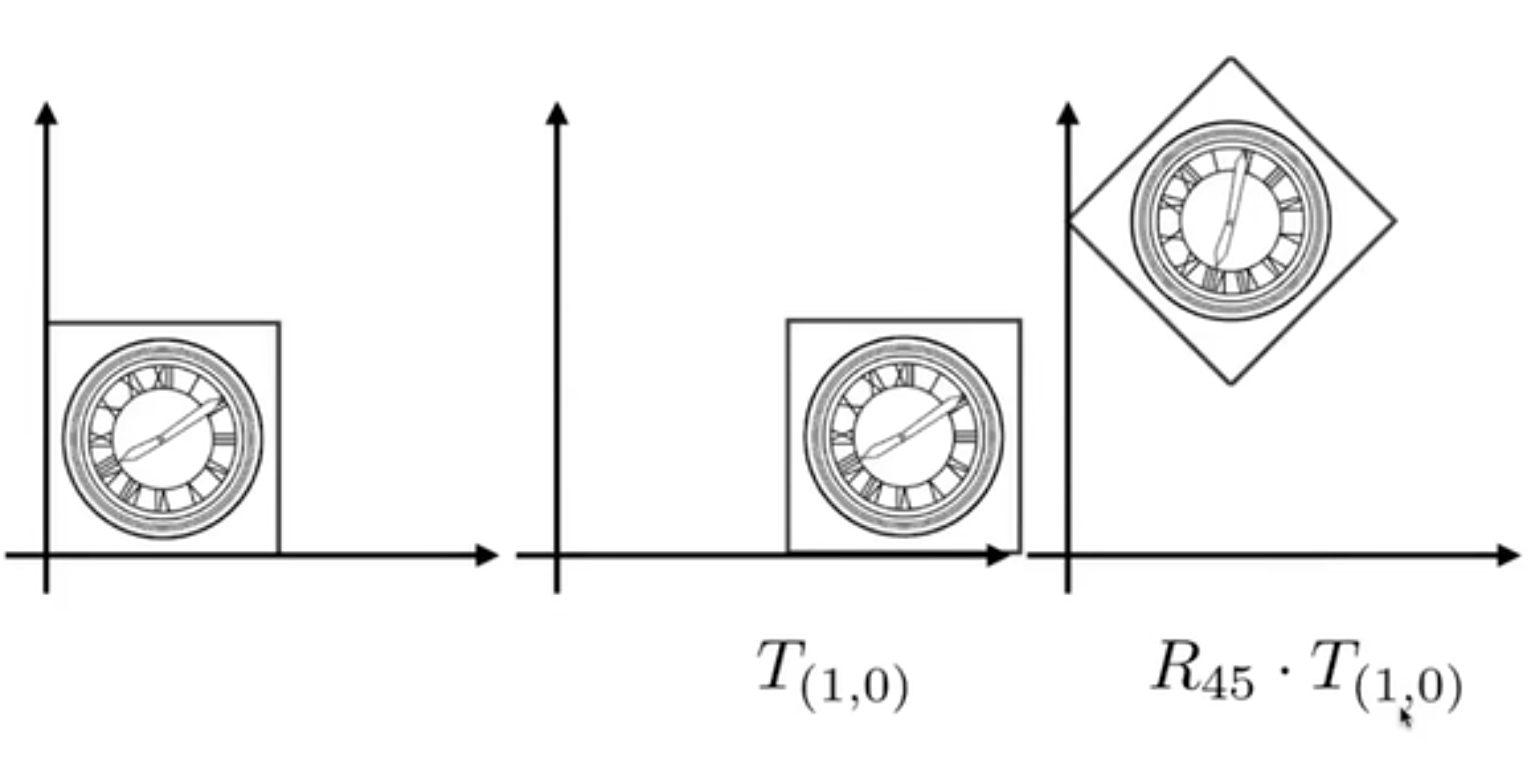
先旋转再平移
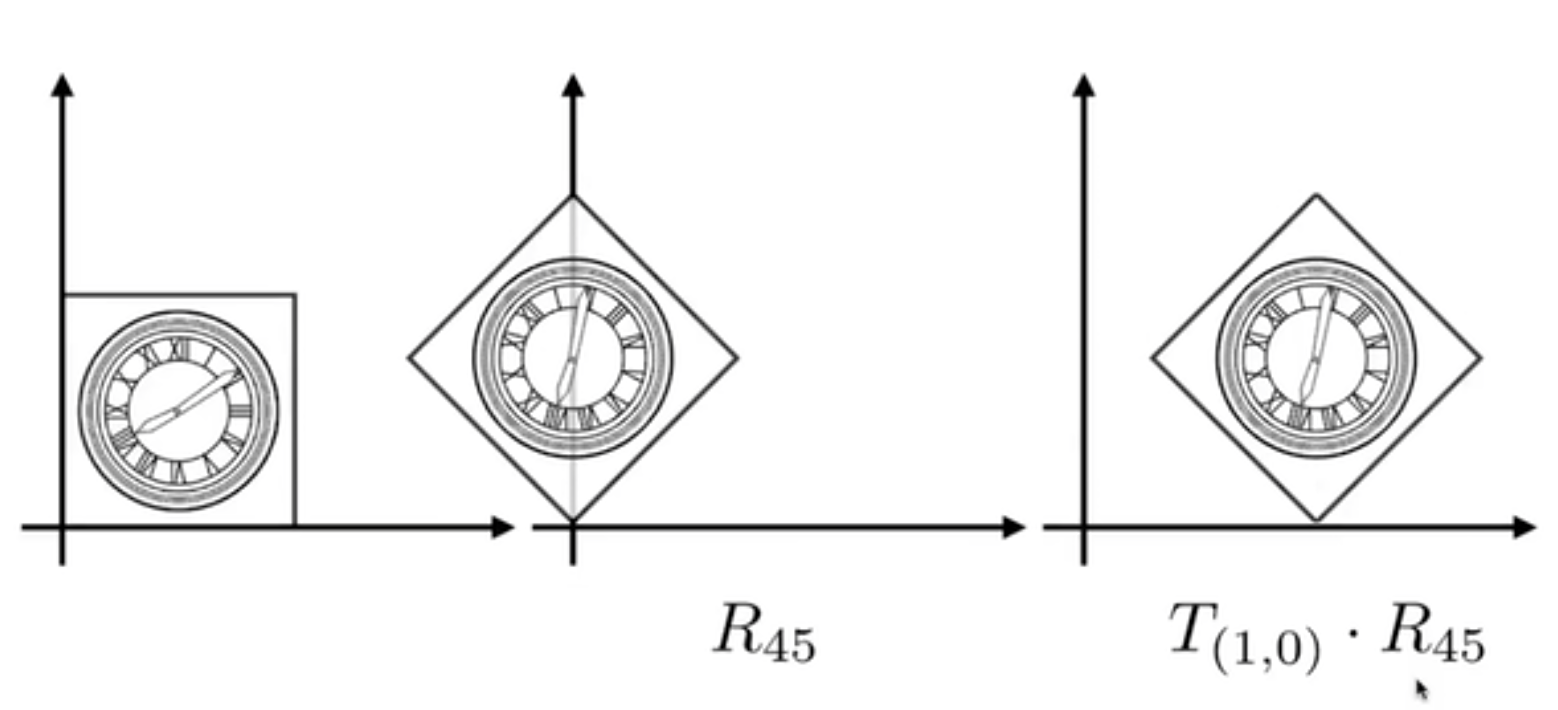
复杂的变换可以通过简单的变换得到
变换的顺序非常重要(矩阵乘法的顺序影响结果)
变换组合从右到左应用矩阵


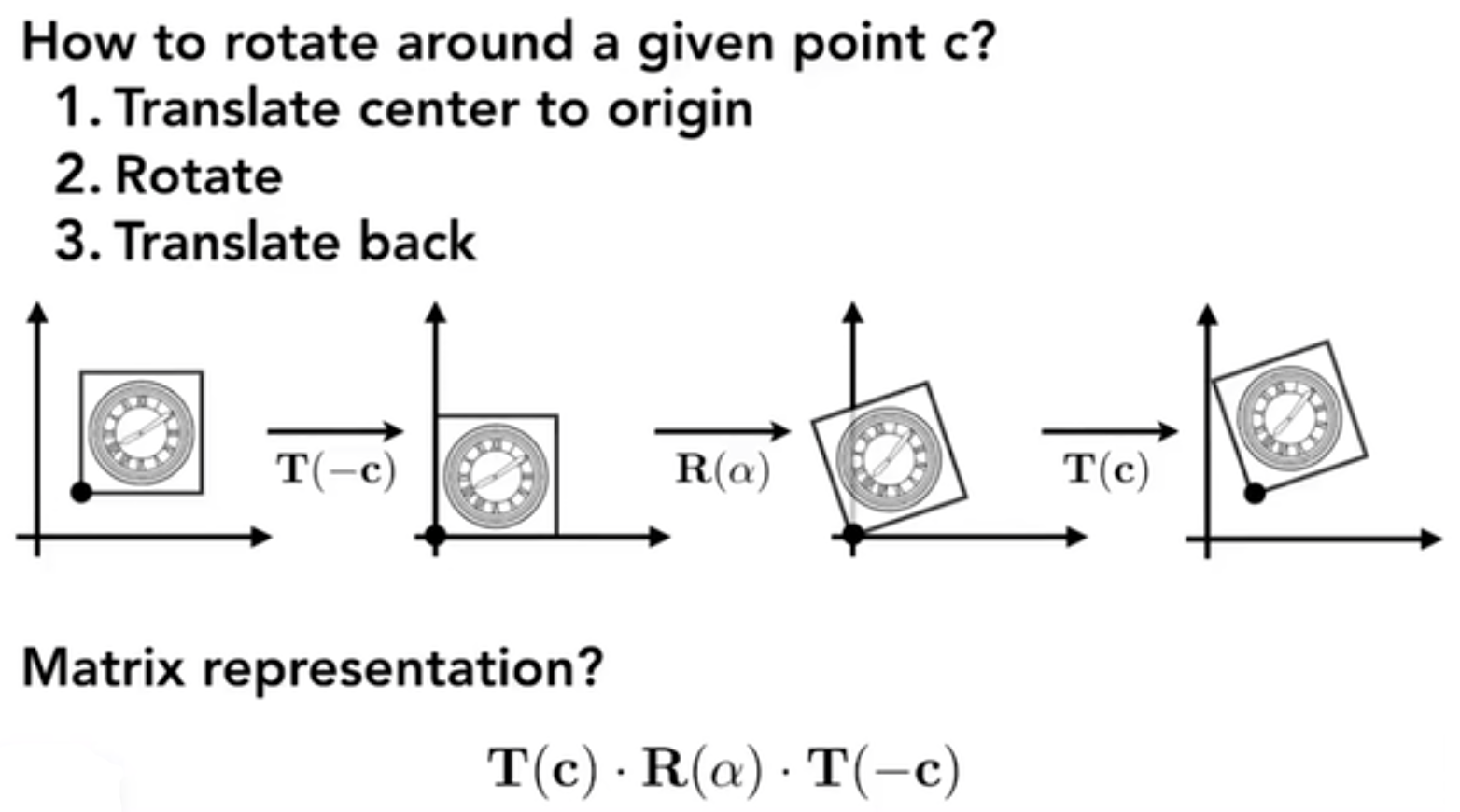
变换分解
如果希望在非原点旋转,可以把旋转点平移到原点后再进行旋转,旋转后再平移回去
三维变换
与 2 维类似
