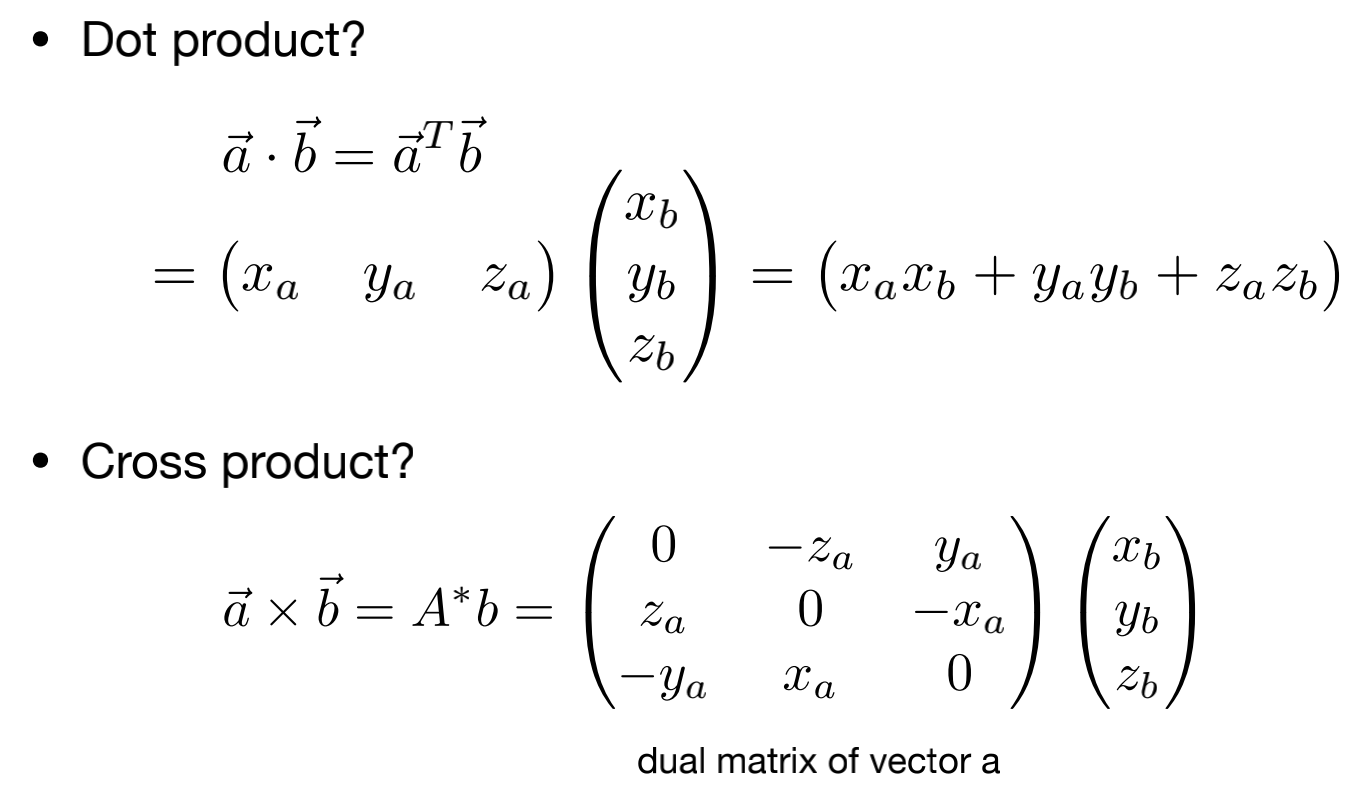第一、二章：图形学概述、向量与线性代数

第一章 图形学概述

1.图形学应用场景

游戏场景渲染、电影特效、动画、设计、可视化（人体三维扫描）、虚拟现实、数字绘图、模拟、GUI、字体排版等

2.图形学包含内容：

• 数学：矩阵、曲线、曲面

• 物理学：光学、着色

• 描述、操作三维的不同形体

• 动画、仿真

3.本课程包含的内容：

• 光栅化

  • 光栅化是把三维空间的几何形体显示在屏幕上，是实时图形学的主要应用。实时：每秒钟生成 30 帧，否则叫做离线

• 曲线、曲面

  • 如何表示一条光滑的曲线、如何表示曲面、怎么把简单曲面通过细分的方法得到更复杂的曲面，形状发生变化的时候面要如何变化，如何保持物体的拓扑结构

• 光线追踪

  • 实时光线追踪技术

• 动画/模拟

4.本课程不包含的内容：

• 怎么使用 API

• 怎么做三维建模

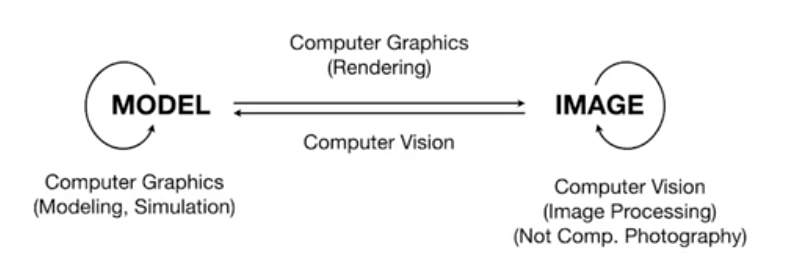
• 计算机视觉：一切需要猜测的东西是计算机视觉（根据图像推测模型）。

  ​​​​

  model 描述三维空间中形状的几何形体，或对于渲染而言描述它的材质、光照，把这些三维空间中有的东西转为一幅图（渲染），就是计算机图形学。此外，还包括纯三维空间的仿真，材质建模、材质与光线之间作用的研究等，都属于计算机图形学的范畴。

从一张图识别出各种模型（比如识别出照片里哪些是桌子、椅子），或者图形、视频处理（中间涉及到一些推测、推理）等是计算机视觉的范畴。

某些场景下没有严格的边界，比如 AR 需要二者的结合。

第二章 向量与线性代数

1.图形学依赖：

• 数学基础：线性代数、微积分、统计

• 数学基础：力学、光学

• 其他杂项：信号处理、数值分析

• 一点点美学

2.向量（Vectors）

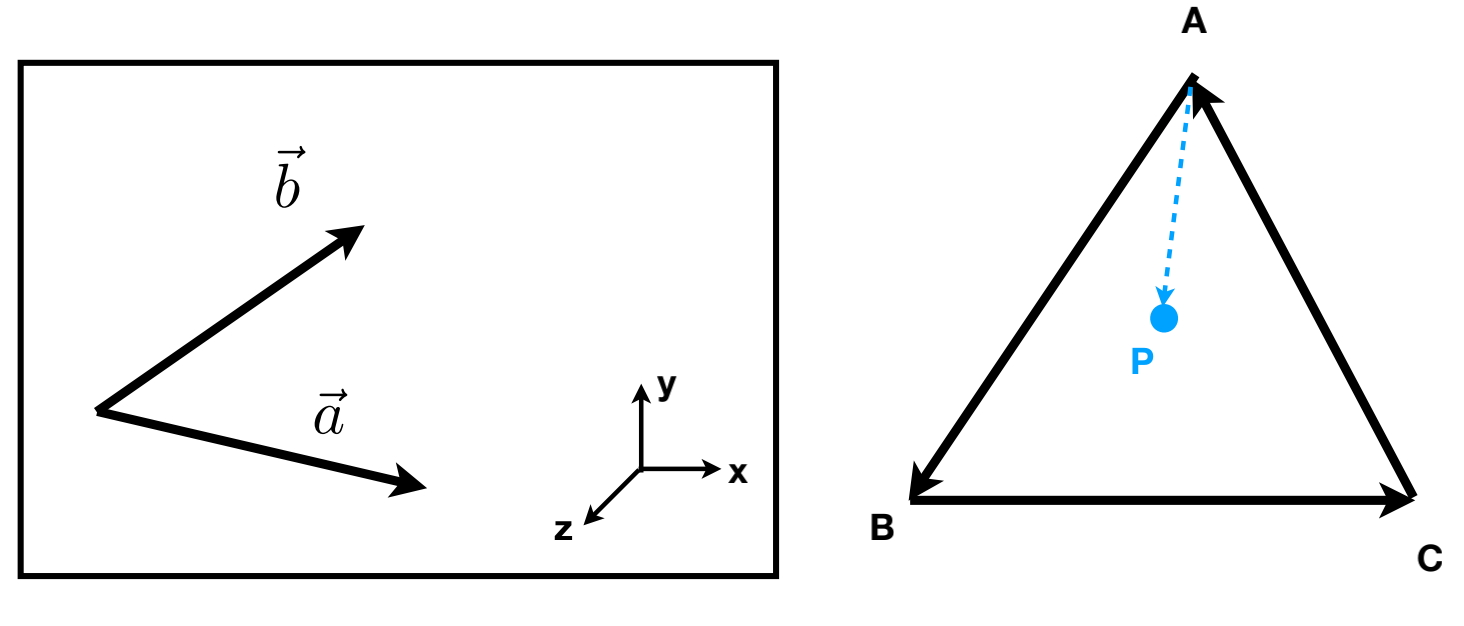
向量表示两个内容：方向和长度，平移向量不会改变它（因为方向和长度不变）。

​​

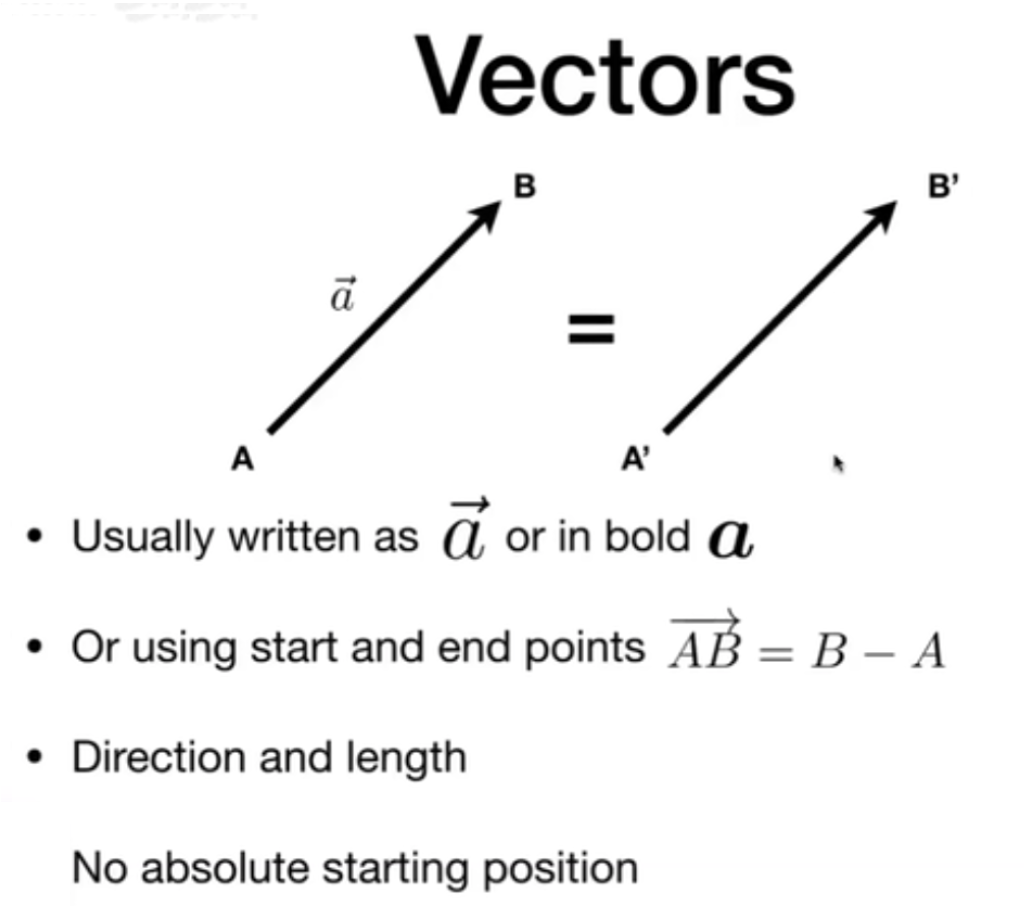
一个向量除它的长度可以得到一个长度为 1 的单位向量。

​​

向量求和：

几何上：平行四边形法则、三角形法则。

​​

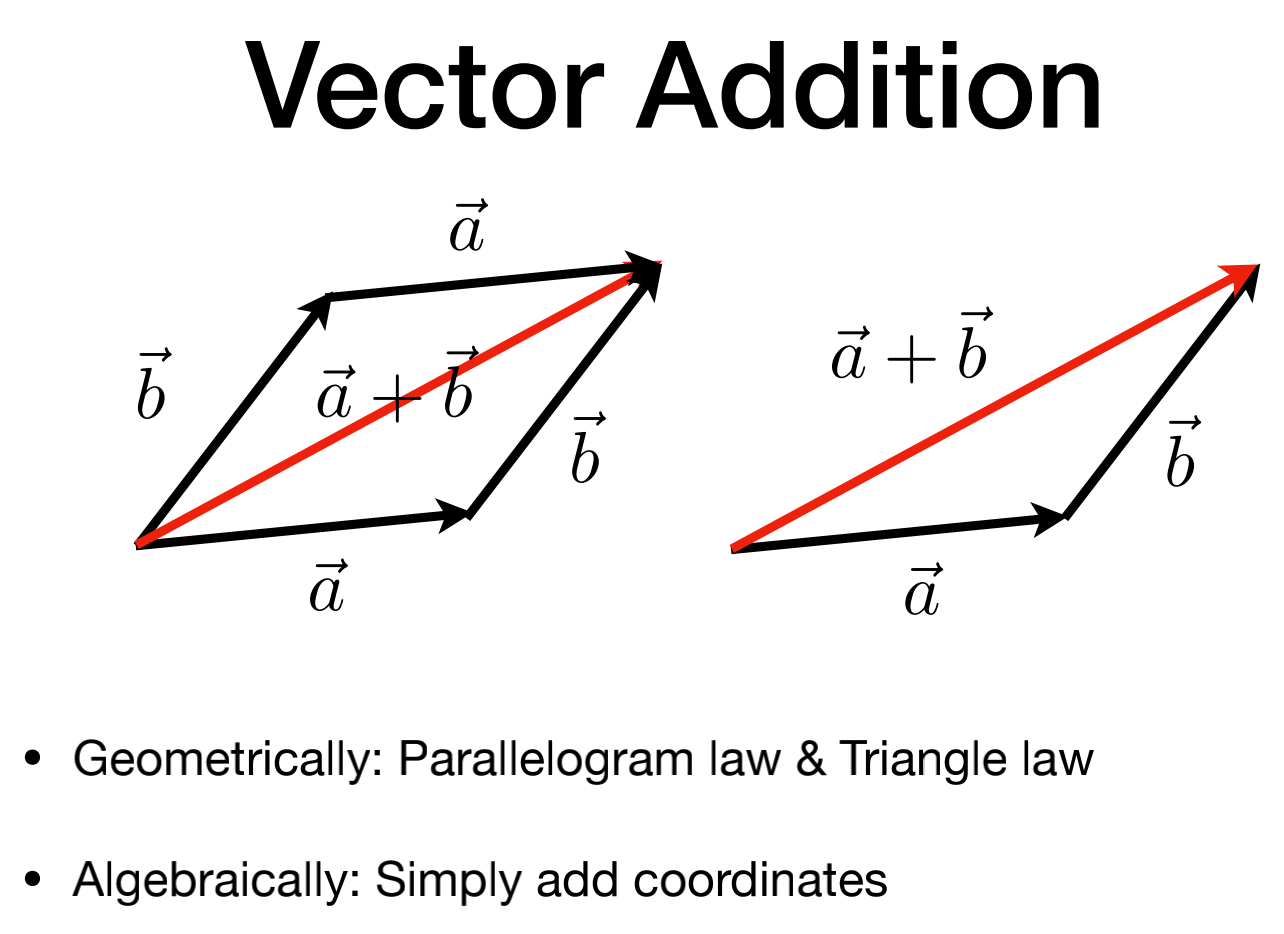
代数上：坐标相加（笛卡尔坐标系）

​​

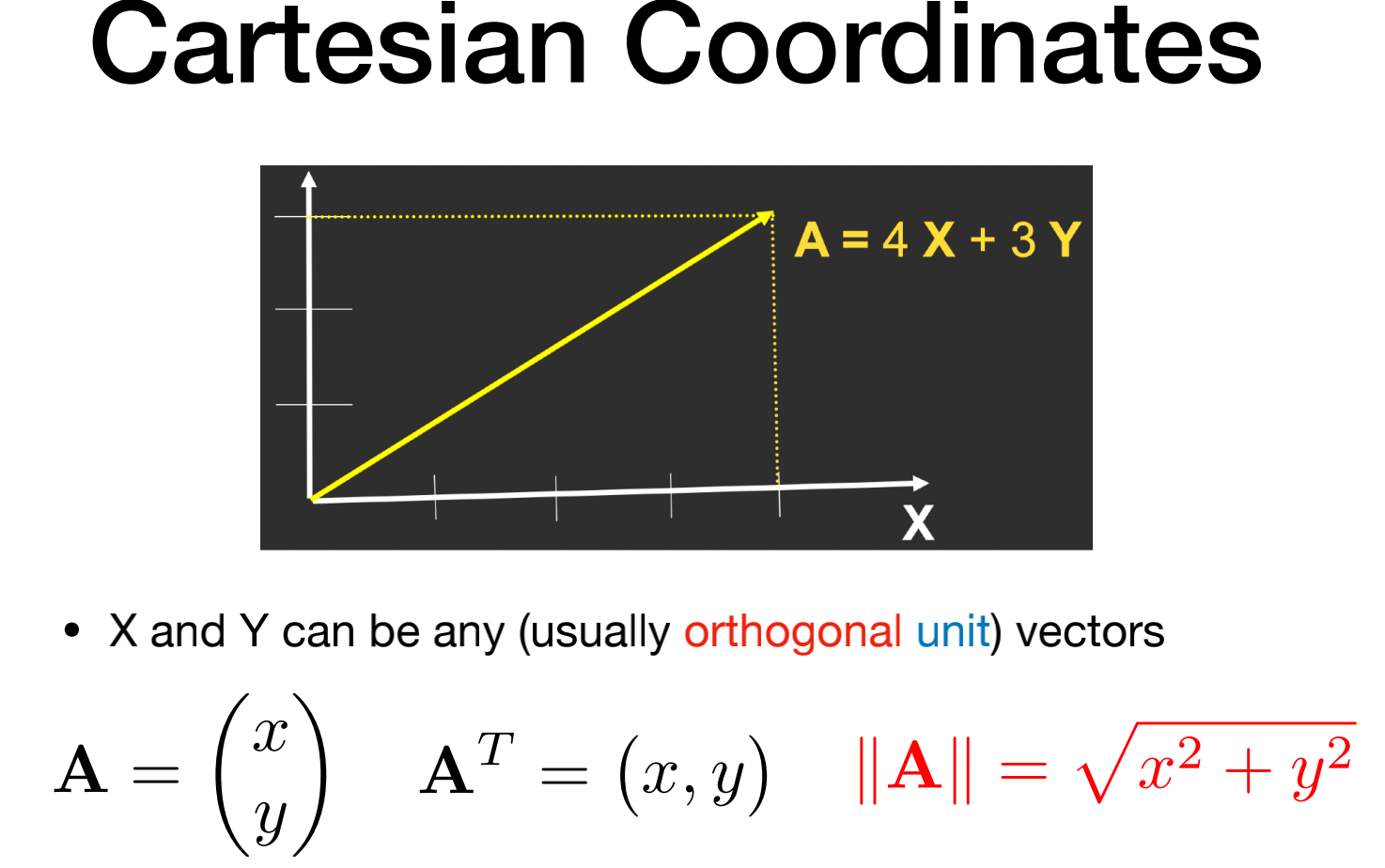
向量点乘：

可以通过点乘快速得到两个向量的夹角（特别是两个向量都是方向向量，点乘后直接得到夹角的余弦）

​​

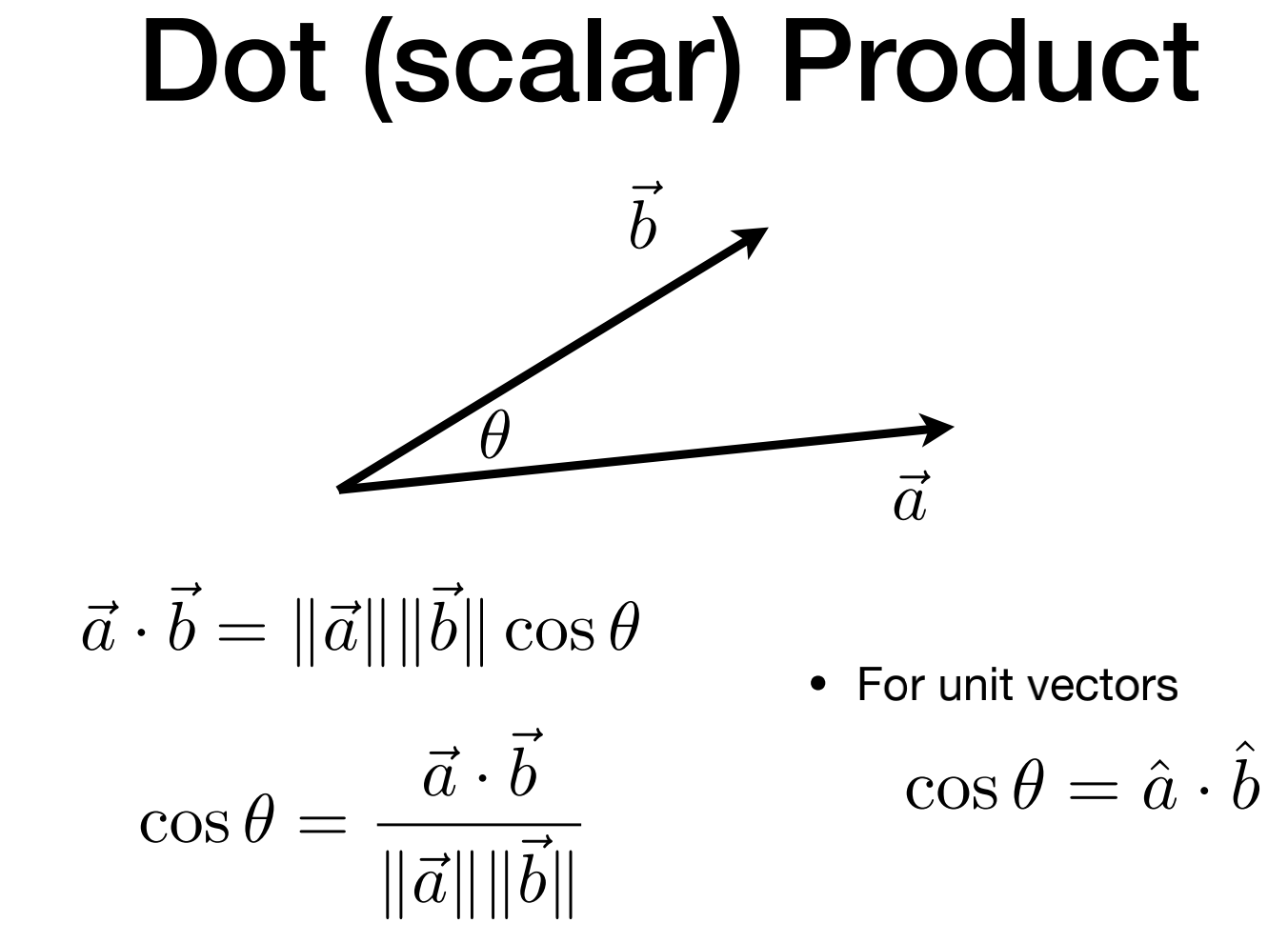
点乘运算满足交换律、分配律和结合律

​​

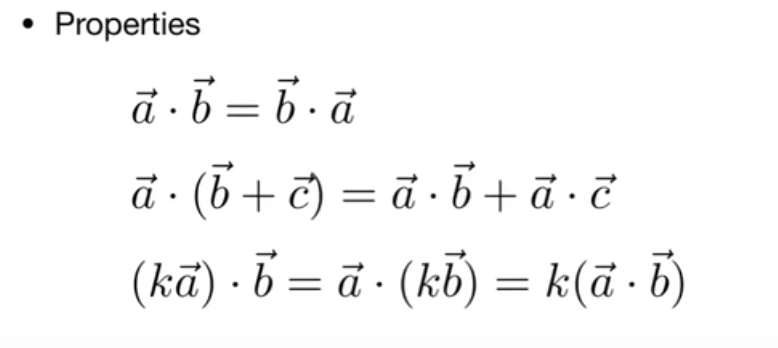
代数上的点乘即对应的坐标元素做乘积之后相加：

​​

点乘在图形学中的应用：

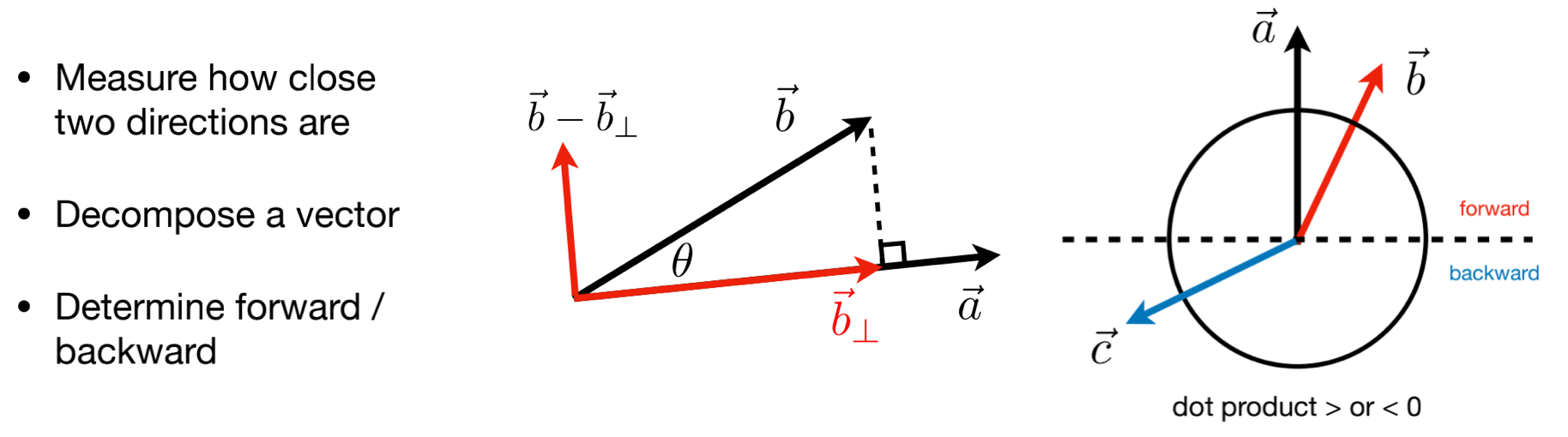
• 找到两个向量（两个方向）之间的夹角。比如光照模型，计算光照到物体表面的法线等等
• 找到一个向量到另一个向量上的投影，分解向量
• 计算两个向量之间有多接近：夹角越小（点乘的结果越大）越接近。比如镜面反射计算高光点
• 可以知道两个向量之间的方向是相同还是相反（正数相同、负数相反）
  ​​​​

向量叉乘

叉乘后的向量同时垂直于两个原向量，叉乘得到的向量方向符合右手螺旋定则。

​​

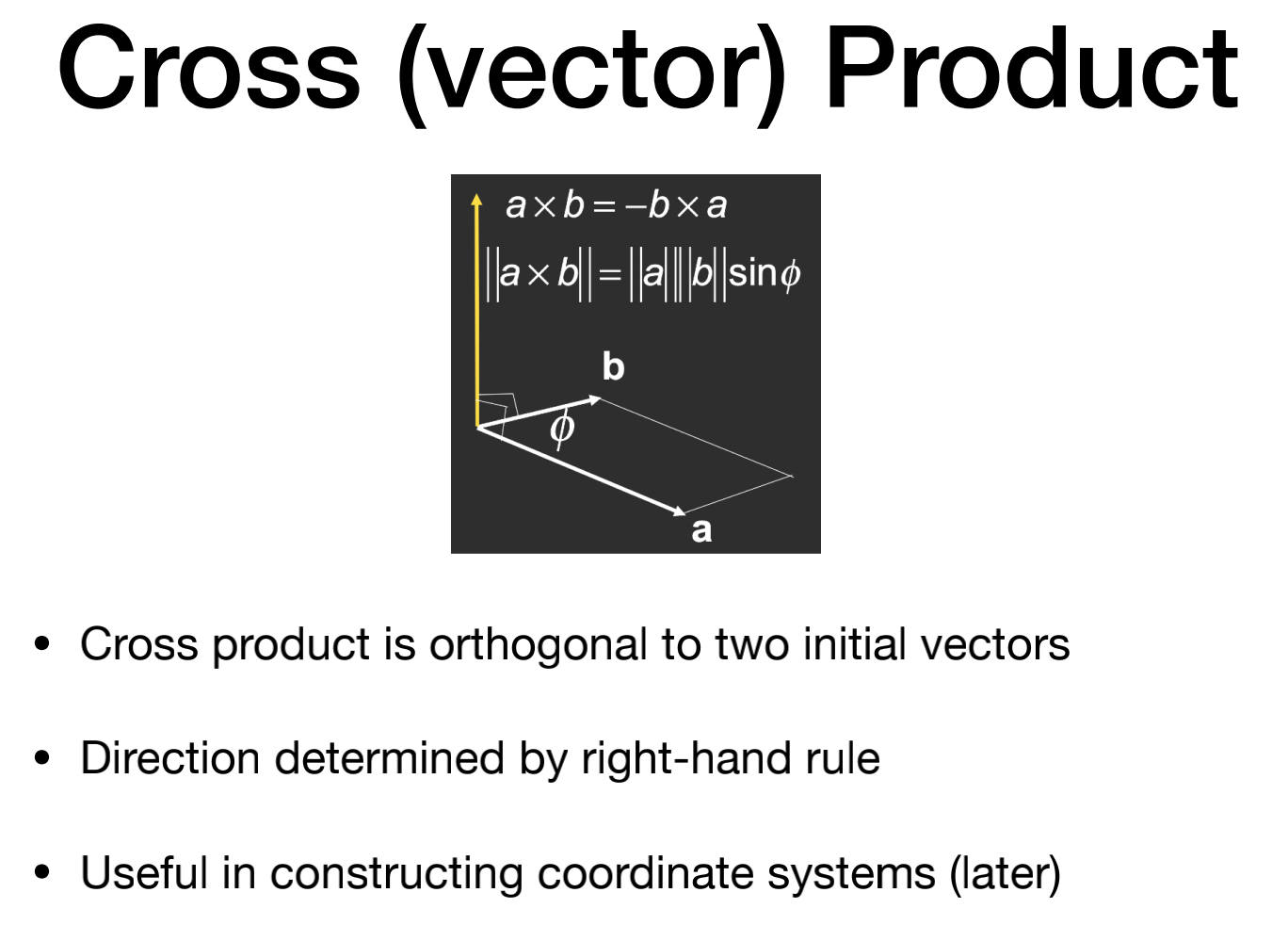
叉乘不满足交换律，需要加一个负号。但满足分配律和结合律。

​​

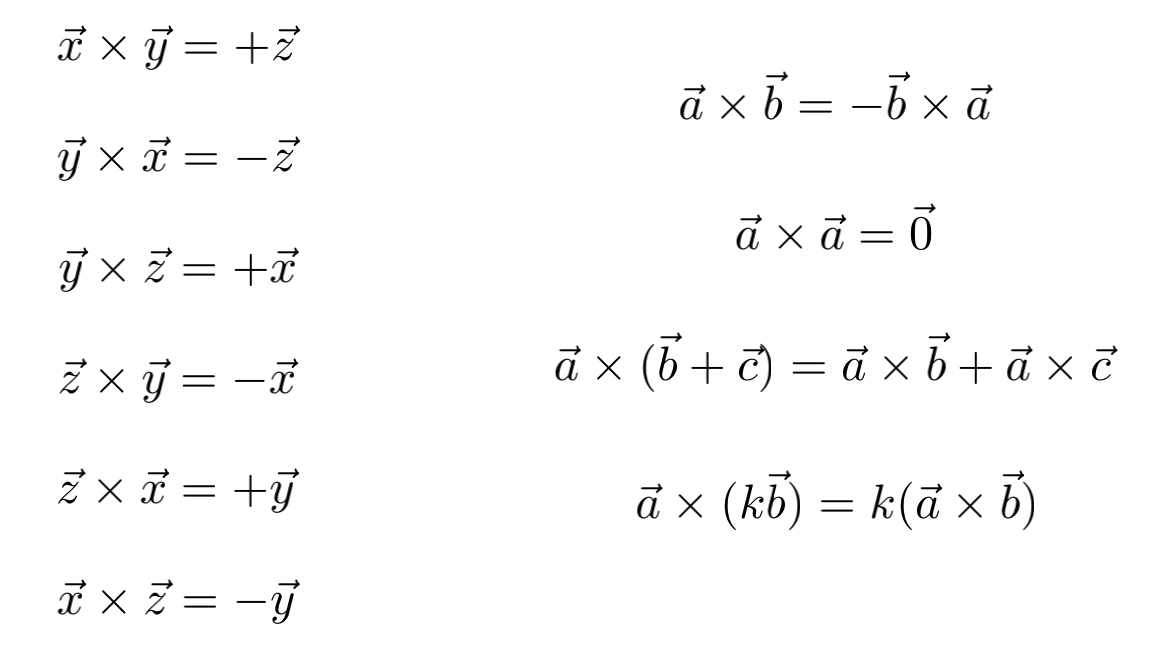
代数上：

​​​​

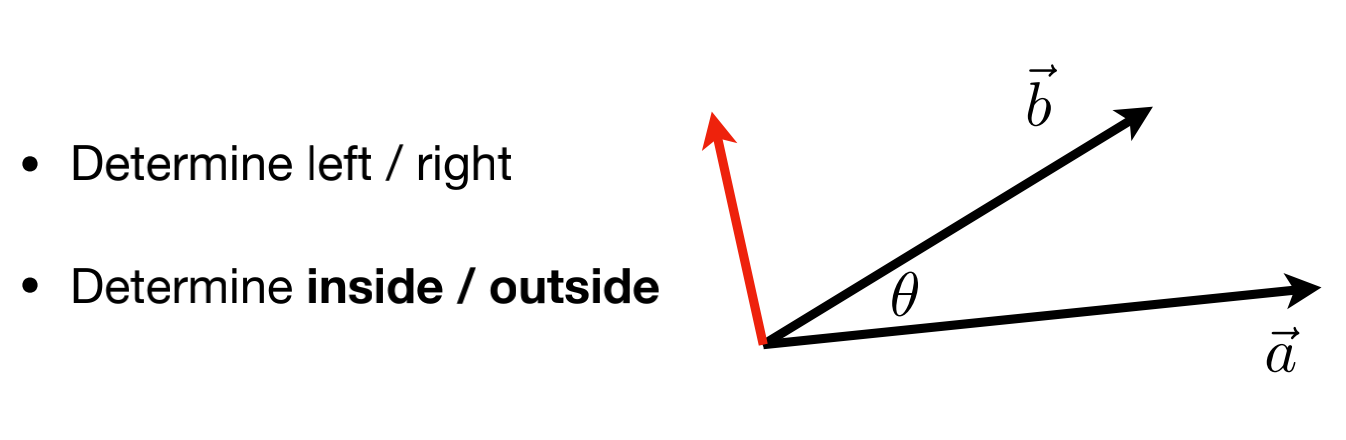
叉乘在图形学中的应用：

• 判定左和右

• 判定内和外（三角形光栅化的基础）

  ​​​​

3.矩阵（Matrics）

矩阵就是一堆数字，用 m 行 n 列的结构表示。

图形学中，用矩阵实现一些移动、旋转的变换。

​​

矩阵乘一个数就是把矩阵中每一个数字和该数字想乘得到一个矩阵。

矩阵乘积

一定要满足前一个矩阵的列数等于后一个矩阵的行数才能实现相乘。计算方式：乘出来的结果在 m 行 b 列就去找相乘的前一个矩阵的 m 行对应的值与后一个矩阵的 n 列对应的值一一相乘后再相加。

​​

矩阵不满足交换律，但满足结合率和分配律：

​​

矩阵和向量相乘：认为向量是一个 m 乘 1 的矩阵，则可以将任意一个 n 乘 m 的矩阵与向量相乘，基于该前提实现一个向量变换（比如相对一个坐标轴翻转）

​​

矩阵转置

​​

单位矩阵

单位矩阵只有对角线上有元素。

如果两个矩阵相乘为单位矩阵，则该两个矩阵互为逆矩阵。

​​

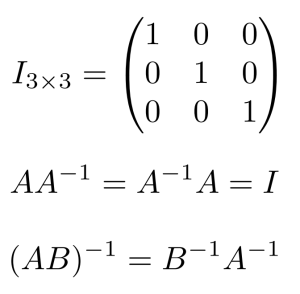
向量点乘和叉乘写成矩阵的形式（用在旋转的推导上）

​​